Lines and Angles NCERT Solutions | Mathematics for Class 6 PDF Download
Page 15
Figure it Out
Q1: 
Can you help Rihan and Sheetal find their answers?
Ans: We can draw an infinite number of lines passing through a single point, so Rihan can draw infinite lines through this point.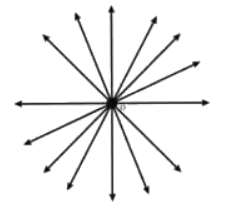
From two points, we can draw only 1 line passing through it, Sheetal can draw only 1 line through these two points.
Page 16
Q2: Name the line segments in Fig. 2.4. Which of the five marked points are on exactly one of the line segments? Which are on two of the line segments?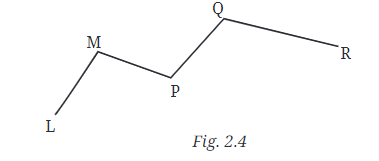 Ans:
Ans: 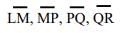
Points L and R are exactly on one line segment. Points M, P and Q are on two line segments.
Q3: Name the rays shown in Fig. 2.5. Is T the starting point of each of these rays?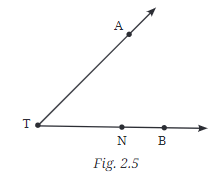
Ans: 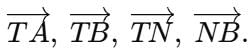 Here, T is the initial point for
Here, T is the initial point for 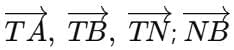 showing the arrow from N to B (so T is not the start of that one).
showing the arrow from N to B (so T is not the start of that one).
Q4: Draw a rough figure and write labels appropriately to illustrate each of the following:
(a)  meet at O.
meet at O.
Ans: 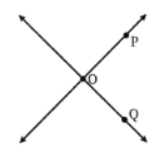
(b)  intersect at point M.
intersect at point M.
Ans: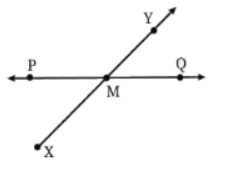
(c) Line I contains points E and F but not point D.
Ans: 
(d) Point P lies on AB.
Ans: 
Q5: In Fig. 2.6, name: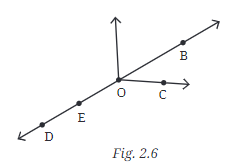
(a) Five points
Ans: The five points in the figure are D, E, O, C, and B.
(b) A line
Ans: 
(c) Four rays
Ans: 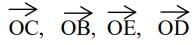
(d) Five line segments
Ans: The five line segments in the figure are .
.
Page 17
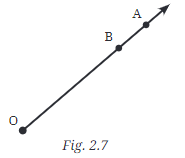
Q6: Here is a ray 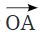 (Fig. 2.7). It starts at O and passes through the point A. It also passes through the point B.
(Fig. 2.7). It starts at O and passes through the point A. It also passes through the point B.
(a) Can you also name it as 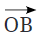 ? Why?
? Why?
Ans: Yes, the ray can also be named  because the ray OA passes through point B as well. Rays are named starting from the initial point and passing through any other point on the ray. Since the ray starts at O and passes through both B and A, it can be named
because the ray OA passes through point B as well. Rays are named starting from the initial point and passing through any other point on the ray. Since the ray starts at O and passes through both B and A, it can be named  .
.
(b) Can we write  ? Why or why not?
? Why or why not?
Ans: No, we cannot write 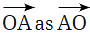 because rays are directional. The ray starts at point O and extends through A, so
because rays are directional. The ray starts at point O and extends through A, so  indicates the direction from O to A. Writing it as
indicates the direction from O to A. Writing it as  would imply the ray starts at A and goes towards O, which is incorrect in this context because O is the starting point.
would imply the ray starts at A and goes towards O, which is incorrect in this context because O is the starting point.
Page 17,18
Vidya has just opened her book. Let us observe her opening the cover of the book in different scenarios.
Q: Do you see angles being made in each of these cases? Can you mark their arms and vertex?
Ans: Yes, I can see the angles in each case. The arms of angles are marked with green colour and the vertices are marked with red dot in each case.
Page 19 & 20
Figure it Out
Q1: Can you find the angles in the given pictures? Draw the rays forming any one of the angles and name the vertex of the angle.
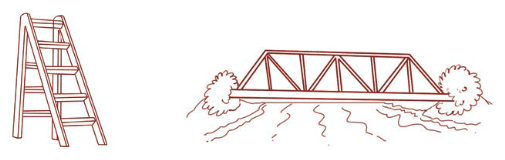 Ans:
Ans:
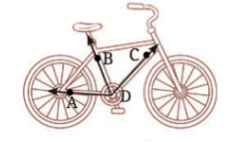 In ∠BDC, Rays are
In ∠BDC, Rays are  Vertex is D.
Vertex is D.
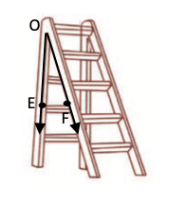
 In ∠POQ, Rays are
In ∠POQ, Rays are 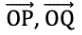 Vertex is O.
Vertex is O.
 In ∠EOF, Rays are
In ∠EOF, Rays are 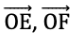 Vertex is O.
Vertex is O.
 In ∠ABC, Rays are
In ∠ABC, Rays are 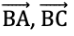 Vertex is B.
Vertex is B.
Q2: Draw and label an angle with arms ST and SR.
Ans: Arms of ∠RST are ST and SR.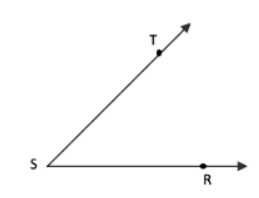 Steps:
Steps:
- First, draw a point S, which will be the vertex.
- Next, draw a ray starting at S and going in one direction. Label the other end T (making the ray ST).
- Then, draw another ray starting at S but going in a different direction. Label the other end R (making the ray SR).
- This forms an angle ∠TSR with S as the vertex, ST and SR as the arms.
Q3: Explain why ∠APC cannot be labelled as ∠P.
Ans: At P there are three angles.
∠P could mean ∠APB or ∠BPC or ∠APC.
To get the correct angle, it has to be named as ∠APC or ∠APB or ∠BPC.
Also note that a single point can not form an angle.
Q4: Name the angles marked in the given figure.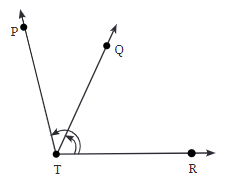
Ans: The angles marked in the figure are:
- ∠RTQ
- ∠RTP
Q5: Mark any three points on your paper that are not on one line. Label them A, B, C. Draw all possible lines going through pairs of these points. How many lines do you get? Name them. How many angles can you name using A, B, C? Write them down, and mark each of them with a curve as in Fig. 2.9.
Ans:  We get three lines
We get three lines  by joining pairs of these points.
by joining pairs of these points.
There are three angles ∠ABC, ∠ACB and ∠BAC formed using these points.
Page 21
Q6: Now mark any four points on your paper so that no three of them are on one line. Label them A, B, C, D. Draw all possible lines going through pairs of these points. How many lines do you get? Name them. How many angles can you name using A, B, C, D? Write them all down, and mark each of them with a curve as in Fig. 2.9.
Ans: 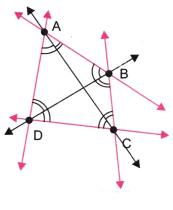 We get six lines
We get six lines  .
.
Also, we get twelve angles.
These are ∠BAC, ∠CAD, ∠BAD, ∠ABD, ∠DBC, ∠ABC, ∠BCA, ∠ACD, ∠BCD, ∠CDB, ∠CDA, ∠BDA.
Q: Is it always easy to compare two angles?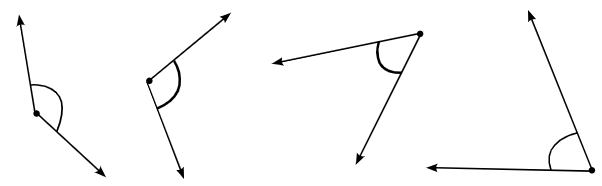
Here are some angles. Label each of the angles. How will you compare them?
Ans:
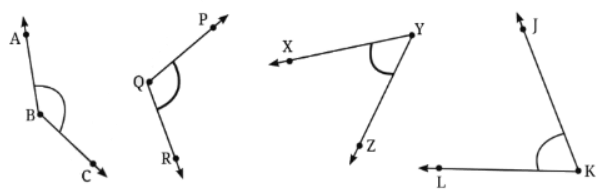
No it is not always easy to compare two angles. For eg, 89º & 91º angles cannot be compared without measuring or overlapping. But for the given figures, comparison is easy.
To compare the angles in the image, I will place one angle over the other by tracing or using transparent paper to directly compare which angle is larger or smaller. If I place one arm of each angle one over another, it can be observed easily (by looking at the other arm) which one is smaller or greater. By using this method, I can accurately compare the angles in the figure.Page 23
Q: Where else do we use superimposition to compare?
Ans: Superimposition is commonly used in situations in real-life objects like Scissors, compasses or other tools that involve angles. We can superimpose angles formed by these objects (e.g., the angle between the blades of a pair of scissors) to compare which angle is larger or smaller.
Figure it Out
Q1: Fold a rectangular sheet of paper, then draw a line along the fold created. Name and compare the angles formed between the fold and the sides of the paper. Make different angles by folding a rectangular sheet of paper and compare the angles. Which is the largest and smallest angle you made?
Ans: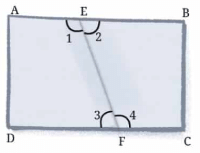
The angles formed with the line along the fold are ∠AEF, ∠BEF, ∠DFE and ∠CFE, which are marked with 1, 2, 3 and 4. Out of these angles, ∠AEF and ∠CFE are the larger ones, whereas ∠BEF and ∠DFE are the smaller ones.
Q2: In each case, determine which angle is greater and why.
(a) ∠AOB or ∠XOY
(b) ∠AOB or ∠XOB
(c) ∠XOB or ∠XOC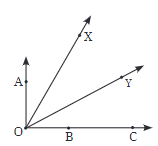
Discuss with your friends how you decided which one is greater.
Ans: (a) ∠AOB > ∠XOY, because ∠XOY is contained in ∠AOB. It means ∠XOY is a part of ∠AOB.
(b) ∠AOB > ∠XOB, because ∠XOB is contained in ∠AOB. It means ∠XOB is a part of ∠AOB.
(c) ∠XOB = ∠XOC, because both angles are formed with the same rays.
Q3: Which angle is greater: ∠XOY or ∠AOB? Give reasons.
Ans: ∠XOB > ∠AOB, because ∠AOB is contained in ∠XOB. It means ∠AOB is a part of ∠XOB.
Page 28
Let us consider a straight angle ∠AOB. Observe that any ray  divides it into two angles, ∠AOC and ∠COB.
divides it into two angles, ∠AOC and ∠COB.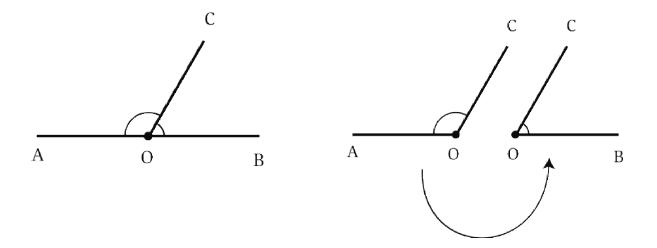
Q: Is it possible to draw 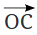 such that the two angles are equal to each other in size?
such that the two angles are equal to each other in size?
Ans: If the ray 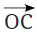 become perpendicular to AB, the two angles become equal to each other.
become perpendicular to AB, the two angles become equal to each other.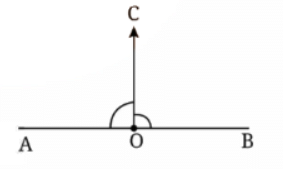
Page 29
Q: If a straight angle is formed by half of a full turn, how much of a full turn will form a right angle?
Ans: If a straight angle is formed by half of a full turn, a right angle is formed by one-quarter (1/4) of a full turn.
Steps of conclusion:
- A full turn is 360 degrees.
- A straight angle is half of a full turn, so it measures 180 degrees.
- A right angle is half of a straight angle, so it measures 90 degrees, which is one-quarter of a full 360-degree turn.
Figure it Out
Q1: How many right angles do the windows of your classroom contain? Do you see other right angles in your classroom?
Ans: A window has 4 right angles.
∠1, ∠2, ∠3 and ∠4.
Yes. At the corners of the door. At the corners of the blackboard, etc.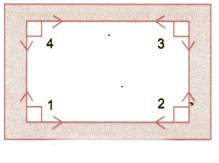
Page 30 & 31
Q2: Join A to other grid points in the figure by a straight line to get a straight angle. What are all the different ways of doing it?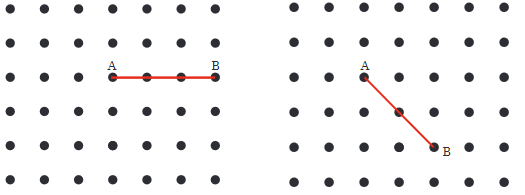
Ans: The different ways to form a straight angle:
This can be done in one way.
Q3: Now join A to the other grid points in the figure by a straight line to get a right angle. What are all the different ways of doing it?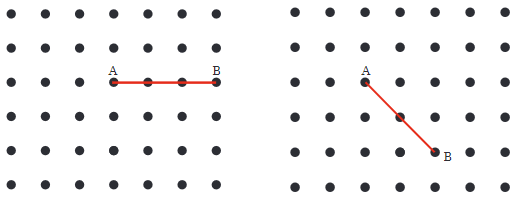 Hint: Extend the line further as shown in the figure below. To get a right angle at A, we need to draw a line through it that divides the straight angle CAB into two equal parts.
Hint: Extend the line further as shown in the figure below. To get a right angle at A, we need to draw a line through it that divides the straight angle CAB into two equal parts.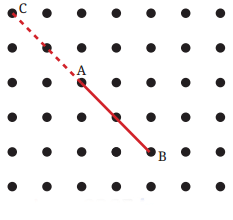 Ans:
Ans: 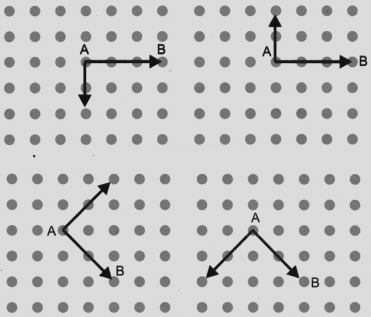
Q4: Get a slanting crease on the paper. Now, try to get another crease that is perpendicular to the slanting crease.
(a) How many right angles do you have now? Justify why the angles are exact right angles.
Ans: We get four right angles.
Let P be the point of intersection of the two creases.
The two creases are perpendicular lines meeting at P.
Hence, all four angles are right angles.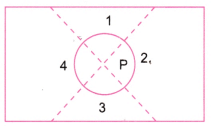 (b) Describe how you folded the paper so that any other person who doesn’t know the process can simply follow your description to get the right angle.
(b) Describe how you folded the paper so that any other person who doesn’t know the process can simply follow your description to get the right angle.
Ans: 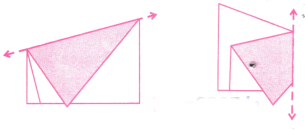
Step 1. Take a sheet of paper and fold it.
Step 2. Crease the fold.
Step 3. Now, again fold the paper so that the two parts of the crease coincide.
Step 4. Crease the fold.
Step 5. Unfold both the creases.
We get two perpendicular lines and four right angles as shown above.
Figure it Out
Q1: Identify acute, right, obtuse, and straight angles in the previous figures.
Ans: 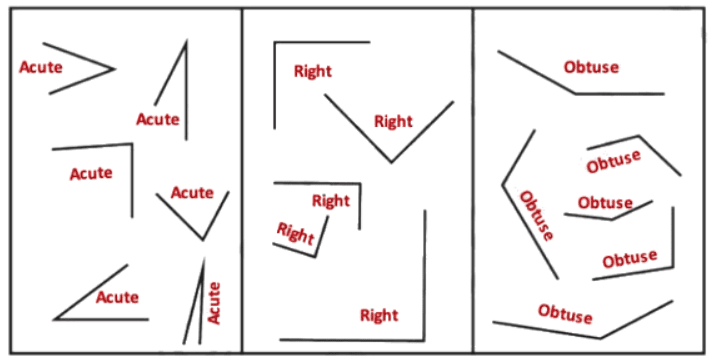
Q2: Make a few acute angles and a few obtuse angles. Draw them in different orientations.
Ans: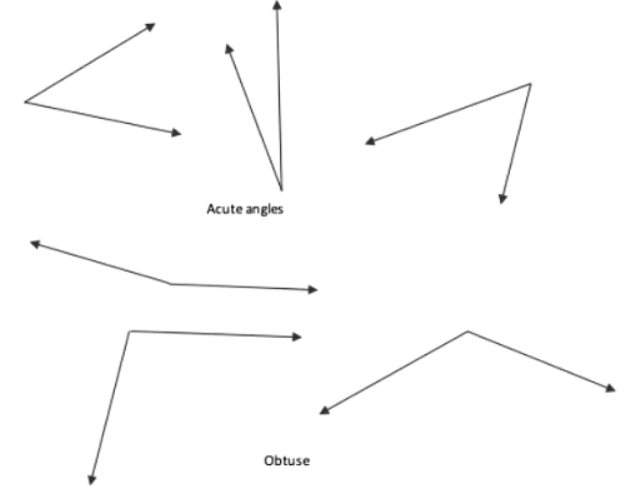
Page 32
Q3: Do you know what the words acute and obtuse mean? Acute means sharp and obtuse means blunt. Why do you think these words have been chosen?
Ans: Word ‘acute’ means ‘sharp’. The vertex of the angle appears as a sharp tip.
Word ‘obtuse’ means ‘blunt’. The vertex of the angle appears as a blunt tip.
Q4: Find out the number of acute angles in each of the figures below.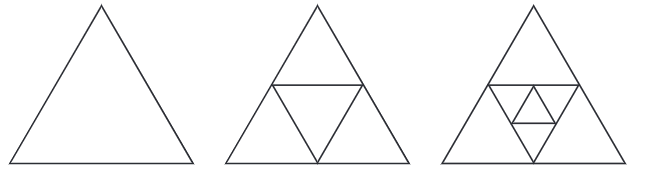 What will be the next figure and how many acute angles will it have? Do you notice any pattern in the numbers?
What will be the next figure and how many acute angles will it have? Do you notice any pattern in the numbers?
Ans: 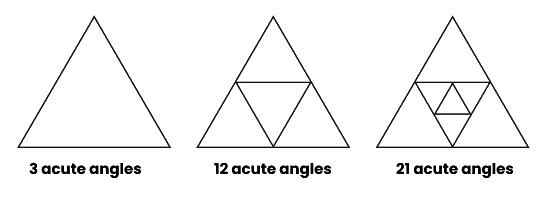
3 + 9=12
12 + 9 = 21
In every step, the numbers of angles increases by 9.
Next figure will be as follows: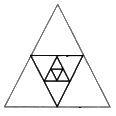 Number of acute angles = 21 + 9 = 30
Number of acute angles = 21 + 9 = 30
Page 33
Q: What is the measure of a straight angle in degrees? A straight angle is half of a full turn. As a full-turn is 360º, a half turn is 180º. What is the measure of a right angle in degrees? Two right angles together form a straight angle. As a straight angle measures 180º, a right angle measures 90º.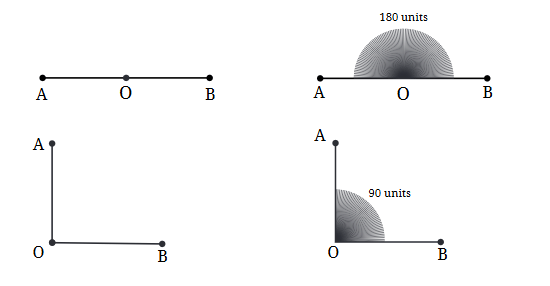 Ans: The measure of a straight angle in degrees is 180º and the measure of a right angle in degrees is 90º.
Ans: The measure of a straight angle in degrees is 180º and the measure of a right angle in degrees is 90º.
Page 34
Q: The circle has been divided into 1, 2, 3, 4, 5, 6, 8, 9 10 and 12 parts below. What are the degree measures of the resulting angles? Write the degree measures down near the indicated angles.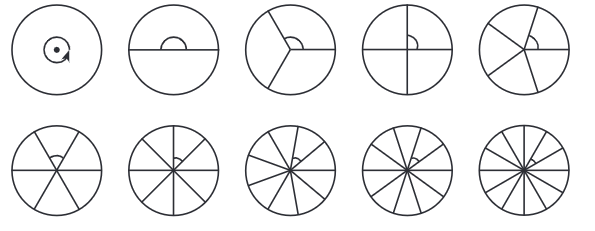 Ans:
Ans: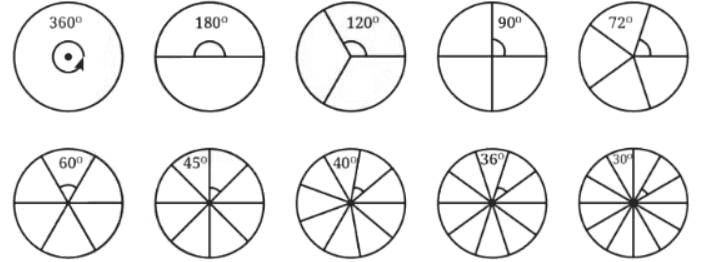
Page 35
Figure it out
Q: Write the measures of the following angles: 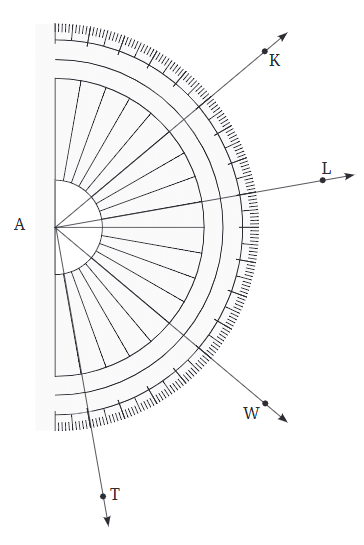 (a) ∠KAL
(a) ∠KAL
Notice that the vertex of this angle coincides with the centre of the protractor. So the number of units of 1 degree angle between KA and AL gives the measure of ∠KAL. By counting, we get ∠KAL = 30°. Making use of the medium sized and large sized marks, is it possible to count the number of units in 5s or 10s?
(b) ∠WAL
(c) ∠TAK
Ans:
(a) ∠KAL = 30º
(b) ∠WAL = 50º
(c) ∠TAK = 120º
Page 36 & 37
Q: Name the different angles in the figure and write their measures.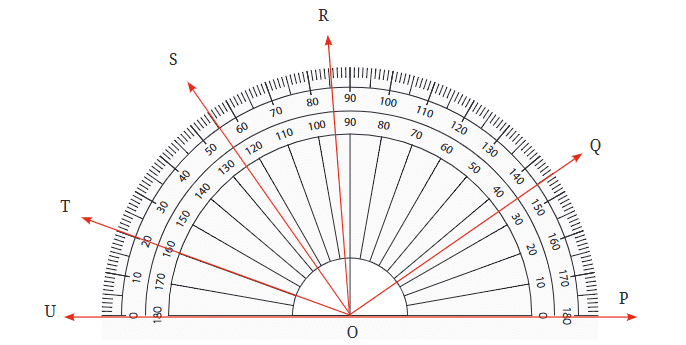 Did you include angles such as ∠TOQ?
Did you include angles such as ∠TOQ?
Which set of markings did you use - inner or outer?
What is the measure of ∠TOS?
Ans: 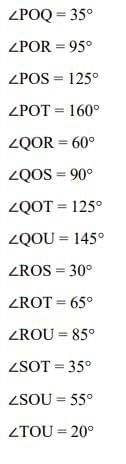
Yes, I have included angles such as ∠TOQ. I have used both set of markings - inner and outer, depending on angles. The mesure of ∠TOS = 35º.
Page 40
Think
Q: In Figure, we have ∠AOB = ∠BOC = ∠COD = ∠DOE = ∠EOF = ∠FOG = ∠GOH = ∠HOI = ____ Why?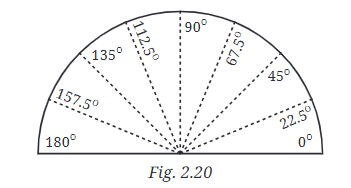 Ans: ∠AOB = ∠BOC = ∠COD = ∠DOE = ∠EOF = ∠FOG = ∠GOH = ∠HOI = 22.5º.
Ans: ∠AOB = ∠BOC = ∠COD = ∠DOE = ∠EOF = ∠FOG = ∠GOH = ∠HOI = 22.5º.
The straight angle is divided into 8 equal parts, that is why, the measure of each angle is 180º/8 = 22.5º.
Figure it out
Q1: Find the degree measures of the following angles using your protractor.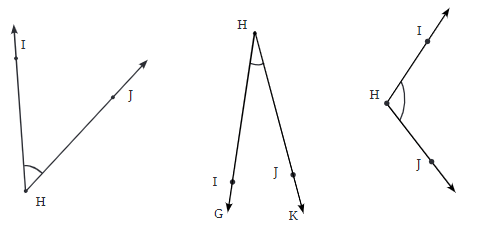
Ans: (a) ∠IHJ = 47°
(b) ∠IHJ = 23°
(c) ∠IHJ =108°
Q2: Find the degree measures of different angles in your classroom using your protractor.
Ans: Angle at the corner of the blackboard = 90°
Angle at the corner of the desk = 90°
Page 41
Q3: Find the degree measures for the angles given below. Check if your paper protractor can be used here!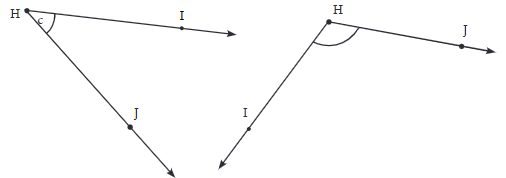 Ans: (a) ∠IHJ = 42°
Ans: (a) ∠IHJ = 42°
(b) ∠IHJ =116°
A paper protractor cannot be used here.
Q4: How can you find the degree measure of the angle given below using a protractor?
Ans: Measure of marked angle = 360º – Measure of unmarked angle = 360º - 100º = 260º
Q5: Measure and write the degree measures for each of the following angles:
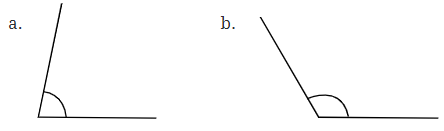
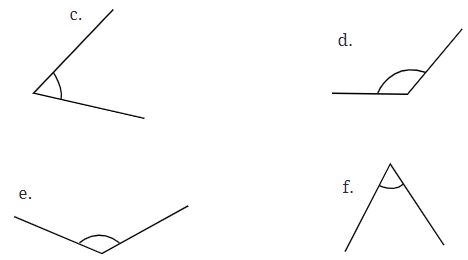
Ans: (a) Measure of given angle is 80°
(b) Measure of given angle is 120°
(c) Measure of given angle is 60°
(d) Measure of given angle is 130°
(e) Measure of given angle is 130°
(f) Measure of given angle is 60°
Page 42
Q6: Find the degree measures of ∠BXE, ∠CXE, ∠AXB, and ∠BXC.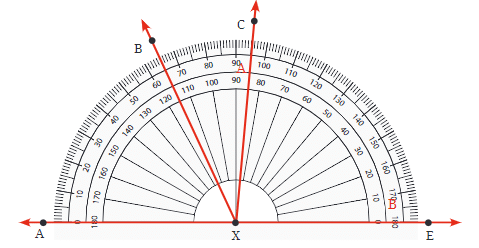
Ans: (a) ∠BXE =115°
(b) ∠CXE = 85°
(c) ∠AXB = 65°
(d) ∠BXC = 30°
Q7: Find the degree measures of ∠PQR, ∠PQS, and ∠PQT.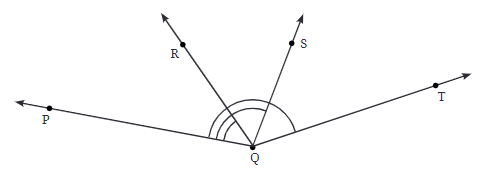
Ans: (a) ∠PQR = 45°
(b) ∠PQS = 100°
(c) ∠PQT = 150°
Page 43
Q8: Make the paper craft as per the given instructions. Then, unfold and open the paper fully. Draw lines on the creases made and measure the angles formed.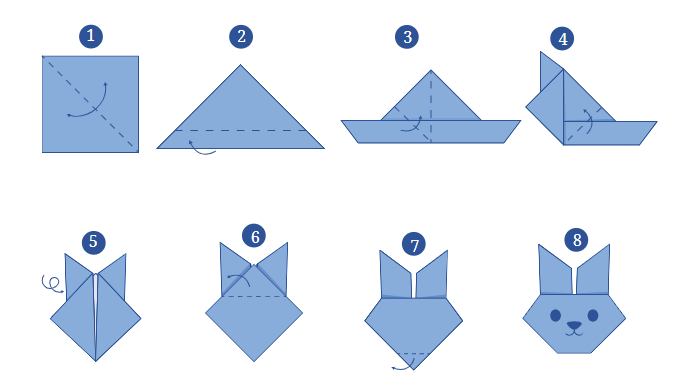
Ans: Step 1: When we fold the square paper diagonally, we create two right angles (90º) at the bottom corners and a 45º angle at the top.
Step 2: After folding, the base Of the triangle is flat, forming 90º angles at the bottom corners, while the top vertex remains 45º.
Step 3: When we fold the base upwards, we create a small right angle (90º) at the corner where the base meets the triangle.
Step 4: Folding in the sides to form the ears creates acute angles near the top, likely around 30º to 45º.
Step 5: As we further fold the sides inwards, the angles in the triangular ears might get sharper, leaving acute angles close to 30º at the tips of the ears.
Step 6: The fold upwards creates another acute angle at the tip of the bunny's face, likely around 45º.
Step 7: The final fold sharpens the bottom, maintaining the 90º at the base and 45º to 60º near the ears.
Step 8: In the complete bunny face, we will have multiple angles:
The ears form acute angles (around 30º to 45º).
The face near the chin forms an obtuse angle, close to 120º.
The sides of the face are around 90º to 120º depending on the precision of the folds.
Q9: Measure all three angles of the triangle shown in Fig. 2.21 (a), and write the measures down near the respective angles. Now add up the three measures. What do you get? Do the same for the triangles in Fig. 2.21 (b) and (c). Try it for other triangles as well, and then make a conjecture for what happens in general!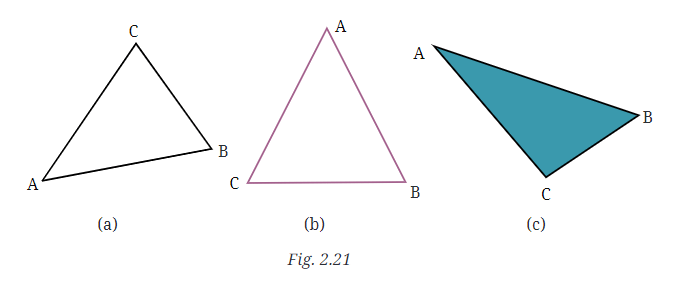
Ans:  (a) ∠ACB = 70º ; ∠CAB = 45º ; ∠ABC= 65º
(a) ∠ACB = 70º ; ∠CAB = 45º ; ∠ABC= 65º
Sum of all angles of ΔABC = ∠ACB + ∠CAB + ∠ABC
= 70º + 45º + 65º
= 180º
(b) ∠ACB = 62º ; ∠CAB = 55º ; ∠ABC= 63º
Sum of all angles of ΔABC = ∠ACB + ∠CAB + ∠ABC
= 62º + 55º + 63º
= 180º
(c) ∠ACB = 97º ; ∠CAB = 30º ; ∠ABC = 53º
Sum of all angles of ΔABC = ∠ACB + ∠CAB + ∠ABC
= 97º + 30º + 53º
= 180º
We have conjectured from the given activity that the sum of all the angles of any given triangle is always 180º.
Page 45
Figure it Out
Where are the angles?
Q1: Angles in a clock:
(a) The hands of a clock make different angles at different times. At 1 o’clock, the angle between the hands is 30°. Why?
(b) What will be the angle at 2 o’clock? And at 4 o’clock? 6 o’clock?
(c) Explore other angles made by the hands of a clock.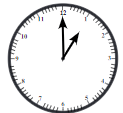
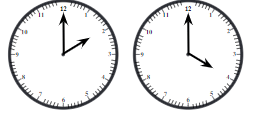
Ans: (a) Numbers 1 to 12 are written along the circumference of a clock at equal distances.
360 ÷ 12 = 30.
Hence, the angle between two consecutive numbers is 30°
At 1°’ o'clock hands are at 0 and 1 (consecutive numbers)
Hence angle between them is 30°.
(b) Angle between hands at 2 o’ clock = 2 × 30° = 60° angle between hands at 4 o’clock = 4 × 30°= 120°
Angle between hands at 6 o’ clock = 6 × 30°= 180°
(c) Angle between hands at 5 o’clock = 5 × 30°= 150°
Angle between hands at 7 o’ clock = 7 × 30° = 210°
Angle between hands at 8 o’ clock = 8 × 30° = 240°
Q2: The angle of a door: Is it possible to express the amount by which a door is opened using an angle? What will be the vertex of the angle and what will be the arms of the angle? Ans: Yes, it is possible to express the amount by which a door is opened by using an angle. The hinge of the door will be the vertex of the angle. The wall and the door will be the arms of the angle.
Ans: Yes, it is possible to express the amount by which a door is opened by using an angle. The hinge of the door will be the vertex of the angle. The wall and the door will be the arms of the angle.
Q3: Vidya is enjoying her time on the swing. She notices that the greater the angle with which she starts the swinging, the greater is the speed she achieves on her swing. But where is the angle? Are you able to see any angle? Ans:
Ans: 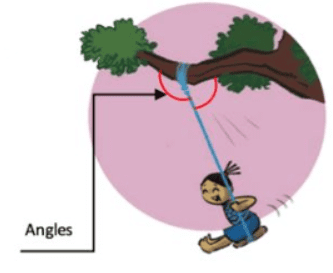
Student may not see the angle, but when the starting arm is fixed as the position where she starts swinging. The angle can be thought to be between positions where she starts the swinging (the initial position) and the position where she attains the greatest position of the swing at any one side.
Page 46
Q4: Here is a toy with slanting slabs attached to its sides; the greater the angles or slopes of the slabs, the faster the balls roll. Can angles be used to describe the slopes of the slabs? What are the arms of each angle? Which arm is visible and which is not? Ans:
Ans: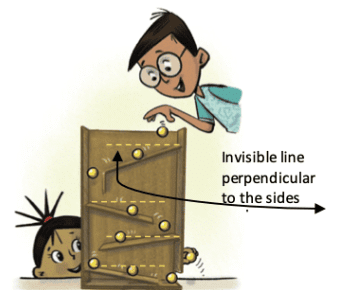 Yes, angles can be used directly to describe slopes of the slab, larger the angle, greater the slope of the slab. For each angle, one arm is a side and one arm is the slope. The vertical arm is not visible, whereas the other arm is visible. Here in this toy, edges of the slabs are the arms of the angles. Top horizontal ray is not visible, other arms in the form of edges of the slab are visible.
Yes, angles can be used directly to describe slopes of the slab, larger the angle, greater the slope of the slab. For each angle, one arm is a side and one arm is the slope. The vertical arm is not visible, whereas the other arm is visible. Here in this toy, edges of the slabs are the arms of the angles. Top horizontal ray is not visible, other arms in the form of edges of the slab are visible.
Q5: Observe the images below where there is an insect and its rotated version. Can angles be used to describe the amount of rotation? How? What will be the arms of the angle and the vertex?
Hint: Observe the horizontal line touching the insects. Ans: Yes, angles can be used to describe the amount of rotation by observing the initial and the final position of the insect.
Ans: Yes, angles can be used to describe the amount of rotation by observing the initial and the final position of the insect.
The horizontal line and the insect itself will be the arms of the angle. The vertex will be the back end of the insect.
Page 49
Figure it Out
Q1: In Fig. 2.23, list all the angles possible. Did you find them all? Now, guess the measures of all the angles. Then, measure the angles with a protractor. Record all your numbers in a table. See how close your guesses are to the actual measures.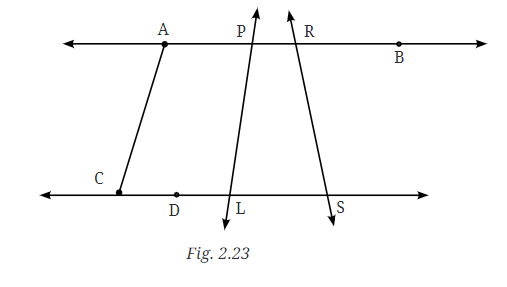 Ans: The given figure has 20 angles.
Ans: The given figure has 20 angles.
Guess: ∠1 = ∠4 = 60°; ∠2 = ∠3 = 120° by actual measure: ∠1 = ∠4 = 70°; ∠2 = ∠3 = 110°.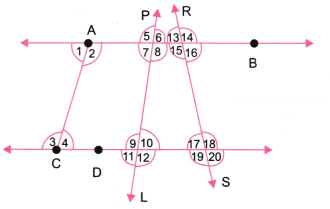 The guessed measurements were quite close to the actual measurements.
The guessed measurements were quite close to the actual measurements.
Page 50
Q2: Use a protractor to draw angles having the following degree measures:
(a) 110º
(b) 40º
(c) 75º
(d) 112º
(e) 134º
Ans: 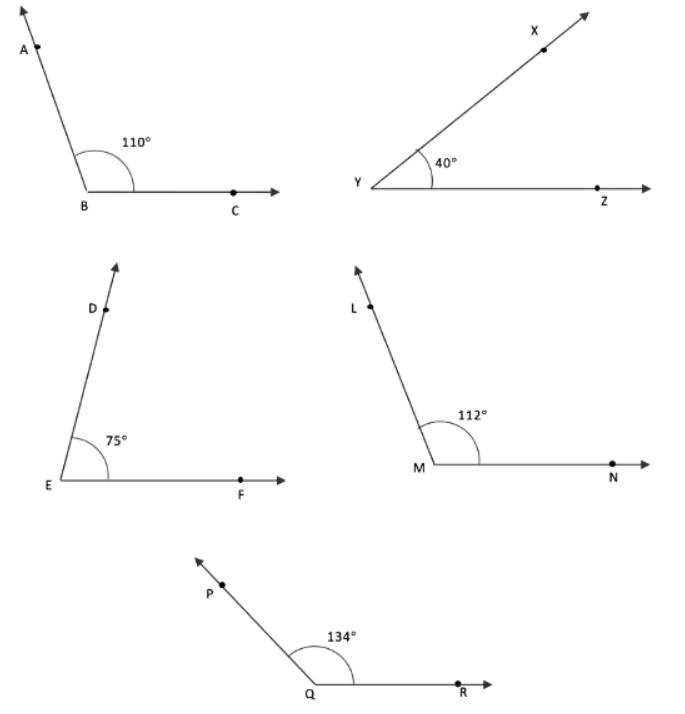
Q3: Draw an angle whose degree measure is the same as the angle given below: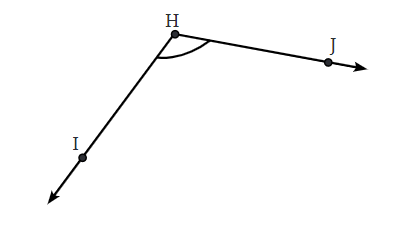 Also, write down the steps you followed to draw the angle.
Also, write down the steps you followed to draw the angle.
Ans: Step 1. Measure the given angle (∠IHJ = 120°)
Step 2. Using a protractor draw ∠ABC = 120°
Page 51 & 52
Figure it Out
Q1: In each of the below grids, join A to other grid points in the figure by a straight line to get:
(a) An acute angle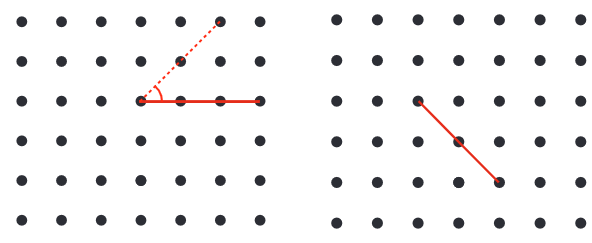 (b) An obtuse angle
(b) An obtuse angle (c) A reflex angle
(c) A reflex angle
Mark the intended angles with curves to specify the angles. One has been done for you.
Ans: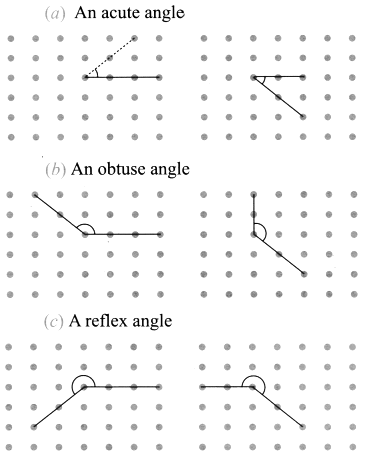
Q2: Use a protractor to find the measure of each angle. Then classify each angle as acute, obtuse, right, or reflex.
(a) ∠PTR
(b) ∠PTQ
(c) ∠PTW
(d) ∠WTP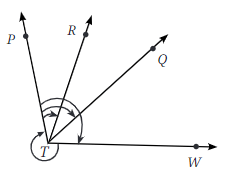
Ans:
(a) ∠PTR = 30° acute
(b) ∠PTQ = 60° acute
(c) ∠PTW = 102° obtuse
(d) ∠WTP = 258° reflex
Page 53
Let’s Explore:
Q: In this figure, ∠TER = 80º. What is the measure of ∠BET? What is the measure of ∠SET?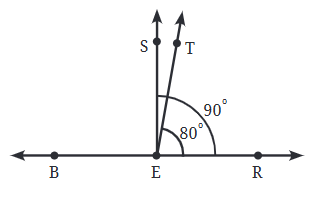 Ans: ∠BET = 180º -∠TER
Ans: ∠BET = 180º -∠TER
= 180º - 80º
= 100º
∠SET = ∠SER- ∠TER
= 90º - 80º
= 10º
Figure it Out
Q1: Draw angles with the following degree measures:
(a) 140°
(b) 82°
(c) 195°
(d) 70°
(e) 35°
Ans: 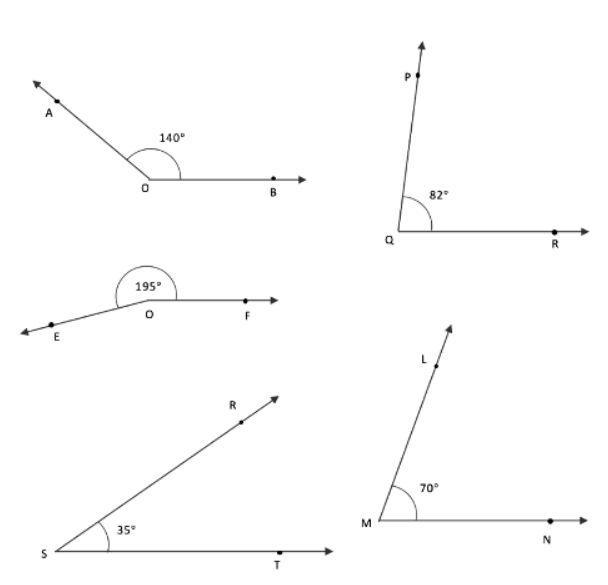
Q2: Estimate the size of each angle and then measure it with a protractor: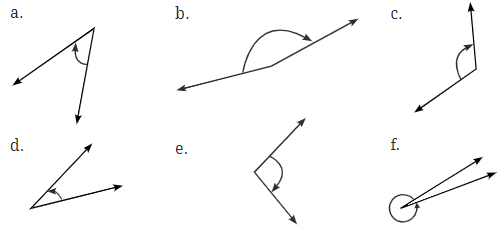 Classify these angles as acute, right, obtuse or reflex angles.
Classify these angles as acute, right, obtuse or reflex angles.
Ans: (a) 45° acute
(b) 150° obtuse
(c) 120° obtuse
(d) 30° acute
(e) 95° obtuse
(f) 350° reflex
Q3: Make any figure with three acute angles, one right angle and two obtuse angles.
Ans: 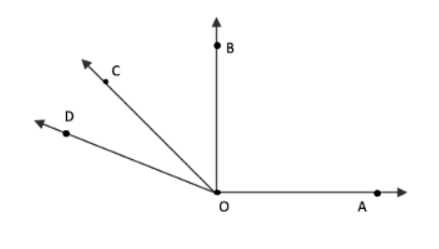 3 Acute angles = ∠COD, ∠BOC, ∠BOD
3 Acute angles = ∠COD, ∠BOC, ∠BOD
1 Right angle = ∠AOB
2 Obtuse angles = ∠AOC, ∠AOD.
Q4: Draw the letter ‘M’ such that the angles on the sides are 40° each and the angle in the middle is 60°.
Ans: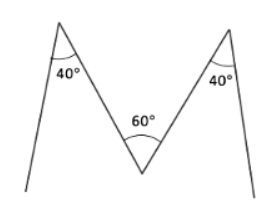
Explanation: Each side of the ‘M’ should form a 40° angle with the base, and the central angle at the top should be 60°.
Q5: Draw the letter ‘Y’ such that the three angles formed are 150°, 60° and 150°.
Ans: 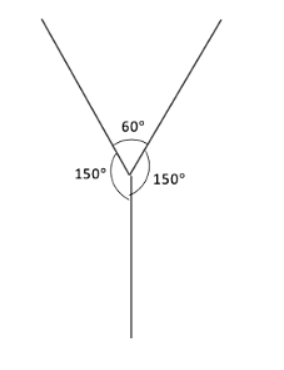
Explanation: The angles at the top should be wide (150°) while the central angle at the base should be narrower (60°).
Page 54
Q6: The Ashoka Chakra has 24 spokes. What is the degree measure of the angle between two spokes next to each other? What is the largest acute angle formed between two spokes? Ans: The Ashoka Chakra has 24 spokes and has a total of 360°.
Ans: The Ashoka Chakra has 24 spokes and has a total of 360°.
Angle between two spokes = 360°/24 = 15°
The possible angles between two spokes are 15°, 30°, 45°, 60°, 75°.
Therefore, the largest acute angle formed between two spokes is 75°.
Q7: Puzzle: I am an acute angle. If you double my measure, you get an acute angle. If you triple my measure, you will get an acute angle again. If you quadruple (four times) my measure, you will get an acute angle yet again! But if you multiply my measure by 5, you will get an obtuse angle. What are the possibilities for my measure?
Ans: Let the measure of the angle be m
Then 5 × m > 90 but 4 × m < 90
or m > 90/5 and m < 90/4
Hence m > 18 but m < 22 1/2
Hence measure of the angle is 19° or 20° or 21° or 22º.
|
48 videos|334 docs|23 tests
|
FAQs on Lines and Angles NCERT Solutions - Mathematics for Class 6
| 1. What are the different types of angles? |  |
| 2. How do you identify complementary angles? |  |
| 3. What is the sum of the angles in a triangle? |  |
| 4. How can you determine if two lines are parallel? |  |
| 5. How can you use the concept of alternate interior angles? |  |

















