Previous Year Questions: Context Free Grammar | Theory of Computation - Computer Science Engineering (CSE) PDF Download
Q1: Consider the following augmented grammar, which is to be parsed with a SLR parser. The set of terminals is {a, b, c, d, #, @}
S' → S
S → SS ∣ Aa ∣ bAc ∣ Bc ∣ bBa
A → d#
B → @
Let I0 = CLOSURE ({S' → •S}). The number of items in the set GOTO (I0, S) is ______ (2024 SET−2)
(a) 5
(b) 8
(c) 9
(d) 10
Ans: (c)
Sol: 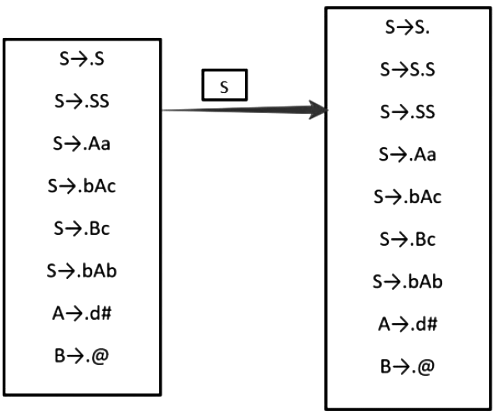
From above DFA we can see that Go to (closure (I0), S) contains 9 items
Q2: Consider a context-free grammar G with the following 3 rules.
S → aS, S → aSbS, S → c
Let w ∈ L(G). Let na(w), nb(w), nc(w) denote the number of times a, b, c occur in w, respectively. Which of the following statements is/are TRUE? (2024 SET−2)
(a) na(w) > nb(w)
(b) na(w) > nc(w) - 2
(c) nc(w) = nb(w) + 1
(d) nc(w) = nb(w) * 2
Ans: (b, c)
Sol:
The smallest string is "c". So option A and D are invalid. Number of a's = 0 and Number of c's = 1.
So as per option B 0>-1 which is true and same applies to other strings as well. Also number of b's in smallest string are 0 so option C is true as well and same is the case for other strings.
Q3: Consider the following context-free grammar where the start symbol is S and the set of terminals is {a, b, c, d}.
S → AaAb ∣ BbBa
A → cS ∣ ϵ
B → dS ∣ ϵ
The following is a partially-filled LL(1) parsing table.
Which one of the following options represents the CORRECT combination for the numbered cells in the parsing table?
Note: In the options, "blank" denotes that the corresponding cell is empty. (2024 SET−2)
(a) (1) S → AaAb (2) S → BbBa (3) A → ϵ (4) Β ϵ
(b) (1) S → BbBa (2) S → AaAb (3) A → ϵ (4) Β ϵ
(c) (1) S → AaAb (2) S → BbBa (3) blank (4) blank
(d) (1) S → BbBa (2) S → AaAb (3) blank (4) blank
Ans: (a)
Sol: To complete the given LL(1) table first we have to find the FIRST and FOLLOW of the given grammar, that is:
Now we can fill the entries in LL(1) table: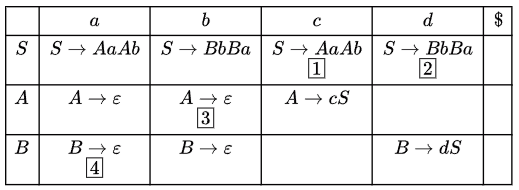
The correct Option is (A).
Q4: Let G = (V, Σ, S, P) be a context-free grammar in Chomsky Normal Form with ∑ = {a, b, c} and V containing 10 variable symbols including the start symbol S. The string w = a30b30c30 is derivable from S. The number of steps (application of rules) in the derivation S → w is _____ (2024 SET−1)
(a) 154
(b) 235
(c) 179
(d) 542
Ans: (c)
Sol:
For CNF, number of steps required is 2[w] - 1
Example: if
S -> AA
A -> a
for string 'aa' we will need
S -> AA -> Aa -> aa
(Thus number of steps to derive string is 3)
Here the [w] = 90
Thus the number of derivations will be 2*90 - 1 = 179
Answer: 179
Q5: Consider the context-free grammar G below
S → aSb ∣ X
X → aX ∣ Xb ∣ a ∣ b
where S and X are non-terminals, and a and b are terminal symbols. The starting non-terminal is S.
Which one of the following statements is CORRECT? (2023)
(a) The language generated by G is (a + b)*
(b) The language generated by G is a*(a + b)b*
(c) The language generated by G is a*b* (a + b)
(d) The language generated by G is not a regular language
Ans: (b)
Sol:
Given productions of grammar G:
S → aSb / X
X → aX / Xb / a / b
NOTE: While finding the expression for any given Grammar G, always try to solve in bottom up fashion.
For X: In X, any number of a & b can occur and when we wish to terminate, we have choice between a & b.
So, X → am (a + b)/(a + b)bp (m ≥ 0, p ≥ 0)
Replace this X in above productions. Then productions will look like this:
S → aSb/am (a + b)/(a + b)bp.
For S: Let's first analyze S → aSb
S → aSb
S → aaSbb
S → aaaSbbb
This is simply, anbn (n ≥ 1). Let's Substitute this:
S → anam (a + b)bn/an (a + b)bpbn
This can further be simplified as a*(a + b)b*
Option B, is correct answer.
Q6: Consider the following context-free grammar where the set of terminals is {a, b, c, d, f}.
S → d a T ∣ R f
T → a S ∣ b a T ∣ ϵ
R → c a T R ∣ ϵ
The following is a partially-filled LL(1) parsing table.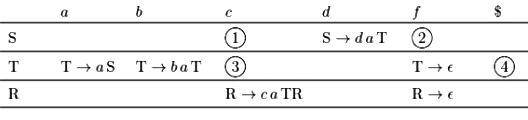
Which one of the following choices represents the correct combination for the numbered cells in the parsing table ("blank" denotes that the corresponding cell is empty)? (2021 SET−1)
(a) A
(b) B
(c) C
(d) D
Ans: (a)
Sol: 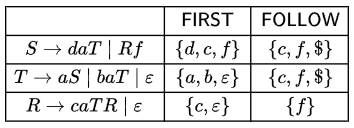
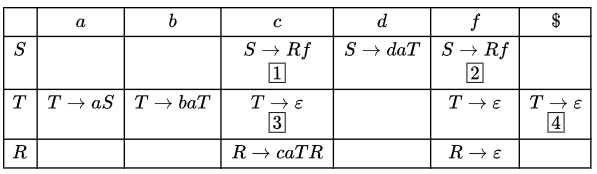
Ans: A (1) S → Rf (2) S → Rf (3) T → ϵ (4) T → ϵ
Q7: Consider the following expression grammar G:
E → E - T | T
T → T + F | F
F → (E) | id
Which of the following grammars is not left recursive, but is equivalent to G? (2017 SET−2)
(a)
E → E - T | T
T → T + F | F
F → (E) | id
(b)
E → TE'
E' → TE' | ∈
T → T + F | F
F → (E) id
(c)
E → TX
X →-TX | ∈
T → FY
Y → + FY | ∈
F → (E) | id
(d)
E → TX | (TX)
X → -TX | + TX | ∈
T → id
Ans: (c)
Sol:
Since, the grammar given in the question is left recursive, we need to remove left recursion ,
If Grammar is of form
A → Aa | β
then after removal of left recursion it should be written as
A → βA'
A' → aA' | ϵ
Since the grammar is:
E → E - T | T (Here a is ' -T' and β is T)
T → T + F | F (Here a is ' +F' and β is F)
F → (E) | id (It is not having left recursion)
Rewriting after removing left recursion :
E → TE'
E' → -TE' | ϵ
T → FT'
T' → +FT' | ϵ
F → (E) | id
Now replace E' with X and T' with Y to match with Option C.
E → TX
X → -TX | ϵ
T → FY
Y → +FY | ϵ
F → (E) | id
Hence C is correct.
Q8: Identify the language generated by the following grammar, where S is start variable. (2017 SET−2)
s → XY
X → aX | a
Y → aYb | ∈
(a) {ambn | m ≥ n, n > 0}
(b) {ambn | m ≥ n, n ≥ 0}
(c) {ambn | m > n, n ≥ 0}
(d) {ambn | m > n, n > 0}
Ans: (c)
Sol:
S → XY
X → aX | a
Y → aYb | ∈
X generates atleast one 'a'. While Y generates equal no of a's and b's(including epsilon).
L = {a, aa, aaa, aab, aaaa, aaab, aaaaa, aaabb,...}
Hence, answer should be Option C.
Q9: Which of the following statements about parser is/are CORRECT? (2017 SET−2)
I. Canonical LR is more powerful than SLR.
II. SLR is more powerful than LALR
III. SLR is more powerful than Canonical LR.
(a) I only
(b) II only
(c) III only
(d) II and III only
Ans: (a)
Sol: 
For a parser more power means it can parse more strings. So, here only the first statement is correct.
Correct Answer: A
Q10: If G is grammar with productions
S → SaS|aSb|bSa|SS∈
where S is the start variable, then which one of the following is not generated by G? (2017 SET−1)
(a) abab
(b) aaab
(c) abbaa
(d) babba
Ans: (d)
Sol:
S → SaS | aSb | bSa | SS | ∈
If we observe carefully the given grammar is generating all strings over ∑ = {a, b} having number of b's not exceeding the number of a's. So, we can straight away give answer as option D. Strings in other options can be generated as shown below.
A. abab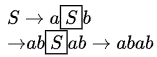
B. aab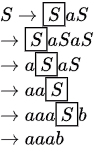
C. abbaa
Hence strings in options A, B and C can be generated using the given grammar but not the one in option D. Answer is D.
Q11: Consider the following grammar.
P → XQRS
Q → yz | z
R → W | ε
S → y
What is follow (Q) ? (2017 SET−1)
(a) {R}
(b) {In}
(c) {w, y}
(d) {W, $}
Ans: (c)
Sol:
Follow of Q is first of R so we get {w}
but since R can be Null so we have to check first of S which is {y}
So follow Q = {w, y}
Correct option (C)
Q12: Consider the following context-free grammar over the alphabet ∑ = {a, b, c} with S as the start symbol.
S → abScT | abcT
T → bT | b
Which one of the following represents the language generated by the above grammar ? (2017 SET−1)
(a) {(ab)n (cb)n | n ≥ 1}
(b)
(c) (ab)n (cbm)n | n, m ≥ 1
(d) (ab)n (cbn)m | n, m ≥ 1
Ans: (b)
Sol:
Consider the 1st production S→ abScT
This production generates equal number of (ab)'s and c's but after each c there is T which goes to T → bТ
So, with each c there can be one or more b's (one because of production T b and more because of T → bT)
and these b's are independent.
For example,
ababcbbcbb is the part of the language
and ababcbbbbbbcbb is also the part of the language so we can rule out options A and C as both say equal
number of b's after each c.
In option D equal number of (ab)'s and c's is not satisfied. The only option that satisfies these 2 conditions is
option B.
Q13: Which one of the following grammars is free from left recursion? (2016 SET−2)
(a) S → AB
A → Aa | b
B → c
(b) S → Ab| Bb| c
A → Bb | ε
B → e
(c) S → Aa | B
A → Bb | Sc | ε
B → d
(d) S → Aa | Bb | c
A → Bd | ε
B → Ae | ε
Ans: (b)
Sol:
Option (A) has immediate left recursion."A → Aa"
Option (C) has indirect left recursion
Option (D) has indirect left recursion
Option (B) is free from left recursion. No direct left recursion. No indirect left recursion.
Correct Option: B
Q14: Consider the following context-free grammars:
G1: S → aS B, B → b | bB
G2: S → aA | bB, A → aA | B | ε, B → bB | ε
Which one of the following pair of languages is generated by G1 and G2, respectively? (2016 SET−1)
(a) {ambn ∣ m > 0 or n > 0} and {ambn ∣ m > 0 and n > 0}
(b) {ambn ∣ m > 0 or n > 0} and {ambn ∣ m > 0 and n ≥ 0}
(c) {ambn ∣ m ≥ 0 or n > 0} and {ambn ∣ m > 0 and n > 0}
(d) {ambn ∣ m ≥ 0 and n > 0} and {ambn ∣ m 0 or n > 0}
Ans: (d)
Sol:
G1 results in strings b, ab, bb, aab, abb, bbb,... i.e. ambn, m ≥ 0 and n > 0 (and because only a's are not possible but only b's are)
G2 result in strings a, b, aa, ab, bb, aaa, aab, abb, bbb ... i.e. ambn, m > 0 or n > 0 (or because only b's is possible b, bb, bbb,, only a's are possible)
So, Answer is (D)
Q15: Which of the following languages is generated by the given grammar? (2016 SET−1)
S → aS | bS | ε
(a) {anbm | n, m ≥ 0}
(b) {{w ∈ {a, b}* | w has equal number of a's and b's}
(c) {an | n ≥ 0} ∪ {bn | n ≥ 0} ∪ {anbn ≥ 0}
(d) {a, b}*
Ans: (d)
Sol:
Correct Option: D
S → aS | bS | ε
is (a + b)*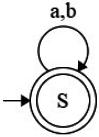
|
18 videos|93 docs|44 tests
|
FAQs on Previous Year Questions: Context Free Grammar - Theory of Computation - Computer Science Engineering (CSE)
| 1. What is a context-free grammar in computer science? |  |
| 2. How are context-free grammars used in parsing algorithms? |  |
| 3. What are some common applications of context-free grammars in computer science? |  |
| 4. Can context-free grammars generate all possible languages? |  |
| 5. How can one determine if a given string belongs to the language generated by a context-free grammar? |  |





















