Perimeter and Area Chapter Notes | Chapter Notes For Class 6 PDF Download
| Table of contents |

|
| Introduction |

|
| Perimeter |

|
| Area |

|
| Area of a Triangle |

|
| Key points |

|
Introduction
This chapter is all about perimeter and area—two important ways to understand shapes and the space they take up. The perimeter tells us how far it is around a shape, like measuring the length of a fence around a garden. The area tells us how much space is inside a shape, like figuring out how much paint is needed to cover a wall.
Learning these concepts will help you solve real-life problems, from designing playgrounds to decorating your room, and make you see math in the world around you.
Perimeter
- The perimeter of a closed plane figure is the total distance around its boundary when you go all the way around it once.
- For a polygon, which is a closed shape made up of straight line segments, the perimeter is simply the sum of the lengths of all its sides. This means you add up the lengths of each side to get the total distance around the outer edge of the shape.
- Perimeter of a polygon = Sum of the lengths of all its sides.
- The concept of the perimeter is widely used in real life. For Example:
- For fencing land.
- For building a compound wall around a house.

Perimeter of a Rectangle

- Perimeter of a rectangle = length + breadth + length + breadth.
- Perimeter of a rectangle = 2 x (length + breadth).
- The perimeter of a rectangle is twice the sum of its length and breadth.
Example: Imagine you have a rectangular garden. The garden is 12 cm long and 8 cm wide. You want to put a fence all around it. To find out how much fencing you need, you need to calculate the perimeter of the rectangle.
Solution: The perimeter is the total distance around the garden, which is the sum of all four sides. Here’s how you calculate it:
Step 1: Add the length and the width together.
- Length (AB) = 12 cm
- Width (BC) = 8 cm
- AB + BC = 12 cm + 8 cm = 20 cm
Step 2: Since the rectangle has two lengths and two widths, multiply the sum by 2.
- Perimeter = 2 × (Length + Width)
- Perimeter = 2 × 20 cm = 40 cm
So, the perimeter of the garden is 40 cm.
Perimeter of a Square
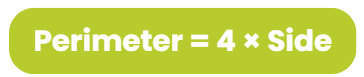
- Perimeter of a square = 4 x length of a side.
- The perimeter of a square is quadruple the length of its side.
Example: Debojeet has a square photo frame, and each side of the frame is 1 meter long. He wants to put colored tape all around the frame. To find out how much tape he needs, we calculate the perimeter of the square.
Solution: For a square, all four sides are the same length. The perimeter is simply four times the length of one side:
Step 1: Multiply the length of one side by 4.
- Perimeter = 4 × Side
- Perimeter = 4 × 1 m = 4 m
So, Debojeet needs 4 meters of tape to go around the photo frame.
Perimeter of a Triangle

Example: Let’s say you have a triangle with sides that are 4 cm, 5 cm, and 7 cm long. You want to know the perimeter of this triangle.
Solution: The perimeter is the sum of the lengths of all three sides:
- Perimeter = 4 cm + 5 cm + 7 cm = 16 cm
So, the perimeter of the triangle is 16 cm.
Perimeter of Shapes Created with Lines
The shapes of the letters "F" are created using lines on a grid. To find the perimeter of each letter, we need to measure the lengths of all the sides that make up the shape.
- Straight Lines (s): These are the lines that run either horizontally or vertically.
- Diagonal Lines (d): These are the lines that connect points diagonally, making a slanted line.
- You count the number of straight units (s) and diagonal units (d).
- Add these together to get the total perimeter in the form of "s + d units."
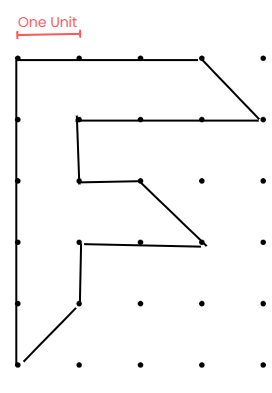
For this image of "F" in the grid, there are 16 straight and 3 diagonal lines.
- Straight lines (s) = 16
- Diagonal lines (d) = 3
- Total Perimeter = s + d = 16 + 3 = 19 units
Understanding Perimeter with Simple Examples
Example: Deep Dive
Now, imagine you’re at a playground with two paths you can run around. One path is bigger, and the other is smaller. You and your friend decide to run on different paths and see who runs the most.
- Big Path: It’s 50 meters long and 30 meters wide. To find out how far you run in one round, you calculate the perimeter of this path.
- Perimeter of Big Path = 2 × (Length + Width) = 2 × (50 m + 30 m) = 2 × 80 m = 160 m
- So, if you run around the big path once, you run 160 meters.
- Small Path: It’s 30 meters long and 20 meters wide.
- Perimeter of Small Path = 2 × (Length + Width) = 2 × (30 m + 20 m) = 2 × 50 m = 100 m
If your friend runs around the small path once, they run 100 meters.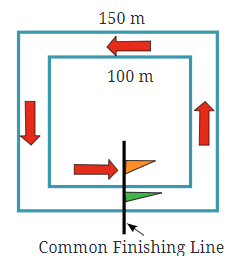
Now, if you run 3 rounds on the big path, you would run: 3 × 160 m = 480 meters
And if your friend runs 4 rounds on the small path, they would run: 4 × 100 m = 400 meters
So, even though your friend ran more rounds, you ran the longer distance (480 meters vs. 400 meters).
Example: Comparing Distances with a Simple Race
Let’s say you and your friend are going to race around two tracks, but these tracks are squares instead of rectangles:
- Big Square Track: Each side is 40 meters long.
- Small Square Track: Each side is 20 meters long.
- Perimeter of Big Square Track = 4 × Side = 4 × 40 m = 160 meters
- Perimeter of Small Square Track = 4 × Side = 4 × 20 m = 80 meters
If the race is 240 meters long, you need to figure out where to start so that you both finish at the same spot:
- On the big track, after 240 meters, you would be at 240 - 160 = 80 meters from your starting point.
- On the small track, after 240 meters, you would be at 240 - 80 = 160 meters from your starting point.
Estimate and Verify
Take a piece of paper or newspaper and cut it into different shapes, like stars, hearts, or triangles.
- First, estimate how long the edges (or the perimeter) of each shape are.
- Then, use a ruler or measuring tape to measure the actual perimeter.
See how close your estimate was!
Perimeter of Regular Polygons
A regular polygon is a closed shape where all sides and all angles are equal. For example:
- Equilateral Triangle: All three sides and all three angles are equal.
- Square: All four sides and all four angles are equal.
Perimeter of an Equilateral Triangle
The perimeter of any triangle is the sum of its three sides. For an equilateral triangle, since all three sides are the same, the perimeter is: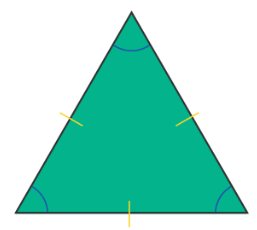

Example: Imagine you have an equilateral triangle where each side is 5 cm. The perimeter would be:
Perimeter = 3 × 5 cm = 15 cm
The similarity between a Square and an Equilateral Triangle
- Both shapes have equal sides and equal angles, making them regular polygons.
- The perimeter of each can be calculated by multiplying the number of sides by the length of one side.
Split and Rejoin Activity
You have a rectangular paper chit with dimensions 6 cm × 4 cm. 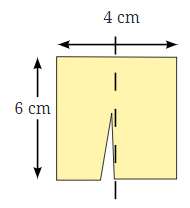
This rectangle is cut into two equal pieces and rejoined in different ways to create new shapes. Your task is to calculate the perimeter of each new shape.
Example a: 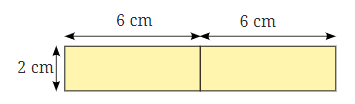
For the first arrangement, the pieces are joined side by side, creating a long rectangle. The perimeter is:
Perimeter of arrangement a:
- Top + Bottom + Left Side + Right Side
- 6 cm + 6 cm + 2 cm + 2 cm + 6 cm + 6 cm = 28 cm
Example b, c, and d:
Now, let's calculate the perimeter for each of these new shapes:
b.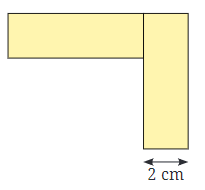
Ans:

Length of boundary = AB + BC + CD + DE + EF + FG + GA
= 6 + 2 + 6 + 2 + 4 + 6 + 2
= 28 cm
c.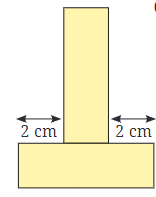
Ans
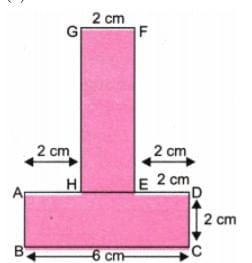
Total length of boundary = AB + BC + CD + DE +EF + FG + GH + HA
= 2 + 6 + 2 + 2 + 6 + 2 + 6 + 2
= 28 cm
d.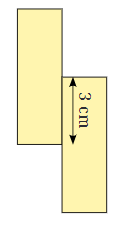
Ans:
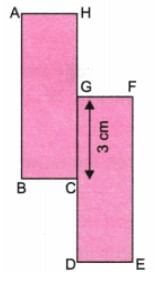
Total length of boundary = AB + BC + CD + DE + EF + FG + GH + HA
= 6 + 2 + 3 + 2 + 6 + 2 + 3 + 2
= 26 cm
Area
The amount of region enclosed by a closed figure is called its area.
Key Formulas
Area of a Square: The area of a square is calculated by multiplying the length of one side by itself.
Area of a Rectangle: The area of a rectangle is found by multiplying the length by the width.
Understanding with Examples
Example 1: Finding the Uncovered Area on a Floor
Imagine you have a rectangular room that is 5 meters long and 4 meters wide. You place a square carpet that is 3 meters on each side in the middle of the floor. How much of the floor is not covered by the carpet?
Step-by-Step Solution:
Calculate the Area of the Floor:
- Length of the floor: 5 meters
- Width of the floor: 4 meters
- Area of the floor: 5 m × 4 m = 20 square meters
Calculate the Area of the Carpet:
- Side of the carpet: 3 meters
- Area of the carpet: 3 m × 3 m = 9 square meters
Find the Uncovered Area:
- Uncovered area: Area of the floor - Area of the carpet
- Uncovered area: 20 sq m - 9 sq m = 11 sq m
So, 11 square meters of the floor are not covered by the carpet.
Real-Life Application: You can try this out at home! Measure the area of your room and then calculate how much space is taken up by your bed or a table. This will help you understand how much free space is left in your room.
Example 2: Estimating the Area of Irregular Shapes
Look at the two shapes in the image. Which one do you think has a larger area? It's not easy to tell just by looking, right? To estimate the area of these irregular shapes, we can use a method involving square or graph paper. This method is helpful when the shape isn't a simple square or rectangle. Irregular shapes on graph paper
Irregular shapes on graph paper
How to Estimate the Area Using Graph Paper:
Trace the Shape:
First, trace the shape onto a piece of transparent paper. Then, place this paper on top of a sheet of graph paper. Each small square on the graph paper represents 1 square unit.Count Full Squares:
Count all the full squares inside the shape. Each of these full squares contributes exactly 1 square unit to the area.Handle Partial Squares:
- Less than Half a Square: Ignore these. They don't contribute to the area.
- More than Half a Square: Count these as 1 square unit.
- Exactly Half a Square: Count these as 0.5 square units (or ½ square unit).
By following these steps, you can estimate the area of almost any shape.
Why Use Squares to Measure Area?
You might wonder why we use squares to measure area instead of other shapes like circles or triangles. Let’s explore this:
- Squares Fit Perfectly: When you cover an area with squares, there are no gaps or overlaps. This makes the measurement accurate.
- Circles or Other Shapes: If you tried to measure the area using circles, you’d notice that circles don’t fit together perfectly without leaving gaps. This makes it hard to measure the area accurately.
Area of a Triangle
Understanding with Examples
Example 1: In the image, you see a rectangle with a diagonal line . This diagonal splits the rectangle into two triangles: the blue triangle and the yellow triangle .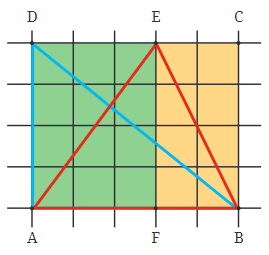
Solution:
- Imagine a rectangle ABCD on graph paper. The corners of the rectangle are labelled A, B, C, and D.
- The rectangle is divided into two triangles by drawing a diagonal line from point B to point D, creating triangles BAD and BCD.
Calculating the Area of the Rectangle ABCD
- To find the area of the rectangle, count the number of square units within it. Each square on the graph paper represents 1 square unit.
- For example, if the rectangle is 5 squares long (from A to B) and 4 squares wide (from A to D), the area is calculated as follows:
- Area of ABCD = Length × Width
- Area of ABCD = 5 squares × 4 squares = 20 square units.
Understanding the Area of Triangle BAD
- Triangle BAD is formed by cutting the rectangle along the diagonal BD.
- Since the diagonal divides the rectangle into two equal halves, the area of triangle BAD is half of the area of the rectangle ABCD.
- Formula: Area of triangle BAD = ½ × Area of rectangle ABCD
- Using our earlier example, if the area of ABCD is 20 square units:
- Area of triangle BAD = ½ × 20 square units = 10 square units.
Exploring Triangle ABE
- Triangle ABE is formed by another diagonal within the rectangle, dividing it into smaller sections.
- This triangle can be split further into two smaller triangles: AEF and BEF.
- The area of triangle ABE is the sum of the areas of triangles AEF and BEF.
- Each of these smaller triangles (AEF and BEF) is half of the area of the smaller rectangles they fit into within ABCD.
Breaking Down Triangle ABE
- The area of triangle AEF is half the area of the smaller rectangle AFED.
- Similarly, the area of triangle BEF is half the area of the smaller rectangle BFEC.
- So, the area of triangle ABE is half the sum of the areas of rectangles AFED and BFEC.
- This also means that triangle ABE’s area is half of the area of the larger rectangle ABCD.
- By cutting a rectangle along its diagonal, you create two triangles, each with an area that is exactly half of the rectangle’s area.
- Whether you’re dealing with triangle BAD or ABE, the relationship remains the same: both triangles cover half the area of the rectangle ABCD
Example 2: Making it 'More' or 'Less'
In the images you provided, there are two figures made up of 9 unit squares. Each square has an area of 1 square unit, so both figures have an area of 9 square units.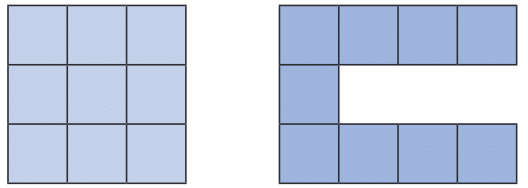
However, these two figures have different perimeters. The first figure has a perimeter of 12 units, and the second figure has a perimeter of 20 units.
Solution:
Exploring Perimeter with 9 Unit Squares:
- Smallest Perimeter Possible: The smallest perimeter happens when you arrange the squares into the most compact shape. This usually happens when you make a 3x3 square. The perimeter in this case would be 12 units.
- Largest Perimeter Possible: The largest perimeter happens when the squares are arranged in a single line. The perimeter in this case would be 20 units.
- Making a Figure with a Perimeter of 18 Units: You can experiment by arranging the squares into different shapes. One possible shape with a perimeter of 18 units is an "L" shape with 2 squares on one side and 3 squares on the other side.
Adding a New Square to the Shape: If you add a new square to the shape with a perimeter of 24 units, the change in perimeter depends on where you place the new square.
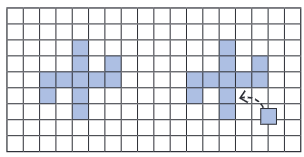
- If the perimeter increases: This happens when the new square is placed in such a way that it adds more sides to the outer edge of the figure.
- If the perimeter decreases: This happens if the new square fills in a gap, reducing the number of exposed sides.
- If the perimeter stays the same: This occurs when the new square aligns perfectly with an existing side, not adding any new sides to the outer edge.
Key points
- Perimeter is the total distance around a closed shape.
- The perimeter of a polygon is the sum of the lengths of all its sides.
- The perimeter of a rectangle is calculated as 2 × (Length + Width).
- The perimeter of a square is calculated as 4 × Length of one side.
- The perimeter of a triangle is the sum of the lengths of its three sides.
- For shapes on a grid, the perimeter includes both straight and diagonal lines.
- Area is the amount of space inside a closed shape, measured in square units.
- The area of a square is calculated as Side × Side.
- The area of a rectangle is calculated as Length × Width.
- Estimating the area of irregular shapes can be done using graph paper by counting full and partial squares.
- Cutting a rectangle diagonally creates two triangles, each with half the area of the rectangle.
- To find the area and perimeter of a house plan, calculate each room’s area and add them up for the total area; sum the outer sides for the total perimeter.
- Comparing house plans involves calculating and comparing their total area and perimeter.
FAQs on Perimeter and Area Chapter Notes - Chapter Notes For Class 6
| 1. What is the formula for calculating the perimeter of a rectangle? |  |
| 2. How do you find the area of a triangle? |  |
| 3. What is the difference between perimeter and area? |  |
| 4. Can you explain how to calculate the area of a circle? |  |
| 5. What units should be used when calculating perimeter and area? |  |





















