Perimeter and Area NCERT Solutions | Mathematics (Maths) Class 6 PDF Download
| Table of contents |

|
| Page 132 |

|
| Page 133 |

|
| Page 134 |

|
| Page 135 |

|
| Page 136 |

|
| Page 138 |

|
| Page 140 |

|
| Page 141 |

|
| Page 142 |

|
| Page 143 |

|
| Page 144 |

|
| Page 145 |

|
| Page 146 |

|
| Page 149 |

|
Page 132
Q1: Find the missing terms:
(a) Perimeter of a rectangle = 14 cm; breadth = 2 cm; length = ?
Ans: We know that perimeter of a rectangle = 2(l + b)
Here, the perimeter of the rectangle = 14 cm and breadth b = 2 cm, l =?
Thus 14 = 2(l + 2)
⇒ 14 = 2l + 4
⇒ 2l = 14 – 4 = 10
⇒ l = 10/2 = 5 cm
(b) Perimeter of a square = 20 cm; side of length = ?
Ans: We know that the perimeter of the square = 4 × a
where a = side of the square
∴ 20 = 4 × a
⇒ a = 5 cm
(c) Perimeter of a rectangle = 12 m; length = 3 m; breadth = ?
Ans: Perimeter of rectangle = 2(l + b)
⇒ 12 = 2(3 + b)
⇒ 12 = 6 + 2b
⇒ 12 – 6 = 2b
⇒ 2b = 6 m
⇒ b = 3 m
Q2: A rectangle having side lengths 5 cm and 3 cm is made using a piece of wire. If the wire is straightened and then bent to form a square, what will be the length of a side of the square?
Ans: Here perimeter of rectangle = 2(5 + 3)
= 2 × 8
= 16 cm
Now the wire is straightened and then bent to form a square.
∴ Perimeter of square = 16 cm
⇒ 4a = 16 cm
⇒ a = 4 cm, the required length of the side of the square.
Q3: Find the length of the third side of a triangle having a perimeter of 55 cm and having two sides of length 20 cm and 14 cm, respectively.
Ans: 
First side of the triangle = 20 cm
Second side of the triangle = 14 cm
Let third side Of the triangle be 'x'
Perimeter of the triangle = 55cm
∴ 20 + 14 + x = 55cm
34 + x = 55
x = 55 - 34
x = 21 cm.
Therefore, length of the third side of the triangle is 21 cm.
Q4: What would be the cost of fencing a rectangular park whose length is 150 m and breadth is 120 m, if the fence costs ₹ 40 per metre?
Ans: The length of the fence is the perimeter of the rectangular park.
Given that the length of the rectangular park = 150 m and breadth = 120 m
∴ Perimeter = 2(l + b)
= 2(150 + 120)
= 2(270)
= 540 m
Now cost of fencing per meter = ₹ 40
Cost of fencing the rectangular park = ₹ 40 × 540 = ₹ 21600
Q5: A piece of string is 36 cm long. What will be the length of each side if it is used to form:
(a) A square
Ans: Given, a piece of string is 36 cm long
∴ length of each side of the square = a
perimeter = 36
⇒ 4a = 36
⇒ a = 9 cm
(b) A triangle with all sides of equal length
Ans: Length of each side of the triangle = 3a (Given)
perimeter = 36
⇒ 3a = 36
⇒ a = 12 cm
(c) A hexagon (a six-sided closed figure) with sides of equal length?
Ans: Length of each side of hexagon = a
perimeter = 36
⇒ 36 = 6a
⇒ a = 6 cm
Q6: A farmer has a rectangular field having a length of 230 m and a breadth of 160 m. He wants to fence it with 3 rounds of rope as shown. What is the total length of rope needed? Ans: Perimeter of the rectangular field = 2(l + b)
Ans: Perimeter of the rectangular field = 2(l + b)
Here l = 230 m, b = 160 m
∴ P = 2(230 + 160)
= 2 (390)
= 780 m
Distance covered by a farmer in one round = 780 m
∴ Total length of rope needed = 3 × 780 = 2340 m
Page 133
Matha Pachchi!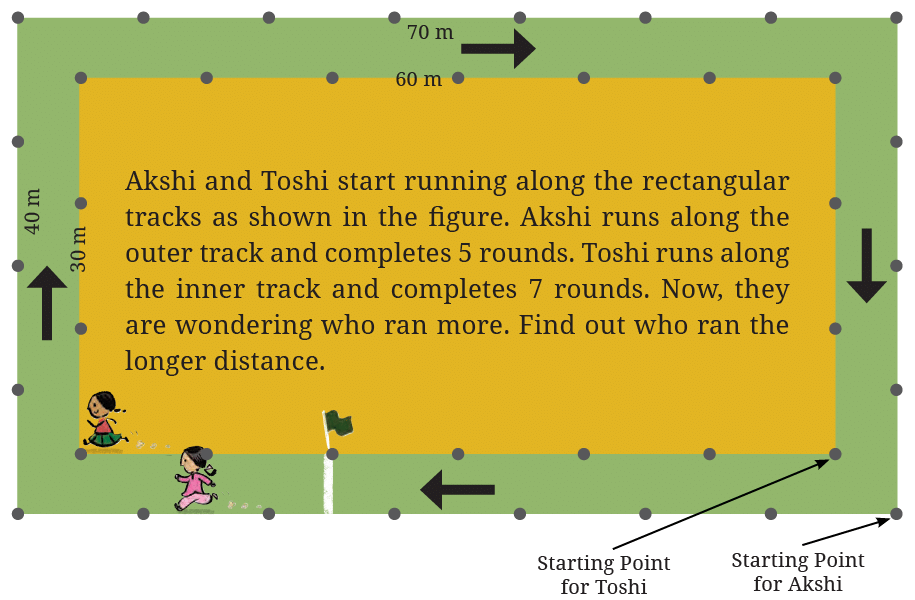 Each track is a rectangle. Akshi’s track has length 70 m and breadth 40 m. Running one complete round on this track would cover 220 m, i.e., 2 × (70 + 40) m = 220 m. This is the distance covered by Akshi in one round.
Each track is a rectangle. Akshi’s track has length 70 m and breadth 40 m. Running one complete round on this track would cover 220 m, i.e., 2 × (70 + 40) m = 220 m. This is the distance covered by Akshi in one round.
Figure it Out
Q1: Find out the total distance Akshi has covered in 5 rounds.
Ans: Distance covered by Akshi in 5 rounds = 5 × perimeter of PQRS
= 5 × 220
= 1100 m
Q2: Find out the total distance Toshi has covered in 7 rounds. Who ran a longer distance?
Ans: Distance covered by Toshi in 7 rounds = 7 × 180 = 1260 m
∴ 1260 m > 1100 m
Hence Toshi ran the longer distance.
Q3: Think and mark the positions as directed:
(a) Mark ‘A’ at the point where Akshi will be after she ran 250 m.
Ans: Here,
1. One complete round = 220 meters.
2. Distance Akshi has run = 250 meters.
3. Extra distance beyond one round = 250 – 220 = 30 meters.
Since Akshi has already completed one full round, she will be 30 meters into her second round. So, after running 30 meters more, she will be on the length side of the track, 30 meters from the starting point. Therefore, mark ‘A’ at the point 30 meters along the length of the track from the starting point.
(b) Mark ‘B’ at the point where Akshi will be after she ran 500 m.
Ans: Distance per round = 220 meters
Total distance Akshi runs = 500 meters.
First, we will find out how many complete rounds she runs:
Number of complete rounds = 500/220 = 2.27 (approx.)
This means Akshi completes 2 full rounds and then runs an additional distance = 500 – (2 × 220) = 60 m
Therefore, Akshi will be 60 meters along the length of the track from the starting point, we can mark point ‘B’ at this position on the track.
(c) Now, Akshi ran 1000 m. How many full rounds has she finished running around her track? Mark her position as ‘C’.
Ans: Now, Akshi ran 1000 meters. To find out how many full rounds she completed, we divide the total distance she ran by the perimeter of the track:
Number of full rounds = 1000/220 = 4.545 rounds.
Akshi has completed 4 full rounds and is partway through her 5th round.
To find her position on the track, we calculate the remaining distance after 4 full rounds:
Remaining distance = 1000 m – (4 × 220 m)
= 1000 m – 880 m
= 120 m
Since she has run an additional 120 meters after completing 4 full rounds, her position will be 120 meters from the starting point. If we mark her starting point as ‘P’, her position after running 1000 meters can be marked as ‘C’, which is 120 meters from ‘A’ along the track.
(d) Mark ‘X’ at the point where Toshi will be after she ran 250 m.
Ans: Here,
1. Perimeter of the track = 180 meters
2. Distance Toshi runs = 250 meters
Since 250 meters is more than one complete round (180 meters), Toshi will have completed one full round and will have 70 meters left to run (250 – 180 = 70 meters). So, Toshi will be 70 meters along the length of the track from the starting point. You can mark ‘X’ at this point on the track.
(e) Mark ‘Y’ at the point where Toshi will be after she ran 500 m.
Ans: Given, that Toshi has run an additional 140 meters after completing 2 rounds, her position will be 140 meters from the starting point. If we mark her starting point as ‘A’, her position after running 500 meters can be marked as ‘Y’.
(f) Now, Toshi ran 1000 m. How many full rounds has she finished running around her track? Mark her position as ‘Z’.
Ans: Here, we need to find out how many full rounds Toshi has completed by dividing the total distance she ran by the perimeter of the track:
Number of full rounds = 1000/180 = 5.56
Toshi has finished 5 full rounds.
Remaining distance = 1000 meters – (5 × 180 meters)
= 1000 meters – 900 meters
= 100 meters
Starting from the initial point, Toshi would be 100 meters into her 6th round. Since the track is 60 meters long and 30 meters wide, she would be somewhere along the length of the track.
Let’s mark this position as ‘Z’.
Page 134
Q: Deep Dive:
In races, usually, there is a common finish line for all the runners. Here are two square running tracks with an inner track of 100 m on each side and an outer track of 150 m on each side. The common finishing line for both runners is shown by the flags in the figure which are in the center of one of the sides of the tracks. If the total race is 350 m, then we have to find out where the starting positions of the two runners should be on these two tracks so that they both have a common finishing line after they run for 350 m. Mark the starting points of the runner on the inner track as ‘A ’ and the runner on the outer track as ‘B’. Ans: Inner Track (100 m per side)
Ans: Inner Track (100 m per side)
Perimeter Calculation: The perimeter of the inner track is (4 times 100 = 400) meters.
Distance to Run: The runner on the inner track needs to run 350 meters.
Starting Position (A): Since the perimeter is 400 meters, the runner will start 50 meters before the common finish line (400 – 350 = 50 meters).
Outer Track (150 m per side)
Perimeter Calculation: The perimeter of the outer track is (4 times 150 = 600) meters.
Distance to Run: The runner on the outer track also needs to run 350 meters.
Starting Position (B): Since the perimeter is 600 meters, the runner will start 250 meters before the common finish line (600 – 350 = 250 meters).
Q: Estimate and Verify
Take a rough sheet of paper or a sheet of newspaper. Make a few random shapes by cutting the paper in different ways. Estimate the total length of the boundaries of each shape then use a scale or measuring tape to measure and verify the perimeter for each shape.
Ans:  For estimating the total length of the boundaries of each shape, we can estimate the perimeter visually. Since the shapes are irregular and torn in different ways, visually estimate the boundary lengths by counting how many straight segments or curves each shape has. Break the boundary into smaller, more manageable parts.
For estimating the total length of the boundaries of each shape, we can estimate the perimeter visually. Since the shapes are irregular and torn in different ways, visually estimate the boundary lengths by counting how many straight segments or curves each shape has. Break the boundary into smaller, more manageable parts.
Q: Akshi says that the perimeter of this triangle shape is 9 units. Toshi says it can’t be 9 units and the perimeter will be more than 9 units. What do you think?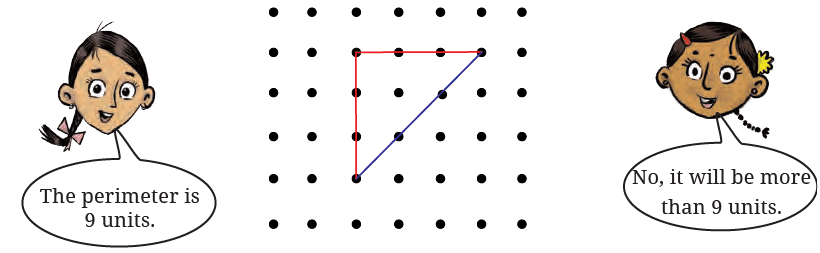
Ans: Akshi's statement that the perimeter is 9 units is not correct. Toshi is right-since the diagonal lines are longer than the straight lines, the perimeter is more than 9 units. In fact, the correct perimeter is more than 10 units.
Page 135
This figure has lines of two different unit lengths. Measure the lengths of a red line and a blue line; are they same? We will call the red lines-straight lines and the blue lines-diagonal lines. So, the perimeter of this triangle is 6 straight units + 3 diagonal units. We can write this in a short form as: 6s + 3d units.
Q: Write the perimeters of the figures below in terms of straight and diagonal units.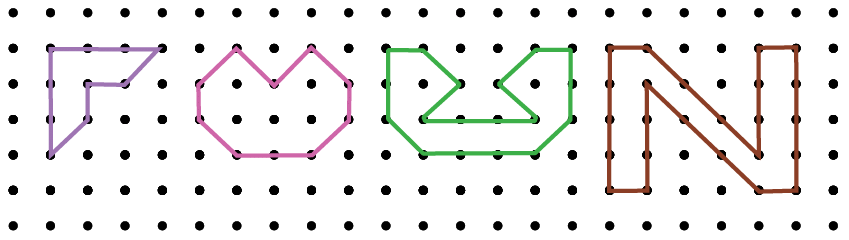 Ans: Figure 1: 8s + 2d units
Ans: Figure 1: 8s + 2d units
Figure 2: 4s + 6d units
Figure 3: 12s + 6d units
Figure 4: 18s + 6d units
Page 136
Q: Split and Rejoin
A rectangular paper chit of dimension 6 cm × 4 cm is cut as shown into two equal pieces. These two pieces are joined in different ways. a.
a.
For example, the arrangement a. has a perimeter of 28 cm.
Find out the length of the boundary (i.e., the perimeter) of each of the other arrangements below.
Ans:
(b)
∴ Length of boundary = AB + BC + CD + DE + EF + FG + GA
= 6 + 2 + 6 + 2 + 4 + 6 + 2
= 28 cm
(c)
 Total length of boundary = AB + BC + CD + DE +EF + FG + GH + HA
Total length of boundary = AB + BC + CD + DE +EF + FG + GH + HA
= 2 + 6 + 2 + 2 + 6 + 2 + 6 + 2
= 28 cm
(d) 
Total length of boundary = AB + BC + CD + DE + EF + FG + GH + HA
= 6 + 2 + 3 + 2 + 6 + 2 + 3 + 2
= 26 cm
Q: Arrange the two pieces to form a figure with a perimeter of 22 cm.
Ans: Arranging the two pieces in such a way that they form a new shape with the desired perimeter:
Page 138
Q1: The area of a rectangular garden 25 m long is 300 sq m. What is the width of the garden?
Ans: Given, area of rectangular garden = 300 sq.m
and length = 25 m
area of rectangular field = l × b
⇒ 300 = 25 × b
⇒ b = 12 m
Q2: What is the cost of tiling a rectangular plot of land 500 m long and 200 m wide at the rate of ₹8 per hundred sq m?
Ans: Here, length = 500 m and breadth = 200 m
Hence the area of the rectangular plot = length × breadth
= 500 × 200
= 1,00,000 m2
Now cost of tilling a rectangular plot = 8/100
Hence the cost of tilling 1,00,000 sq. m of rectangular plot = 8/100 × 100000 = ₹ 8,000
Q3: A rectangular coconut grove is 100 m long and 50 m wide. If each coconut tree requires 25 sq m, what is the maximum number of trees that can be planted in this grove?
Ans: Area of rectangular coconut grove = 100 × 50 = 5000 sq. m
Given each coconut tree requires 25 sq. m
then the maximum no. of trees that can be planted in this grove = 5000/25 = 200
Q4: By splitting the following figures into rectangles, find their areas (all measures are given in metres).
(a)
Ans: By splitting the following figures into rectangles, we find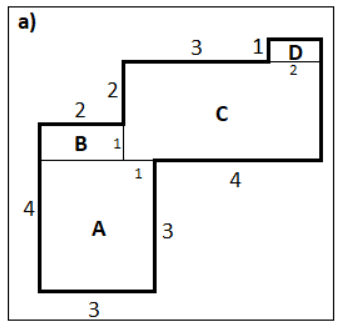
Area of the rectangle A = 3 × 3 m = 9 m
Area of the rectangle B = 2 × (4 - 3) m = 2 × 1 m = 2 m
Area of the rectangle C = (4 + 1) × (2 + 1) m = 5 × 3 m = 15 m
Area of the rectangle D = {(4 + 1) – 3} × 1 = 2 × 1 m = 2 m
(b) 
Ans: By splitting the following figures into rectangles, we find Area of the rectangle (I) = 5 × (3 - 2) m = 5 × 1 m = 5 m
Area of the rectangle (I) = 5 × (3 - 2) m = 5 × 1 m = 5 m
Area of the rectangle (II) = (2 × 1) m = 2 m
Area of the rectangle (III) = (2 × 1) m = 2 m
Page 139
Q1: Explore and figure out how many pieces have the same area.
Ans: Shape C and Shape E are the two pieces with the same area.
Q2: How many times bigger is Shape D as compared to Shape C? What is the relationship between Shapes C, D, and E?
Ans: Shape D is twice bigger in size than Shape C.
The area of Shape D is equal to sum of areas of Shape C and Shape E together i.e Shape C + Shape E = Shape D.
Q3: Which shape has more area: Shape D or F? Give reasons for your answer.
Ans: Both Shape D and Shape F have equal area.
It's because Shape C and Shape E together fit perfectly into both Shape D and Shape F.
Q4: Which shape has more area: Shape F or G? Give reasons for your answer.
Ans: Both Shape F and Shape G have equal area.
It's because Shape C and Shape E together fit perfectly into both Shape F and Shape G.
Q5: What is the area of Shape A as compared to Shape G? Is it twice as big? Four times as big?
[Hint: In the tangram pieces, by placing the shapes over each other, we can find out that Shapes A and B have the same area, and Shapes C and E have the same area. You would have also figured out that Shape D can be exactly covered using Shapes C and E, which means Shape D has twice the area of Shape C or Shape E, etc.]
Ans: The area of Shape A is twice as big as Shape G.
Q6: Can you now figure out the area of the big square formed with all seven pieces in terms of the area of Shape C?
Ans: The area of big square is 16 times the area of Shape C.
Q7: Arrange these 7 pieces to form a rectangle. What will be the area of this rectangle in terms of the area of Shape C now? Give reasons for your answer.
Ans: The area Of the rectangle formed by combining all 7 pieces will be 16 times the area of Shape c.
This is because the total area Of all the pieces will remain the same, regardless Of how they are aligned.
Q8: Are the perimeters of the square and the rectangle formed from these 7 pieces different or the same? Give an explanation for your answer.
Ans: The perimeter of the square and the rectangle formed from these 7 pieces will be different.
This is because the distance around outside of the shape is different.
Page 140
Q: Look at the figures below and guess which one of them has a larger area.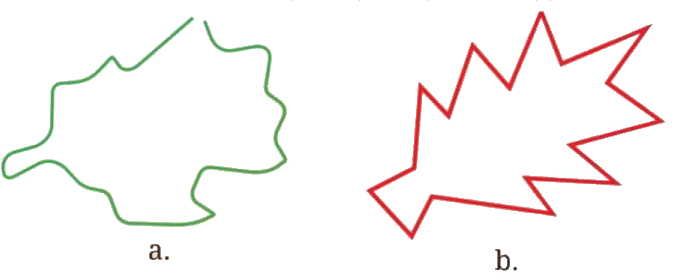 Ans: Shape (b) has larger area.
Ans: Shape (b) has larger area.
Q: Find the area of the following figures. Ans: Area of figure 1 = 4 square units.
Ans: Area of figure 1 = 4 square units.
Area of figure 2 = 9 square units.
Area of figure 3 = 10 square units.
Area of figure 4 = 11 square units.
Page 141
Try using different shapes (triangle and rectangle) to fill the given space (without overlaps and gaps) and find out the merits associated with using a square shape to find the area rather than another shape. List out the points that make a square the best shape to use to measure area.
1. Find the area (in square metres) of the floor outside of the corridor.
2. Find the area (in square metres) occupied by your school playground.
Ans:
1. The area (in square metres) of the floor outside of the corridor = 1200
2. The area (in square metres) occupied by your school playground = 9000
Let’s Explore!
On a squared grid paper (1 square = 1 square unit), make as many rectangles as you can whose lengths and widths are a whole number of units such that the area of the rectangle is 24 square units.
a. Which rectangle has the greatest perimeter?
b. Which rectangle has the least perimeter?
c. If you take a rectangle of area 32 sq cm, what will your answers be? Given any area, is it possible to predict the shape of the rectangle with the greatest perimeter as well as the least perimeter? Give examples and reasons for your answer.
Ans: Rectangles with area 24 square units: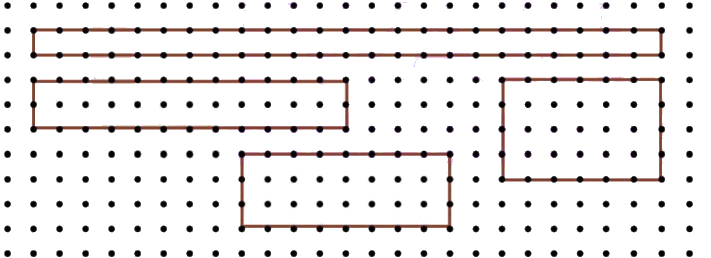 a. First rectangle has the greatest perimeter 50 units.
a. First rectangle has the greatest perimeter 50 units.
b. Last rectangle has the least perimeter 20 units.
c. If you take a rectangle of area 32 sq cm: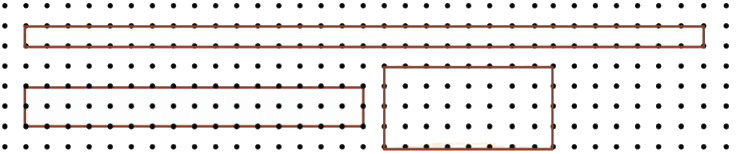 The greatest perimeter 66 units.
The greatest perimeter 66 units.
The least perimeter 24 units.
 |
Download the notes
NCERT Solutions: Perimeter and Area
|
Download as PDF |
Page 142
Q: Draw a rectangle on a piece of paper and draw one of its diagonals. Cut the rectangle along that diagonal and get two triangles.
Check! whether the two triangles overlap each other exactly. Do they have the same area?
Try this with more rectangles having different dimensions. You can check this for a square as well.
Ans: Yes, the two triangles overlap each other exactly. They have the same area as shown in figure.
Q: Now, see the figures below. Is the area of the blue rectangle more or less than the area of the yellow triangle? Or is it the same? Why?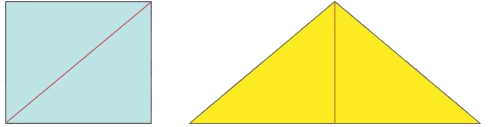 Can you see some relationship between the blue rectangle and the yellow triangle and their areas? Write the relationship here.
Can you see some relationship between the blue rectangle and the yellow triangle and their areas? Write the relationship here.
Ans: The area of blue rectangle and yellow triangle are equal.
Area of Rectangle = 2 x Area of triangle
Page 143
Q: Use your understanding from previous grades to calculate the area of any closed figure using grid paper and 1. Find the area of the blue triangle BAD.
1. Find the area of the blue triangle BAD.
2. Find the area of the red triangle ABE.
Ans: 1. Area of blue triangle BAD
∴ Total area of BAD = 6 + 1 + 3 = 10 sq. units
2. Area of red triangle ABE
∴ Total area of ABE = 5 + 1 + 4 = 10 sq. units
Area of rectangle ABCD = Number of fully tilled squares
= 20 × 1
= 20 sq. units
Page 144
Q1: Find the areas of the figures below by dividing them into rectangles and triangles.
Ans:  (a) Area of the figure = Area of triangle A + Area of triangle B + Area of rect. C
(a) Area of the figure = Area of triangle A + Area of triangle B + Area of rect. C
= 3 sq. units + 3 sq. units + 20 sq. units
= 26 sq. units.
(b) Area of the figure = Area of triangle P + Area of triangle Q + Area of rect. R
= 6 sq. units +4 sq. units + 20 sq. units
= 30 sq. units.
(c) Area = Area of triangle G + Area of triangle E + Area of triangle F + Area of rect. D
= 3 sq. units + 18 sq. units + 3 sq. units + 24 sq. units
= 48 sq. units.
(d) Area of the figure = Area of triangle W + Area of triangle U + Area of rect. V
= 1 sq. units + 3 sq. units + 12 sq. units
= 16 sq. units.
(e) Area of the figure = Area of triangle T + Area of triangle P
= 4 sq. units + 7 sq. units
= 11 sq. units.
Page 145
Using 9 unit squares, solve the following. Q1: What is the smallest perimeter possible?
Q1: What is the smallest perimeter possible?
Ans: The smallest perimeter is achieved by forming a 3 × 3 square: Perimeter = 3 + 3 + 3 + 3 = 12 units.
Perimeter = 3 + 3 + 3 + 3 = 12 units.
Q2: What is the largest perimeter possible?
Ans: The largest perimeter is achieved by arranging the squares in a straight line:
Perimeter = 1 + 9 + 1 + 9 = 20 units.  Q3: Make a figure with a perimeter of 18 units.
Q3: Make a figure with a perimeter of 18 units.
Ans: One possible figure is an L-shaped arrangement: Arrange 6 squares in a vertical line and 3 squares in a horizontal line at the bottom.Perimeter = 6 + 3 + 1 + 1 + 1 + 1 + 1 + 1 + 3 = 18 units.
Arrange 6 squares in a vertical line and 3 squares in a horizontal line at the bottom.Perimeter = 6 + 3 + 1 + 1 + 1 + 1 + 1 + 1 + 3 = 18 units.
Q4: Can you make other shaped figures for each of the above three perimeters, or is there only one shape with that perimeter? What is your reasoning?
Ans: Smallest Perimeter (12 units): Only the 3 × 3 square achieves this.
Largest Perimeter (20 units): Only the straight line achieves this or any pattern made by folding two straight lines. Perimeter of 18 units: Multiple shapes can achieve this. For example, a T-shaped figure or other L-shaped configurations.
Perimeter of 18 units: Multiple shapes can achieve this. For example, a T-shaped figure or other L-shaped configurations. The reasoning is based on the arrangement of the unit squares and the number of exposed edges. The more compact the shape, the smaller the perimeter; the more elongated, the larger the perimeter. For intermediate perimeters like 18 units, various configurations can be created by adjusting the arrangement of the squares.
The reasoning is based on the arrangement of the unit squares and the number of exposed edges. The more compact the shape, the smaller the perimeter; the more elongated, the larger the perimeter. For intermediate perimeters like 18 units, various configurations can be created by adjusting the arrangement of the squares.
Page 146
Q1: Below is the house plan of Charan. It is in a rectangular plot. Look at the plan. What do you notice? 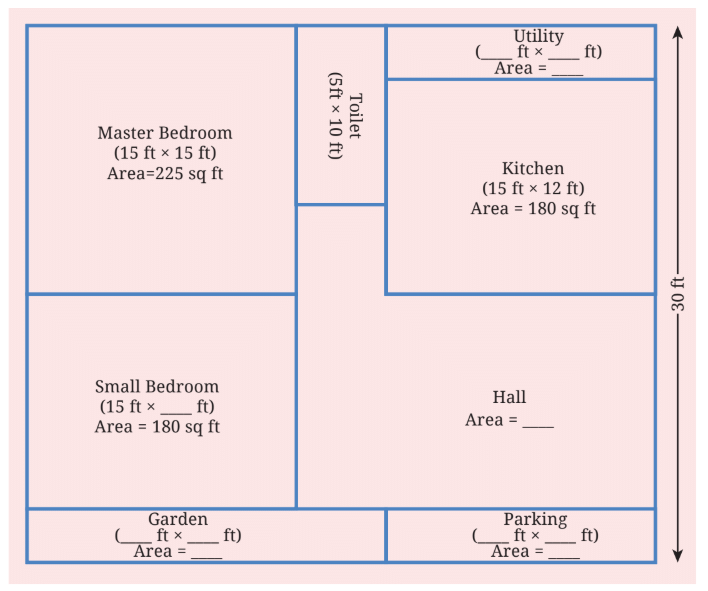
Some of the measurements are given.
(a) Find the missing measurements.
(b) Find out the area of his house.
Ans:
(a) Utility = 15 ft x 3 ft = 45 sq ft
Small Bedroom = 15 ft x 12 ft = 180 sq ft
Garden = 3 ft x 20 ft = 60 sq ft
Parking = 3 ft x 15 ft = 45 sq ft
Hall = Total Area of the House - Area of (Utility + Small Bedroom + Garden + Parking + Master Bedroom + Toilet + Kitchen)
Total area of the house is 35 ft x 30 ft which is 1050 sq ft.
Area of hall = 1050 - (45 + 180 + 60 + 45 + 225 + 50 + 180) = 1050 - 785 = 265 sq ft.
(b) Area of his house = 35 ft x 30 ft = 1050 sq ft.
Page 149
Q1: Give the dimensions of a rectangle whose area is the sum of the areas of these two rectangles having measurements: 5 m × 10 m and 2 m × 7 m.
Ans: The sum of the areas of these two rectangles = (5 × 10 + 2 × 7) sq m = 64 sq m
Now, the rectangle has the area of 64 sq m
So, the dimensions of rectangle = 16 m × 4 m
(64 = 2 × 2 × 2 × 2 × 2 × 2)
Q2: The area of a rectangular garden that is 50 m long is 1000 sq m. Find the width of the garden.
Ans: Length of a rectangular garden = 50 m
Area of the rectangular garden = 1000 sq m
Now,
∴ Area of the rectangular garden = length × width
∴ 1000 = 50 × width
∴ Width = 1000/50 = 20
So, the width of the rectangular garden = 20 m
Q3: The floor of a room is 5 m long and 4 m wide. A square carpet whose sides are 3 m in length is laid on the floor. Find the area that is not carpeted.
Ans: Length of a room = 5 m
Width of the room = 4 m
So, area of the room = 5 × 4 sq m = 20 sq m
Now, length of sides of a square carpet = 3 m
Area of the carpet = 3 × 3 sq m = 9 sq m
The area that is not carpeted is = (20-9) sq m = 11 sq m
Q4: Four flower beds having sides 2 m long and 1 m wide are dug at the four corners of a garden that is 15 m long and 12 m wide. How much area is now available for laying down a lawn?
Ans: Length of garden = 15 m
Width of garden = 12 m
So, the area of the garden = 15 × 12 sq m = 180 sq m
Now, length of flower bed = 2 m
Width of flower bed = 1 m
Area of the flower bed = 2 × 1 sq m = 2 sq m
Since, the area of four flower beds = 2 × 4 sq m = 8 sq m
Now the area is available for laying down a lawn = (180-8) sq m = 172 sq m
Q5: Shape A has an area of 18 square units and Shape B has an area of 20 square units. Shape A has a longer perimeter than Shape B. Draw two such shapes satisfying the given conditions.
Ans: 
Q6: On a page in your book, draw a rectangular border that is 1 cm from the top and bottom and 1.5 cm from the left and right sides. What is the perimeter of the border?
Ans: So, the perimeter of the rectangle border = 2 × (length × width)
∴ Perimeter = 2 × (1 + 1.5) cm = 2 × 2.5 cm = 5 cm
Q7: Draw a rectangle of size 12 units × 8 units. Draw another rectangle inside it, without touching the outer rectangle that occupies exactly half the area.
Ans: Area of rectangle = 12 × 8 sq units = 96sq units
The area of new rectangle is half of this rectangle, so the area of new rectangle = ½ × 96 sq m = 48 sq m
(48 = 2 × 2 × 2 × 2 × 3)
Dimensions of new rectangle = 8 units × 6 units
Q8: A square piece of paper is folded in half. The square is then cut into two rectangles along the fold. Regardless of the size of the square, one of the following statements is always true. Which statement is true here?
a. The area of each rectangle is larger than the area of the square.
b. The perimeter of the square is greater than the perimeters of both the rectangles added together.
c. The perimeters of both the rectangles added together is always 1+(1/2) times the perimeter of the square.
d. The area of the square is always three times as large as the areas of both rectangles added together.
Ans: a. False because area of each rectangle is exactly half of the area of the square.
a. False because area of each rectangle is exactly half of the area of the square.
b. False because the perimeter of the two resulting rectangles combined is greater than perimeter of the square.
c. False because it can vary for different size of squares.
d. False because the area of the square is equal to sum of area of both the rectangles combined.
|
92 videos|348 docs|54 tests
|
FAQs on Perimeter and Area NCERT Solutions - Mathematics (Maths) Class 6
| 1. What is the formula for calculating the perimeter of a rectangle? |  |
| 2. How do you find the area of a triangle? |  |
| 3. What is the difference between perimeter and area? |  |
| 4. How can I find the area of a circle? |  |
| 5. What units are used for measuring perimeter and area? |  |




























