Error Analysis | Electrical and Electronic Measurements - Electrical Engineering (EE) PDF Download
True Value
The true value of a quantity is theoretically defined as the average of an infinite number of measurements, where the average deviation approaches zero. However, it cannot be exactly determined by experiments.Measured Value
A measured value is an approximation of the true value. It is obtained by averaging several readings taken during an experiment, with appropriate adjustments made for physical conditions.Static Error
Static error is the difference between the measured value and the true value of a quantity. Mathematically, it is expressed as:dA = Am− At
Where:
- dA is the static error.
- Am is the measured value.
- At is the true value.
The absolute value of the error cannot be determined exactly because the true value is unknown.
Limiting Errors or Guarantee Errors
Limiting errors, also known as guarantee errors, are the maximum error limits that a manufacturer specifies for an instrument. For example, if a manufacturer produces an ammeter, they must declare that the error in the ammeter will not exceed a specified limit. This declared limit is the limiting error.Relative Error or Fractional Error
Relative error is the ratio of the error to the specified magnitude of the quantity being measured. It is mathematically expressed as: Where:
Where:- dA is the error.
- A is the magnitude of the quantity.
Resultant Limiting Error
(a) Sum of Two Quantities: Consider two measured quantities a1 and a2, where their sum is represented as A = a1 + a2. The relative incremental value of this function can be calculated, and the resultant limiting error is the sum of the products of individual relative limiting errors multiplied by the ratio of each term to the function. The same procedure applies to more than two quantities. For the difference between two quantities, the addition sign is simply replaced by subtraction.(b) Product of Two Quantities:
Consider two quantities a1 and a2. The product is expressed as A = a1 × a2. By taking the logarithm of both sides and differentiating with respect to A, the resultant limiting error can be calculated. The resultant error is the sum of the relative errors in the measurement of terms. For power factors, the relative error would be n times in this case.
Types of Errors
Errors in measurements can be broadly classified into three categories based on their sources:Gross Errors
Gross errors result from human mistakes during reading, recording, or calculating. Examples include reading a value incorrectly, such as mistaking 21 for 31. Gross errors can be minimized by:- Taking proper care in reading and recording data.
- Increasing the number of experimenters and averaging their readings to reduce errors.
Systematic Errors
Systematic errors are consistent and repeatable errors that arise due to the following:- Instrumental Errors: These occur due to faulty construction, calibration, friction, or hysteresis in measuring instruments. They can be minimized by applying correction factors or re-calibrating the instruments.
- Environmental Errors: These arise from external factors such as temperature, pressure, humidity, or magnetic fields. They can be minimized by maintaining constant environmental conditions and shielding the instrument from external fields.
- Observational Errors: These occur due to incorrect observations, often caused by parallax. Using highly accurate meters with mirrored scales can minimize parallax errors.
Random Errors
Even after accounting for systematic errors, some errors remain, which are known as random errors. These errors may arise from unknown or unpredictable factors, and although they cannot be fully eliminated, their effects can be reduced through careful experimentation.
Estimating Experimental Uncertainty for a Single Measurement
When making any measurement, some degree of uncertainty is inevitable, regardless of the precision of the measuring tool. Estimating and reporting this uncertainty is crucial for providing a complete and accurate description of the measurement.
Factors Influencing Uncertainty
Precision and Accuracy of the Instrument: The inherent precision and accuracy of the measuring instrument directly influence the uncertainty of the measurement. Precision refers to the smallest unit that the instrument can reliably measure, while accuracy refers to how close the measurement is to the true value.
Experimental Conditions: Various factors, such as environmental conditions, the skill of the experimenter, and the specific characteristics of the object being measured, can affect the uncertainty. For example:
- Parallax Error: This occurs when the reading is taken from an angle rather than directly in line with the measurement, which can introduce uncertainty.
- Ambiguity in Definition: In some cases, the object’s properties may not be well-defined (e.g., measuring the diameter of a fuzzy tennis ball), leading to uncertainty greater than the instrument’s precision.
Example of Estimating Uncertainty
- Meter Stick: When using a meter stick to measure the diameter of a tennis ball, you might estimate the uncertainty to be ±5mm, largely due to parallax errors when reading the measurement.
- Vernier Caliper: Using a Vernier caliper, which offers finer precision, the uncertainty might be reduced to ±2mm. However, the uncertainty is now limited by factors such as the definition of the ball’s diameter.
In both examples, the uncertainty is larger than the smallest divisions marked on the measuring tool (e.g., 1 mm for the meter stick and 0.05 mm for the Vernier caliper), showing that other factors besides the instrument's resolution contribute to the overall uncertainty.
Reporting Uncertainty
When reporting a measurement with its uncertainty, it’s important to clearly communicate what the uncertainty represents. The format is typically:
Measurement = (measured value ± standard uncertainty) unit of measurement
The "± standard uncertainty" indicates an approximate 68% confidence interval, meaning that there is a 68% chance that the true value lies within this range, based on the normal distribution of possible errors.
Example:
Diameter of Tennis Ball:
Diameter = 6.7 ± 0.2cm
This notation tells us that the measured diameter is 6.7 cm, with an uncertainty of 0.2 cm, indicating that the true diameter is likely between 6.5 cm and 6.9 cm, with about 68% confidence.
In conclusion, the experimenter must evaluate and quantify the uncertainty based on all the influencing factors and report it in a way that accurately reflects the measurement's reliability.
Standard Deviation
The standard deviation is a statistical measure that quantifies the amount of variation or dispersion in a set of data points. It provides insight into how spread out the measurements are relative to the mean (average) value. Here's how to calculate the standard deviation for a sample of N measurements:Steps to Calculate Standard Deviation
Calculate the Mean:
- Sum all the measurements.
- Divide this sum by N to obtain the average, or mean (xˉ).
Determine Deviations:
- Subtract the mean (
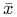 ) from each measurement to obtain N deviations (
) from each measurement to obtain N deviations (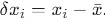 ).
).
- Subtract the mean (
Square the Deviations:
- Square each of these deviations.
Sum the Squared Deviations:
- Add all the squared deviations together.
Calculate the Variance:
- Divide the sum of the squared deviations by N − 1 to obtain the variance.
Find the Standard Deviation:
- Take the square root of the variance.
Formula for Standard Deviation
Let the N measurements be x1, x2,…,xN, and let the mean of these values be 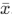 . The deviation for each measurement is given by
. The deviation for each measurement is given by 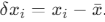 . The standard deviation s is calculated as follows:
. The standard deviation s is calculated as follows: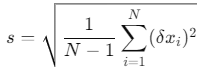
Where:
- s is the standard deviation.
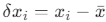 is the deviation of each measurement from the mean.
is the deviation of each measurement from the mean.- N is the total number of measurements.
Example Calculation
Let's consider a previous example where the average width 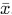 is 31.19 cm. Suppose the deviations of five measurements are:
is 31.19 cm. Suppose the deviations of five measurements are:
- 0.14 cm, 0.04 cm, 0.07 cm, 0.17 cm, and 0.01 cm
The standard deviation s can be calculated as:
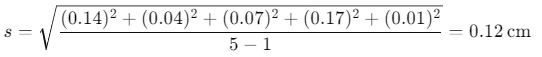
Significance of Standard Deviation
The standard deviation indicates the extent to which the individual measurements differ from the mean value. In the example, the standard deviation of 0.12 cm suggests that a new measurement using the same meter stick would likely fall within 0.12 cm of the estimated average of 31.19 cm, with about 68% confidence.- 68% Confidence Interval: Approximately 68% of measurements are expected to lie within one standard deviation
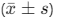 of the mean.
of the mean. - 95% Confidence Interval: Around 95% of measurements fall within two standard deviations (
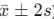 ) of the mean.
) of the mean. - 99.7% Confidence Interval: Nearly all measurements (99.7%) lie within three standard deviations
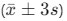 of the mean.
of the mean.
For a large number of measurements, the distribution of the data tends to follow a bell-shaped curve known as the Gaussian or Normal Distribution, where the standard deviation provides a measure of the spread of the data around the mean.
Standard Deviation of the Mean (Standard Error)
When reporting the average value of multiple measurements, the uncertainty associated with this average value is given by the standard deviation of the mean or standard error (SE). The standard error reflects the precision of the mean estimate derived from a sample of measurements.Formula for Standard Error
The standard error is calculated using the formula: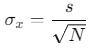
Where:
- σx is the standard error of the mean.
- s is the standard deviation of the sample.
- N is the number of measurements.
The standard error is smaller than the standard deviation by a factor of √N, reflecting that the uncertainty of the mean decreases with the number of measurements.
Example Calculation
In a previous example, the standard deviation s was 0.12 cm, and the number of measurements N was 5.
To find the standard error: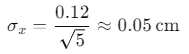 Thus, the average value should be reported as:
Thus, the average value should be reported as:
Average paper width = 31.19 ± 0.05cm
Anomalous Data
When analyzing data, it's crucial to examine the data set for patterns and outliers:- Patterns: Look for trends and consistency in the data.
- Outliers: Identify data points that deviate significantly from the general trend. Outliers might indicate significant phenomena or errors in the data.
Handling Anomalous Data:
- Investigate: Determine if an outlier is due to a mistake, random fluctuation, or an interesting anomaly.
- Justify: Do not discard extreme data points without proper justification. If the data point is justified as an error or outlier, it can be excluded to avoid skewing the average.
Fractional Uncertainty
The fractional uncertainty is the ratio of the uncertainty (standard error) to the average value. It provides a dimensionless measure of uncertainty and is often expressed as a percentage.Formula for Fractional Uncertainty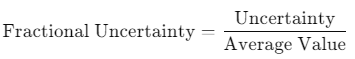 In the previous example:
In the previous example: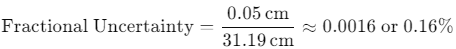
Interpreting Fractional Uncertainty:
- It represents how small the uncertainty is relative to the average value.
- It can be reported as a percentage or in parts per million (ppm).
- The fractional uncertainty is also crucial for propagating uncertainty in further calculations using the measurement result.
Significant Figures
Significant Figures are the digits in a number that carry meaningful information about its precision. They are crucial in scientific measurements to convey the accuracy of data.Defining Significant Figures
Non-Zero Digits: Always significant.
- Example: 123.45 has 5 significant figures.
Zeroes Between Non-Zero Digits: Always significant.
- Example: 1002 has 4 significant figures.
Leading Zeroes: Not significant. They only place the decimal point.
- Example: 0.0025 has 2 significant figures.
Trailing Zeroes in Decimal Numbers: Significant.
- Example: 12.50 has 4 significant figures.
Trailing Zeroes in Whole Numbers: Ambiguous without additional context. They may or may not be significant.
- Example: 1500 could have 2, 3, or 4 significant figures. To clarify, use scientific notation: 1.50 × 10³ (3 significant figures).
Using Calculators and Reporting
When using a calculator, results may show more digits than are meaningful based on the precision of the input values. Always round the final result to match the precision of the least precise measurement.Example: If you measure the radius of a circular field as 9 meters (1 significant figure) and calculate the area as A=πr2, the result from a calculator might be 254.4690049 m². Since the radius is only known to 1 significant figure, the area should be reported as 3×102 m² (1 significant figure).
Implications of Significant Figures
The number of significant figures in a reported value reflects the precision of the measurement and suggests an approximate relative uncertainty:1 Significant Figure: Implies a relative uncertainty of about 10% to 100%.
- Example: 9 (relative uncertainty ±1/9 ≈ ±11%).
2 Significant Figures: Implies a relative uncertainty of about 1% to 10%.
- Example: 99 (relative uncertainty ±1/99 ≈ ±1%).
3 Significant Figures: Implies a relative uncertainty of about 0.1% to 1%.
- Example: 100 (relative uncertainty ±1/100 = ±1%).
Note: For practical purposes, uncertainties in the last digit of significant figures can be approximated. The example with 99, implying ±1, highlights that the exact uncertainty can vary based on rounding conventions but gives a general sense of precision.
In summary, significant figures help in conveying the precision of measurements and ensure that calculations reflect the limitations of the data accurately.
Conclusion: Agreement of Measurements
In scientific and experimental contexts, determining whether measurements agree with each other or with theoretical predictions involves evaluating their uncertainty ranges. Here’s a concise overview:
Agreement with Theoretical Predictions:
- A measured result is considered to agree with a theoretical prediction if the theoretical value lies within the range of experimental uncertainty. This means the theoretical prediction falls within the interval defined by the measured value plus or minus its standard uncertainty.
Consistency Between Measurements:
- Two measured values are said to be consistent if their standard uncertainty ranges overlap. This means the range of uncertainty for each measurement includes the other measurement’s value. For instance, if Measurement A has an uncertainty range of A± uncertainty A and Measurement B has an uncertainty range of B± uncertainty B, the measurements are consistent if A is within ± uncertainty B and vice versa.
Discrepancy:
- If the uncertainty ranges of two measurements do not overlap, the measurements are considered discrepant, meaning they do not agree. This suggests that the difference between the two measurements exceeds the combined uncertainty ranges.
Avoiding Unethical Practices:
- It is essential to avoid inflating uncertainty ranges arbitrarily to make results appear consistent with expectations or other measurements. Such practices can lead to misleading conclusions. Instead, the focus should be on discussing the observed difference within the context of the measured uncertainty and exploring potential sources of discrepancy if the difference is significant.
In summary, agreement is determined by overlapping uncertainty ranges, while discrepancies arise when these ranges do not overlap. The interpretation should be grounded in the context of the uncertainties involved, and any significant discrepancies should be investigated to identify potential sources of error.
|
48 videos|57 docs|22 tests
|
FAQs on Error Analysis - Electrical and Electronic Measurements - Electrical Engineering (EE)
| 1. What is the difference between limiting errors and guarantee errors in error analysis in electrical engineering? |  |
| 2. How is the standard deviation used in error analysis for electrical engineering measurements? |  |
| 3. What is the significance of the standard deviation in error analysis for electrical engineering experiments? |  |
| 4. How can the standard error of the mean be calculated in error analysis for electrical engineering experiments? |  |
| 5. How can anomalous data be identified and addressed in error analysis for electrical engineering experiments? |  |
















