Unit Tests(Solutions): Rational Numbers | Mathematics (Maths) Class 8 PDF Download

Time: 1 hour  

M.M. 30  

Attempt all questions.  

Question numbers 1 to 5 carry 1 mark each.  

Question numbers 6 to 8 carry 2 marks each.  

Question numbers 9 to 11 carry 3 marks each.  

Question number 12 & 13 carry 5 marks each

Q1: The product of $\frac{2}{3}\backslash frac\{2\}\{3\}$ and $\frac{3}{4}\backslash frac\{3\}\{4\}$ is a rational number. (True/False) (1 Mark)
Ans: True
A rational number is any number that can be expressed as a fraction $\frac{p}{q}\backslash frac\{p\}\{q\}$, where $pp$ and $qq$ are integers, and $qq$ is not equal to zero.

The given problem involves multiplying two rational numbers:

$\frac{2}{3}\times \frac{3}{4}=\frac{6}{12}=\frac{1}{2}\backslash frac\{2\}\{3\}\; \backslash times\; \backslash frac\{3\}\{4\}\; =\; \backslash frac\{2\; \backslash times\; 3\}\{3\; \backslash times\; 4\}\; =\; \backslash frac\{6\}\{12\}\; =\; \backslash frac\{1\}\{2\}$

The result of this multiplication is $\frac{1}{2}\backslash frac\{1\}\{2\}$, which is a fraction, and hence a rational number.

Since both the numbers being multiplied are rational, their product is also a rational number. Therefore, the statement is True.

Q2: Write in standard form (lowest terms, positive denominator): 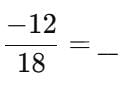(1 Mark)
Ans: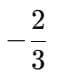

Q3: What is the multiplicative inverse of $-\frac{7}{9}-\backslash frac\{7\}\{9\}$? (1 Mark)
Ans: The multiplicative inverse is $-\frac{9}{7}-\backslash frac\{9\}\{7\}$.

Q4: Rational numbers are not closed under which operation? (1 Mark)
(i) Addition
(ii) Subtraction
(iii) Multiplication
(iv) Division
Ans: (iv) 
Division (because dividing by zero is not defined).

Q5: What is the additive identity of rational numbers? (1 Mark)
Ans: The additive identity of rational numbers is 0. When 0 is added to any rational number, the result is the number itself. For example, 5 + 0 = 5.

Q6: A wire of length $\frac{7}{4}\backslash frac\{7\}\{4\}$ meters is cut into two pieces. If one piece is $\frac{5}{8}\backslash frac\{5\}\{8\}$ meters long, how long is the other piece? (2 Marks)

Ans: Total length of wire = $\frac{7}{4}\backslash frac\{7\}\{4\}$ meters 

Length of one piece = $\frac{5}{8}\backslash frac\{5\}\{8\}$ meters 

Length of the other piece = $\frac{7}{4}-\frac{5}{8}\backslash frac\{7\}\{4\}\; -\; \backslash frac\{5\}\{8\}$$=\frac{9}{8}\backslash frac\{14\}\{8\}\; -\; \backslash frac\{5\}\{8\}\; =\; \backslash frac\{9\}\{8\}$ meters.

Q7: Verify if the rational numbers -3/4  and -8/5 are closed under multiplication. (2 Marks)
Ans: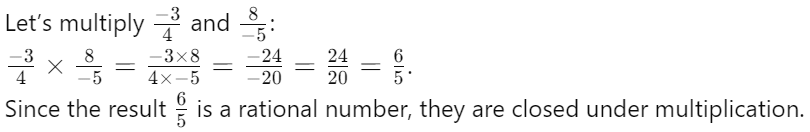

Q8: How does the associative property apply to the addition of rational numbers? (2 Marks)
Ans:
The associative property of addition states that the way in which numbers are grouped does not affect the sum. For rational numbers, $(a+b)+c=a+(b+c)(a\; +\; b)\; +\; c\; =\; a\; +\; (b\; +\; c)$. For example:
$(\frac{1}{2}+\frac{1}{3})+\frac{1}{4}=\frac{1}{2}+(\frac{1}{3}+\frac{1}{4})\backslash left(\backslash frac\{1\}\{2\}\; +\; \backslash frac\{1\}\{3\}\backslash right)\; +\; \backslash frac\{1\}\{4\}\; =\; \backslash frac\{1\}\{2\}\; +\; \backslash left(\backslash frac\{1\}\{3\}\; +\; \backslash frac\{1\}\{4\}\backslash right)$
Both sides will give the same sum, demonstrating the associative property.

Q9: (i) Simplify the expression $\frac{3}{5}+\frac{4}{7}\backslash frac\{3\}\{5\}\; +\; \backslash frac\{4\}\{7\}$ and express it as a single rational number. (3 Marks)
Ans:
Find a common denominator:

$LCM\; of\; 5\; and\; 7\; is\; 35.\; Convert\; both\; fractions:\frac{\mathrm{<img\; src="https://cn.edurev.in/ApplicationImages/Temp/23918212\_e8b7e4e1-9b82-4573-8a24-352ae962e608\_lg.png"\; style="display:\; block;\; margin:\; 5px\; auto;\; text-align:\; center;\; width:\; 475px;\; cursor:\; pointer;\; padding:\; 0px\; 1px;\; user-select:\; none;\; word-break:\; break-word;\; max-width:\; 100\%;\; letter-spacing:\; inherit;"\; alt="Unit\; Tests(Solutions):\; Rational\; Numbers\; |\; Mathematics\; (Maths)\; Class\; 8">}}{}\backslash text\{LCM\; of\; 5\; and\; 7\; is\; 35.\; Convert\; both\; fractions:\; \}\; \backslash frac\{3\}\{5\}\; =\; \backslash frac\{21\}\{35\},\; \backslash quad\; \backslash frac\{4\}\{7\}\; =\; \backslash frac\{20\}\{35$

So, the simplified expression is $\frac{41}{35}\backslash frac\{41\}\{35\}$.

(ii)  Match the following properties with their descriptions: 

Ans:
(i) - (b)
(ii) - (c)
(iii) - (a)

Q10: If $a=\frac{3}{8}a\; =\; \backslash frac\{3\}\{8\}$ and $b=\frac{2}{5}b\; =\; \backslash frac\{2\}\{5\}$, solve the expression $4a-3b+\frac{a}{b}4a\; -\; 3b\; +\; \backslash frac\{a\}\{b\}$. (3 Marks)
Ans: Substitute $a$ and $bb$ into the expression:

To simplify the expression, find a common denominator for the fractions:

For $\frac{3}{2}\backslash frac\{3\}\{2\}$, $\frac{6}{5}$, and $\frac{15}{16}\backslash frac\{15\}\{16\}$, the least common denominator (LCD) can be calculated as follows:

The denominators are 2, 5, and 16.

The LCD of 2, 5, and 16 is 80.
Convert each fraction to have the denominator of 80: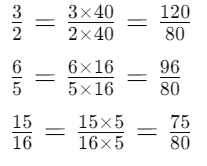

Now, substitute these values into the expression: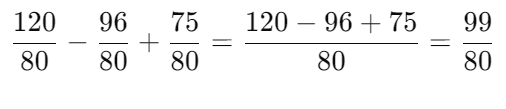
Q11: (i) Find any three rational numbers between $\frac{1}{3}\backslash dfrac\{1\}\{3\}$ and $\frac{1}{2}\backslash dfrac\{1\}\{2\}$. Show your working. (3 Marks)

 Ans: Make equal (larger) denominators so that numbers in between are visible.

$\frac{1}{3}=\frac{8}{24}, \frac{1}{2}=\frac{12}{24}$

Rational numbers strictly between $\frac{8}{24}\backslash dfrac\{8\}\{24\}$ and $\frac{12}{24}\backslash dfrac\{12\}\{24\}$  include:

$\frac{9}{24}=\frac{3}{8}, \frac{10}{24}=\frac{5}{12}, \frac{11}{24}\backslash dfrac\{9\}\{24\}=\backslash dfrac\{3\}\{8\},\backslash quad\; \backslash dfrac\{10\}\{24\}=\backslash dfrac\{5\}\{12\},\backslash quad\; \backslash dfrac\{11\}\{24\}$

Therefore, three rational numbers between $\frac{1}{3}\backslash dfrac\{1\}\{3\}$ and $\frac{1}{2}\backslash dfrac\{1\}\{2\}$ are
$\frac{3}{8},\frac{5}{12},\frac{11}{24}\backslash boxed\{\backslash dfrac\{3\}\{8\},\backslash \; \backslash dfrac\{5\}\{12\},\backslash \; \backslash dfrac\{11\}\{24\}\}$

$-13\; =\; 2x\; \backslash implies\; x\; =\; -\backslash frac\{13\}\{2\}\; =\; -6.5$

(ii) Prove that the sum of two rational numbers is always a rational number.

Ans: Let $\frac{a}{b}\backslash frac\{a\}\{b\}$ and $\frac{c}{d}\backslash frac\{c\}\{d\}$ be two rational numbers. Their sum is:

$\frac{a}{b}+\frac{c}{d}=\frac{a}{d}\backslash frac\{a\}\{b\}\; +\; \backslash frac\{c\}\{d\}\; =\; \backslash frac\{ad\; +\; bc\}\{bd\}$

Since $ad+bcad\; +\; bc$ and $b\mathrm{d }bd$are integers, and $bd\ne 0$, the result is a rational number.

Q12: If $x=\frac{3}{4}x\; =\; \backslash frac\{3\}\{4\}$ and $y=\frac{2}{3}y\; =\; \backslash frac\{2\}\{3\}$, solve the following expression: x+4y−2xy3x + 4y - 2xy. Show all steps. (5 Marks)

Answer:  Let's solve the expression $3x+4y-2xy3x\; +\; 4y\; -\; 2xy$ where $x=\frac{3}{4}x\; =\; \backslash frac\{3\}\{4\}$ and $y=\frac{2}{3}y\; =\; \backslash frac\{2\}\{3\}$

Calculate $3x3x$

$3x=3\times \frac{3}{4}=\frac{9}{4}3x\; =\; 3\; \backslash times\; \backslash frac\{3\}\{4\}\; =\; \backslash frac\{9\}\{4\}$

Calculate $4y4y$4y:

$4y=4\times \frac{2}{3}=\frac{8}{3}4y\; =\; 4\; \backslash times\; \backslash frac\{2\}\{3\}\; =\; \backslash frac\{8\}\{3\}$

Calculate $2xy2xy$:

$2xy=2\times \frac{3}{4}\times \frac{2}{3}=2\times \frac{6}{12}=2\times \frac{1}{2}=$1

Now, substitute these into the original expression:

$3x+4y-2xy=\frac{9}{4}+\frac{8}{3}-$1

Find a common denominator for $\frac{9}{4}\backslash frac\{9\}\{4\}$ and $\frac{8}{3}\backslash frac\{8\}\{3\}$:
The common denominator of 4 and 3 is 12.
Convert $\frac{9}{4}\backslash frac\{9\}\{4\}$to have a denominator of 12: $\frac{9}{4}=\frac{27}{12}\backslash frac\{9\}\{4\}\; =\; \backslash frac\{27\}\{12\}$
Convert $\frac{8}{3}\backslash frac\{8\}\{3\}$38 to have a denominator of 12: $\frac{8}{3}=\frac{32}{12}\backslash frac\{8\}\{3\}\; =\; \backslash frac\{32\}\{12\}$
Now add the fractions and subtract 1: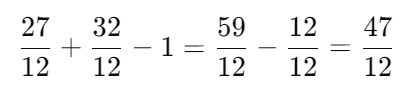

Final Answer: $3x+4y-2xy=\frac{47}{12}3x\; +\; 4y\; -\; 2xy\; =\; \backslash frac\{47\}\{12\}$

Q13: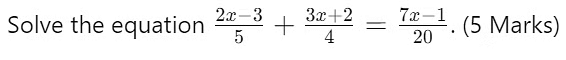

Ans: Find a common denominator for the left side:

The common denominator for 5 and 4 is 20.

Convert $\frac{2}{x}\backslash frac\{2x\; -\; 3\}\{5\}$ to have a denominator of 20:

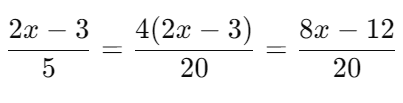
Convert $\frac{3}{x}\backslash frac\{3x\; +\; 2\}\{4\}$ to have a denominator of 20: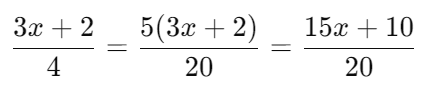

Combine the fractions on the left side: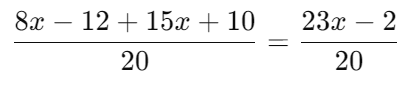
Now, the equation becomes:
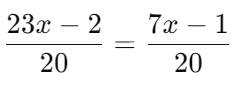Since the denominators are the same, set the numerators equal to each other:
23x−2=7x−1
23x−7x−2=−1
16x−2=−1
16x=1
x=1/16$x\; =\; \backslash frac\{1\}\{16\}$