Unit Test ( Solutions): Square and Square Roots | Mathematics (Maths) Class 8 PDF Download
Time: 1 hour
M.M.: 30
Attempt all questions.
Question numbers 1 to 5 carry 1 mark each.
Question numbers 6 to 8 carry 2 marks each.
Question numbers 9 to 11 carry 3 marks each.
Question numbers 12 & 13 carry 5 marks each.
Q1: A rectangular field has a length of 24 meters and a width of 7 meters. Calculate the diagonal of the field using the Pythagorean theorem and verify if the result is correct. (1 Mark)
Ans:
Diagonal = √(24² + 7²) = √(576 + 49) = √625 = 25 meters
Verification: 25² = 625, which confirms the calculation is correct.
Q2: Use the identity and find the square of 189. (1 Mark)
(a – b)2 = a2 – 2ab + b2
Ans:
189 = (200 – 11)2
= 40000 – 2 x 200 x 11 + 112
= 40000 – 4400 + 121
= 35721
Q3: The sum of the first 5 odd natural numbers is equal to the square of which number? (1 Mark)
(i) 2
(ii) 3
(iii) 4
(iv) 5
Ans: (iv)
The sum of the first 5 odd natural numbers is 1 + 3 + 5 + 7 + 9 = 25, which is equal to 5².
Q4: Find the number of non-square numbers between the squares of 10 and 11. (1 Mark)
(i) 21
(ii) 19
(iii) 20
(iv) 18
Ans: (iii)
There are 20 non-square numbers between 10² = 100 and 11² = 121.
Q5: The sum of two consecutive triangular numbers is a square number. Find the sum of 10 and 11 triangular numbers and verify this statement. (1 Mark)
Ans:
10th triangular number = 10(10+1)/2 = 55
11th triangular number = 11(11+1)/2 = 66
Sum = 55 + 66 = 121 = 11², which is a perfect square.
Q6: Find the smallest square number that is divisible by each of the numbers 8, 15 and 20. (2 Marks)
Ans:
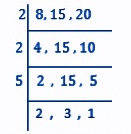
L.C.M of 8, 15 and 20 is (2×2×5×2×3) = 120.
120 = 2×2×3×5×2 = (2×2)×3×5×2
Here, 3, 5 and 2 cannot be paired.
Therefore, we need to multiply 120 by (3×5×2) i.e. 30 to get a perfect square.
Hence, the smallest squared number which is divisible by numbers 8, 15 and 20 = 120×30 = 3600
Q7: Show that the sum of two consecutive natural numbers is 132. (2 Marks)
Ans:
Let 2n + 1 = 13
So, n = 6
So, ( 2n + 1)2 = 4n2 + 4n + 1
= (2n2 + 2n) + (2n2 + 2n + 1)
Substitute n = 6,
(13)2 = ( 2 x 62 + 2 x 6) + (2 x 62 + 2 x 6 + 1)
= (72 + 12) + (72 + 12 + 1)
= 84 + 85
Q8: How many numbers lie between squares of the following numbers? (2 Marks)
(i) 12 and 13
(ii) 25 and 26
Ans: As we know, between n2 and (n+1)2, the number of non–perfect square numbers are 2n.
(i) Between 122 and 132 there are 2×12 = 24 natural numbers.
(ii) Between 252 and 262 there are 2×25 = 50 natural numbers.
Q9: Find the smallest whole number by which 1008 should be multiplied so as to get a perfect square number. Also, find the square root of the square number so obtained. (3 Marks)
Ans:
Let us factorise the number 1008.
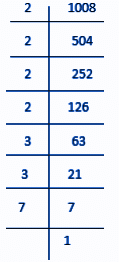
1008 = 2×2×2×2×3×3×7
= (2×2)×(2×2)×(3×3)×7
Here, 7 cannot be paired.
Therefore, we will multiply 1008 by 7 to get a perfect square.
New number so obtained = 1008×7 = 7056
Now, let us find the square root of 7056

7056 = 2×2×2×2×3×3×7×7
⇒ 7056 = (2×2)×(2×2)×(3×3)×(7×7)
⇒ 7056 = 22×22×32×72
⇒ 7056 = (2×2×3×7)2
Therefore;
⇒ √7056 = 2×2×3×7 = 84
Q10: Write a Pythagorean triplet whose one member is: (3 Marks)
(i) 6
(ii) 14
(iii) 16
(iv) 18
Ans:
We know, for any natural number m, 2m, m2–1, m2+1 is a Pythagorean triplet.
(i) 2m = 6
⇒ m = 6/2 = 3
m2–1= 32 – 1 = 9–1 = 8
m2+1= 32+1 = 9+1 = 10
Therefore, (6, 8, 10) is a Pythagorean triplet.
(ii) 2m = 14
⇒ m = 14/2 = 7
m2–1= 72–1 = 49–1 = 48
m2+1 = 72+1 = 49+1 = 50
Therefore, (14, 48, 50) is not a Pythagorean triplet.
(iii) 2m = 16
⇒ m = 16/2 = 8
m2–1 = 82–1 = 64–1 = 63
m2+ 1 = 82+1 = 64+1 = 65
Therefore, (16, 63, 65) is a Pythagorean triplet.
(iv) 2m = 18
⇒ m = 18/2 = 9
m2–1 = 92–1 = 81–1 = 80
m2+1 = 92+1 = 81+1 = 82
Therefore, (18, 80, 82) is a Pythagorean triplet.
Q11. Find the square roots of 100 and 169 by the method of repeated subtraction. (3 Marks)
Ans:
Let us find the square root of 100 first.
- 100 – 1 = 99
- 99 – 3 = 96
- 96 – 5 = 91
- 91 – 7 = 84
- 84 – 9 = 75
- 75 – 11 = 64
- 64 – 13 = 51
- 51 – 15 = 36
- 36 – 17 = 19
- 19 – 19 = 0
Here, we have performed a subtraction ten times.
Therefore, √100 = 10
Now, the square root of 169:
- 169 – 1 = 168
- 168 – 3 = 165
- 165 – 5 = 160
- 160 – 7 = 153
- 153 – 9 = 144
- 144 – 11 = 133
- 133 – 13 = 120
- 120 – 15 = 105
- 105 – 17 = 88
- 88 – 19 = 69
- 69 – 21 = 48
- 48 – 23 = 25
- 25 – 25 = 0
Here, we have performed subtraction thirteen times.
Therefore, √169 = 13
Q12: 2025 plants are to be planted in a garden in such a way that each row contains as many plants as the number of rows. Find the number of rows and the number of plants in each row. (5 Marks)
Ans:
Let the number of rows be, x.
Therefore, the number of plants in each row = x.
Total many contributed by all the students = x×x = x2
Given, x2 = Rs.2025
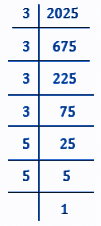
x2 = 3×3×3×3×5×5
⇒ x2 = (3×3)×(3×3)×(5×5)
⇒ x2 = (3×3×5)×(3×3×5)
⇒ x2 = 45×45
⇒ x = √(45×45)
⇒ x = 45
Therefore,
Number of rows = 45
Number of plants in each rows = 45
Q13: Find the least number which must be added to 1750 so as to get a perfect square. Also, find the square root of the obtained number. (5 Marks)
Ans:
Using long division method:
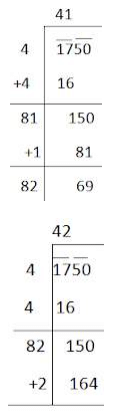
Here, (41)2 < 1750 > (42)2
We can say 1750 is ( 164 – 150 ) = 14 less than (42)2.
Therefore, if we add 14 to 1750, it will be a perfect square.
New number = 1750 + 14 = 1764
Therefore, the square root of 1764 is as follows:
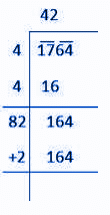
∴√1764 = 42
|
81 videos|423 docs|31 tests
|
FAQs on Unit Test ( Solutions): Square and Square Roots - Mathematics (Maths) Class 8
| 1. What is the difference between a square and a square root? |  |
| 2. How do you calculate the square of a number? |  |
| 3. What are some practical applications of square and square roots in daily life? |  |
| 4. Can you give examples of perfect squares? |  |
| 5. How can I find the square root of numbers that are not perfect squares? |  |

















