Unit Test (Solutions): Linear Equations in One Variable - Hobbies PDF Download

Time: 1 hour
 M.M.: 30 
Attempt all questions. 
Question numbers 1 to 5 carry 1 mark each. 
Question numbers 6 to 8 carry 2 marks each. 
Question numbers 9 to 11 carry 3 marks each.
Question numbers 12 & 13 carry 5 marks each.
Q1: Solve the following equation: 6x = x+15 (1 Mark)
(i)x=36
(ii)x=18
(iii)x=3
(iv)x=6

Ans: (iii)

Start with the given equation:
$3x\; =\; 2x\; +\; 18$6x = x+15

Subtract 2x from both sides:
6x−x = 15

Simplify the equation:
5x = 15

Thus, the solution is $x\; =\; 18$x = 3.

Q2: True or False: The solution to the equation $4z\; +\; 3\; =\; 6\; +\; 2z$4z + 3= 6 + 2z is $z\; =\; 2$z=2.(1 Mark)
Ans: False
$4z\; +\; 3\; =\; 6\; +\; 2z$4z+3=6+2z
Subtract $2z$2z from both sides:
$2z\; +\; 3\; =\; 6$2z+3=6
Subtract 3 from both sides:
$2z\; =\; 3$2z=3
Divide by 2:
$z\; =\; 1.5$z=1.5

Q3: The equation $4t\; -\; 7\; =\; 2t\; -\; 9$4t−7= 2t−9 has the solution: (1 Mark)
(a) t=−2
(b) $t\; =\; -1$t=−1
(c)$t\; =\; 1$t=1
(d) t=2

Ans:(b) 

Start with the given equation:
4t−7=2t−9
Move all terms involving $t$t to one side by subtracting $2t$2t from both sides:
$4t\; -\; 2t\; -\; 7\; =\; -9$4t−2t−7=−9
Simplify:
2t−7=−9

Add 7 to both sides to isolate the term with t:
$2t\; =\; -9\; +\; 7$2t=−9+7
Simplifying:
$2t\; =\; -2$2t=−2

Divide both sides by 2:
t=−2/2
t=−1

Q4: True or False: For the equation 2x−1 = 14−x, the solution is $x\; =\; 5$x=5.(1 Mark)

Ans: True
Solution: Add $xx$x to both sides:
$3x\; -\; 1\; =\; 14$3x−1=14
Add 1 to both sides:
$3x\; =\; 15$3x=15
Divide by 3:
x=5

Q5: The equation 3x−2=14−x has the solution: (1 Mark)
(i)x=5
(ii)$x\; =\; 4$x=4
(iii) $x\; =\; 6$x=6
(iv) $x\; =\; 3$x=3
Ans: (ii)

$x\; =$Start with the given equation:
3x−2=14−x

Add $\mathrm{<br>}x$x to both sides to move all terms involving $\mathrm{<br>}x$x to one side:
$3x\; +\; x\; -\; 2\; =\; 14$3x+x−2=14
Simplify:
$4x\; -\; 2\; =\; 14$4x−2=14

Add 2 to both sides:
$\mathrm{<br>}4x\; =\; 14\; +\; 2$4x=14+2
Simplify:
$4x\; =\; 16$4x=16

Divide both sides by 4:
$x=\frac{16}{4}x\; =\; \backslash frac\{16\}\{4\}$
$x=4x\; =\; 4$

So, the correct answer is $x\; =\; 4$x=4.

Q6: Solve and check the result: 2x−4 = 8 (2 Marks)

Ans:
Add 4 to both sides:
2x=8+4
2x=12

Divide by 2:
$x=\frac{12}{2}x\; =\; \backslash frac\{12\}\{2\}$
$x\; =\; 6$x=6

LHS =2(6)−4=12−4=8
RHS = 8, hence the solution is correct.

Q7: Simplify and solve: $4(t\; -\; 2)\; =\; 6(2t\; +\; 1)$4(t−2)=6(2t+1)(2 Marks)
Ans: Expand both sides:

$4t\; -\; 8\; =\; 12t\; +\; 6$4t − 8 = 12t + 6

Bring like terms together:

$-8\; -\; 6\; =\; 12t\; -\; 4t$−8 −6 = 12t − 4t

Divide both sides by 8: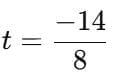

Simplify the fraction:

$t\; =\; \backslash frac\{-7\}\{4\}$

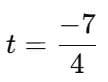
Q8:  The solution to the equation $x=\frac{4}{5}(x+10)x\; =\; \backslash frac\{4\}\{5\}(x\; +\; 10)$ is: (2 Marks)

Ans: 
Multiply both sides by 5:
$5x\; =\; 4(x\; +\; 10)$5x=4(x+10)
Expand:
$5x\; =\; 4x\; +\; 40$5x=4x+40
Subtract 4x from both sides:
$x\; =\; 40$x=40
Q9: Solve: $0.25(4f\; -\; 3)\; =\; 0.05(10f\; -\; 9)$0.25(4f−3) = 0.05(10f−9)(3 Marks)

Ans:
Expand both sides:
f−0.75=0.5f−0.45
Subtract $0.5f$0.5f from both sides:
$0.5f\; -\; 0.75\; =\; -0.45$0.5f−0.75=−0.45
Add $0.75$0.75 to both sides:
0.5f=0.3
Divide by 0.5:
$f\; =\; 0.6$f=0.6

Q10. Solve the following equation: 

$3y+\frac{4}{5}=\frac{29}{5}-y$

(3 Marks)

Ans: Start with the given equation:

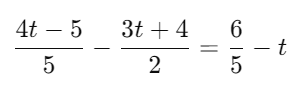Ans: 
Find the least common denominator (LCD) for the fractions. The LCD of 5 and 2 is 10. Multiply through by 10 to eliminate the fractions:$10\times \left(\frac{4}{t}\right)-10\times \left(\frac{3}{t}\right)=10\times (\frac{6}{5}-t)10\; \backslash times\; \backslash left(\; \backslash frac\{4t\; -\; 5\}\{5\}\; \backslash right)\; -\; 10\; \backslash times\; \backslash left(\; \backslash frac\{3t\; +\; 4\}\{2\}\; \backslash right)\; =\; 10\; \backslash times\; \backslash left(\; \backslash frac\{6\}\{5\}\; -\; t\; \backslash right)$

Simplifying:

$2(4t\; -\; 5)\; -\; 5(3t\; +\; 4)\; =\; 2(6)\; -\; 10t$2(4t−5)−5(3t+4)=2(6)−10t

Expand both sides:

$8t\; -\; 10\; -\; 15t\; -\; 20\; =\; 12\; -\; 10t$8t−10−15t−20=12−10t

Combine like terms:

(8t−15t)−10−20=12−10t

Simplifying further:

−7t−30=12−10t

Move all terms involving $tt$t to one side by adding $10t10t$10t to both sides:

$-7t\; +\; 10t\; -\; 30\; =\; 12$−7t+10t−30=12

Simplify:

$3t\; -\; 30\; =\; 12$3t−30=12

Add 30 to both sides:

$3t\; =\; 42$3t=42

Divide both sides by 3:

$t=\frac{42}{3}=14$

$t\; =\; 14$t=14

Q13: Solve the following equation: (5 Marks)

Ans:

Find the least common denominator (LCD). The LCD of 2 and 4 is 4. Multiply through by 4 to eliminate the fractions:

$\mathrm{<br>}$Simplifying:
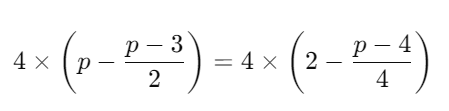
$4p\; -\; 2(p\; -\; 3)\; =\; 8\; -\; (p\; -\; 4)$4p−2(p−3)=8−(p−4)

Expand both sides:

$4p\; -\; 2p\; +\; 6\; =\; 8\; -\; p\; +\; 4$4p−2p+6=8−p+4

Combine like terms:

$(4p\; -\; 2p)\; +\; 6\; =\; 12\; -\; p$(4p−2p)+6=12−p

Simplifying further:

$2p\; +\; 6\; =\; 12\; -\; p$2p+6=12−p

Move all terms involving $pp$p to one side by adding $pp$p to both sides:

$2p\; +\; p\; +\; 6\; =\; 12$2p+p+6=12

Simplify:

$3p\; +\; 6\; =\; 12$3p+6=12

Subtract 6 from both sides:

$3p\; =\; 6$3p=6

Divide both sides by 3:

$p=\frac{6}{3}=2p\; =\; \backslash frac\{6\}\{3\}\; =\; 2$

$p\; =\; 2$p=2

$x\; =\; 9$