EduRev

Open App

Class 9 Exam > Class 9 Notes > Mathematics (Maths) Class 9 > Unit Test (Solutions): Polynomials

Unit Test (Solutions): Polynomials | Mathematics (Maths) Class 9 PDF Download

Time: 1 hour

M.M. 30

Attempt all questions.

Question numbers 1 to 5 carry 1 mark each.

Question numbers 6 to 8 carry 2 marks each.

Question numbers 9 to 11 carry 3 marks each.

Question number 12 & 13 carry 5 marks each

Q1: Which of the following is a polynomial in one variable? (1 Mark)

(i) $x^2 + \frac{1}{x}$

(ii) $2 x 2 + 3 x + 5$

(iii) $y 2 + x y$

(iv) 2/x + x

Ans: (ii)
A polynomial in one variable should not have any variable terms in the denominator or fractional exponents. It must have powers of a single variable with non-negative integers as exponents.

Option (i) is not a polynomial because $\frac{1}{x}$ includes a negative exponent.

Option (ii) is a polynomial in one variable $x$ , and it satisfies all conditions of a polynomial.

Option (iii) has two variables ( $y$ and $x$ ), so it’s not a polynomial in one variable.

Option (iv) contains $\frac{2}{x}$ , which has a negative exponent.

Q2: What is the degree of the polynomial $5 x 3 + 4 x 2 - x + 2$ ? (1 Mark)
(i) 1
(ii) 2
(iii) 3
(iv) 4

Ans: (iii)
The degree of a polynomial is the highest power (exponent) of the variable in the polynomial. In the polynomial $5 x 3 + 4 x 2 - x + 2$ 5x³+4x²−x+2, the highest power of $x$ is 3.
Thus, the degree of this polynomial is 3.

Q3: Which of the following is a zero of the polynomial $p (x) = x - 3$ ? (1 Mark)
(i) 1
(ii) 0
(iii) 3
(iv) -3

Ans: (iii)
A zero of a polynomial is a value of $x$ x that makes the polynomial equal to zero. To find the zero of $p (x) = x - 3$ , we set the polynomial equal to 0:

$x - 3 = 0$ $x = 3$
x=3

Thus, 3 is the zero of the polynomial.

Q4: What is the degree of the constant polynomial $7$ 7? (1 Mark)
(i) 0
(ii) 1
(iii) Not defined
(iv) 7

Ans: (i)
A constant polynomial is a polynomial with no variable terms (it is just a number). The degree of a constant polynomial is always 0 because there are no variables with exponents.
Thus, the degree of the constant polynomial $7$ 7 is 0.

Q5: The factor theorem states that $x - a$ x−a is a factor of the polynomial $p(x)$ p(x) if: (1 Mark)
(i) $p(a) = 1$ p(a)=1
(ii) $p(a) = a$ p(a)=a
(iii) $p(a) = 0$ p(a)=0
(iv) $p(a) \neq 0$

Ans: (c)
According to the factor theorem, $x - a$ is a factor of a polynomial $p (x)$ if and only if $p (a) = 0$ . This means that if you substitute $a$ into the polynomial and the result is zero, then $x - a$ is a factor of the polynomial.

Q6: Find the value of $k$ , if $x + 2$ is a factor of $p (x) = 3 x 3 + 2 x 2 - 5 x + k$ . (2 Marks)

Ans: Since $x + 2$ is a factor of $p (x)$ , by the Factor Theorem, $p (- 2) = 0$ .

Now, substitute $x = - 2$ into the polynomial $p (x) = 3 x 3 + 2 x 2 - 5 x + k$ :

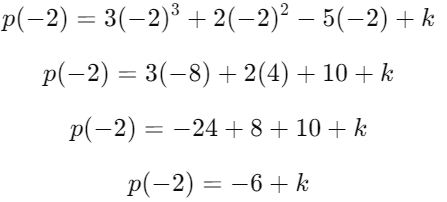
Unit Test (Solutions): Polynomials | Mathematics (Maths) Class 9

Since $p (- 2) = 0$ , we can set up the equation:

$- 6 + k = 0$

Solve for $k$ :

$k = 6$

Thus, the value of $k$ is 6.

Q7: Factorize the quadratic expression $4 x 2 + 7 x - 2.$ $(2 Marks)$ $4x^2 + 7x - 2$

Ans: To factorize the quadratic expression $4 x 2 + 7 x - 2$ , we need to split the middle term (7x) into two terms whose product is equal to $4 \times - 2 = - 8$ , and whose sum is equal to 7.

The two numbers that satisfy these conditions are 8 and -1 (since $8 \times -1 = -8$ and $8 + (- 1) = 7$ ).

So, we rewrite the expression as:

$4 x 2 + 8 x - x - 2$

Now, group the terms:

$(4 x 2 + 8 x) - (x + 2)$

Factor out the common terms:

$4 x (x + 2) - 1 (x + 2)$

Now, factor out $(x + 2)$ :

$(x + 2) (4 x - 1)$

Thus, the factorized form of $4 x 2 + 7 x - 2$ is:

$(x + 2) (4 x - 1)$

Q8: Evaluate $108 \times 109$ without multiplying directly.

Ans:

To evaluate $108 \times 109$ without direct multiplication, we can use the distributive property.

Rewrite the numbers:

108 \times 109 = (100 + 8) \times (100 + 9)

Apply the distributive property :

= 100^2 + (8 + 9) \times 100 + (8 \times 9)

Calculate each term:

$1002 = 10000$

$8 + 9 = 17$ so $17 \times 100 = 1700$

$8 \times 9 = 72$

Combine the results:

10000 + 1700 + 72 = 11772

Q9: Use the Factor Theorem to determine whether $g (x) = x - 2$ is a factor of $p (x) = 2 x 3 + x 2 - 2 x - 1$ . (3 Marks)

Ans:
To check if $g (x) = x - 2$ is a factor of $p (x) = 2 x 3 + x 2 - 2 x - 1$ using the Factor Theorem, we first evaluate $g (2)$ .

Evaluate $g (2)$ :

g (2) = 2 - 2 = 0

Since $g (2) = 0$ , $x - 2$ is a candidate for being a factor.

Perform polynomial long division of $p (x)$ by $g (x) = x - 2$ :

Divide the leading term $2 x 3$ by $x$ to get $2 x 2$ .
Multiply $2 x 2$ by $g (x)$ : $2 x 2 (x - 2) = 2 x 3 - 4 x 2$
Subtract this from $p (x)$ : $(2 x 3 + x 2 - 2 x - 1) - (2 x 3 - 4 x 2) = 5 x 2 - 2 x - 1$
Now, divide the leading term $5 x 2$ by $x$ to get $5 x$ .
Multiply $5 x$ by $g (x)$ : $5 x (x - 2) = 5 x 2 - 10 x$
Subtract: $(5 x 2 - 2 x - 1) - (5 x 2 - 10 x) = 8 x - 1$
Finally, divide $8 x 8$ by $x$ to get $8$ .
Multiply $8$ by $g (x)$ : $8 (x - 2) = 8 x - 16$
Subtract: $(8 x - 1) - (8 x - 16) = 15$

Since the remainder is $15$ 15, which is not $0$ 0, we conclude that $g (x) = x - 2$ is not a factor of $p (x)$ .
Q10: Expand $(5 x + 3 y - 4 z) 2$ .(3 Marks)
Ans:

Identify the terms:

(5 x + 3 y - 4 z) 2 = [5 x + 3 y + (- 4 z)] 2

Apply the expansion formula:

= (5 x) 2 + (3 y) 2 + (- 4 z) 2 + 2 (5 x) (3 y) + 2 (3 y) (- 4 z) + 2 (- 4 z) (5 x)

Calculate each term:

$(5 x) 2 = 25 x 2$

$(3 y) 2 = 9 y 2$

$(- 4 z) 2 = 16 z 2$

$2 (5 x) (3 y) = 30 x y$

$2 (3 y) (- 4 z) = - 24 y z$

$2 (- 4 z) (5 x) = - 40 z x$

Combine the results:

25 x 2 + 9 y 2 + 16 z 2 + 30 x y - 24 y z - 40 z x

Q11: If $a + b + c = 0$ , show that $a 3 + b 3 + c 3 = 3 a b c$ (3 Marks)
$Ans:$

Given the condition $a + b + c = 0$ , we can use the identity for the sum of cubes:

a 3 + b 3 + c 3 - 3 a b c = (a + b + c) (a 2 + b 2 + c 2 - a b - a c - b c)

Since $a + b + c = 0$ , we can substitute this into the identity:

a^3 + b^3 + c^3 - 3abc = 0 \cdot (a^2 + b^2 + c^2 - ab - ac - bc)

This simplifies to:

a 3 + b 3 + c 3 - 3 a b c = 0

Thus, we can conclude that:

a 3 + b 3 + c 3 = 3 a b c

Q12: Calculate the perimeter of a rectangle whose area is 25x² – 35x + 12. (5 Marks)

Ans:

Given,

Area of rectangle = 25x² – 35x + 12

We know, area of rectangle = length × breadth

So, by factoring 25x² – 35x + 12, the length and breadth can be obtained.

25x² – 35x + 12 = 25x²– 15x – 20x + 12

=> 25x² – 35x + 12 = 5x(5x – 3) – 4(5x – 3)

=> 25x² – 35x + 12 = (5x – 3)(5x – 4)

So, the length and breadth are (5x – 3)(5x – 4).

Now, perimeter = 2(length + breadth)

So, perimeter of the rectangle = 2[(5x – 3)+(5x – 4)]

= 2(5x – 3 + 5x – 4) = 2(10x – 7) = 20x – 14

So, the perimeter = 20x – 14

Q13: Factorize $4 x 2 + 2 y 2 + z 2 - 4 x y - 4 y z + 4 x z$ (5 Marks)
Ans:

To factor the expression $4 x 2 + 2 y 2 + z 2 - 4 x y - 4 y z + 4 x z$ , we can rearrange and group the terms.

Rearranging the expression:

4 x 2 - 4 x y + 4 x z + 2 y 2 - 4 y z + z 2

Group terms:

= (4 x 2 - 4 x y + 4 x z) + (2 y 2 - 4 y z + z 2)

Factor out common terms from each group:

From $4 x 2 - 4 x y + 4 x z$ , factor out 4: $= 4 (x 2 - x y + x z)$

From $2 y 2 - 4 y z + z 2$ , we can rearrange and factor:

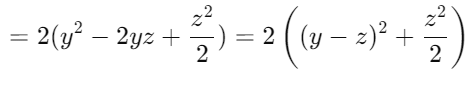
Unit Test (Solutions): Polynomials | Mathematics (Maths) Class 9
Putting it together: =4(x²−xy+xz)+2(y²−2yz+z²)

Factoring further:

Notice $x 2 - x y + x z$ can be recognized as: $= (x - y) (x + z)$

And for $y 2 - 2 y z + z 2$ : $= (y - z) 2$ ^{= (y - z)^2}

Finally, we can express the entire factorization as:

= (2 (x - y + z)) (x + (y - z))

The document Unit Test (Solutions): Polynomials | Mathematics (Maths) Class 9 is a part of the Class 9 Course Mathematics (Maths) Class 9.

All you need of Class 9 at this link: Class 9

	Mathematics (Maths) Class 9 40 videos\|560 docs\|57 tests

Mathematics (Maths) Class 9

40 videos|560 docs|57 tests

Join Course for Free

FAQs on Unit Test (Solutions): Polynomials - Mathematics (Maths) Class 9

1. What is a polynomial and how is it defined?

Ans. A polynomial is a mathematical expression that consists of variables raised to non-negative integer powers and coefficients. It is typically written in the form $ a_n x^n + a_{n-1} x^{n-1} + ... + a_1 x + a_0 $, where $ a_n, a_{n-1}, ..., a_0 $ are constants (coefficients), $ x $ is the variable, and $ n $ is a non-negative integer that represents the degree of the polynomial.

2. How do you add and subtract polynomials?

Ans. To add or subtract polynomials, combine like terms. Like terms are terms that have the same variable raised to the same power. For example, to add $ (3x^2 + 4x + 5) + (2x^2 + 3) $, you add the coefficients of like terms: $ (3x^2 + 2x^2) + 4x + (5 + 3) = 5x^2 + 4x + 8 $.

3. What is the difference between a monomial, binomial, and trinomial?

Ans. A monomial is a polynomial with just one term, such as $ 3x^2 $. A binomial has two terms, like $ 4x + 5 $. A trinomial consists of three terms, for example, $ x^2 + 2x + 1 $. The number of terms distinguishes these types of polynomials.

4. How can polynomials be factored?

Ans. Polynomials can be factored by finding their greatest common factor (GCF) or by using methods such as grouping, the difference of squares, or special factoring formulas (like $ a^2 - b^2 = (a - b)(a + b) $). For example, the polynomial $ x^2 - 9 $ can be factored as $ (x - 3)(x + 3) $.

5. What are the methods to solve polynomial equations?

Ans. Polynomial equations can be solved using various methods, such as factoring, using the quadratic formula (for second-degree polynomials), synthetic division, or numerical methods like the Newton-Raphson method for higher-degree polynomials. Each method is chosen based on the degree and complexity of the polynomial.

About this Document

1.3K Views

4.92/5 Rating

Sep 02, 2025 Last updated

Related Exams

Hobbies

Document Description: Unit Test (Solutions): Polynomials for Class 9 2025 is part of Mathematics (Maths) Class 9 preparation. The notes and questions for Unit Test (Solutions): Polynomials have been prepared according to the Class 9 exam syllabus. Information about Unit Test (Solutions): Polynomials covers topics like and Unit Test (Solutions): Polynomials Example, for Class 9 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Unit Test (Solutions): Polynomials.

Introduction of Unit Test (Solutions): Polynomials in English is available as part of our Mathematics (Maths) Class 9 for Class 9 & Unit Test (Solutions): Polynomials in Hindi for Mathematics (Maths) Class 9 course. Download more important topics related with notes, lectures and mock test series for Class 9 Exam by signing up for free. Class 9: Unit Test (Solutions): Polynomials | Mathematics (Maths) Class 9

Description

Full syllabus notes, lecture & questions for Unit Test (Solutions): Polynomials | Mathematics (Maths) Class 9 - Class 9 | Plus excerises question with solution to help you revise complete syllabus for Mathematics (Maths) Class 9 | Best notes, free PDF download

Information about Unit Test (Solutions): Polynomials

In this doc you can find the meaning of Unit Test (Solutions): Polynomials defined & explained in the simplest way possible. Besides explaining types of Unit Test (Solutions): Polynomials theory, EduRev gives you an ample number of questions to practice Unit Test (Solutions): Polynomials tests, examples and also practice Class 9 tests

	Mathematics (Maths) Class 9 40 videos\|560 docs\|57 tests

Mathematics (Maths) Class 9

40 videos|560 docs|57 tests

Join Course for Free

Download as PDF

Explore Courses for Class 9 exam

Viva Questions

practice quizzes

Important questions

Extra Questions

Previous Year Questions with Solutions

pdf

Semester Notes

ppt

Objective type Questions

video lectures

Unit Test (Solutions): Polynomials | Mathematics (Maths) Class 9

Summary

shortcuts and tricks

Unit Test (Solutions): Polynomials | Mathematics (Maths) Class 9

mock tests for examination

past year papers

MCQs

Exam

Unit Test (Solutions): Polynomials | Mathematics (Maths) Class 9

Sample Paper

study material

Free

;

Additional Information about Unit Test (Solutions): Polynomials for Class 9 Preparation

Unit Test (Solutions): Polynomials Free PDF Download

The Unit Test (Solutions): Polynomials is an invaluable resource that delves deep into the core of the Class 9 exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the Unit Test (Solutions): Polynomials now and kickstart your journey towards success in the Class 9 exam.

Importance of Unit Test (Solutions): Polynomials

The importance of Unit Test (Solutions): Polynomials cannot be overstated, especially for Class 9 aspirants. This document holds the key to success in the Class 9 exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

Unit Test (Solutions): Polynomials Notes

Unit Test (Solutions): Polynomials Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to Unit Test (Solutions): Polynomials. It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, Unit Test (Solutions): Polynomials Notes on EduRev are your ultimate resource for success.

Unit Test (Solutions): Polynomials Class 9 Questions

The "Unit Test (Solutions): Polynomials Class 9 Questions" guide is a valuable resource for all aspiring students preparing for the Class 9 exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study Unit Test (Solutions): Polynomials on the App

Students of Class 9 can study Unit Test (Solutions): Polynomials alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the Unit Test (Solutions): Polynomials, students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of Unit Test (Solutions): Polynomials is prepared as per the latest Class 9 syllabus.

Education Revolution