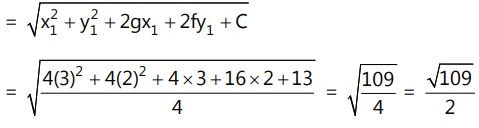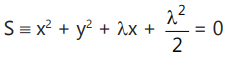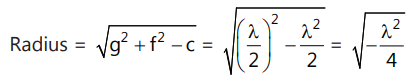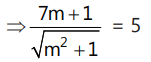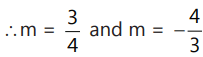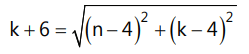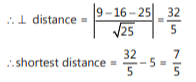Revision Notes: Circles | Mathematics (Maths) for JEE Main & Advanced PDF Download
 Important Formulas
Important Formulas
1. General equation of a circle: x² + y² + 2gx + 2fy + c = 0
(i) Centre of the circle = (-g, -f).
g = (1/2) × coefficient of x
f = (1/2) × coefficient of y
(ii)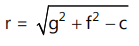 2. The equation ax² + 2hxy + by² + 2gx + 2fy + c = 0 represents a circle if:
2. The equation ax² + 2hxy + by² + 2gx + 2fy + c = 0 represents a circle if:
(i) a = b ≠ 0
(ii) h = 0
(iii) Δ = abc + 2hgf - af² - bg² - ch² ≠ 0
(iv) g² + f² - c ≥ 0
3. If the center of the circle is (h, k) and the radius is r, then the equation of the circle is:
(x - h)² + (y - k)² = r²
4. The equation of the circle drawn on the straight line joining two given points (x₁, y₁) and (x₂, y₂) as the diameter is:
(x - x₁)(x - x₂) + (y - y₁)(y - y₂) = 0
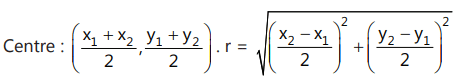 5.(i) In Parametric Form:
5.(i) In Parametric Form:
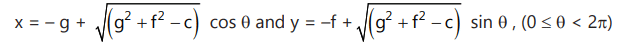 6. (i) Circle passing through three non-collinear points
6. (i) Circle passing through three non-collinear points
A(x₁, y₁), B(x₂, y₂), C(x₃, y₃) is represented by:
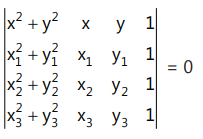 7. Circle circumscribing the triangle formed by the lines
7. Circle circumscribing the triangle formed by the lines
a₁x + b₁y + c₁ = 0 (i = 1,2,3):
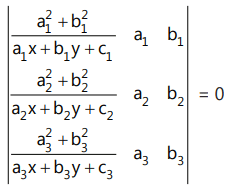
8. Intercepts length made by the circle on the X and Y axes are 2√(g² - c) and 2√(f² - c) respectively.
9. The position of a point (x₁, y₁) lies outside, on, or inside a circle, S ≡ x² + y² + 2gx + 2fy + c = 0.
When S₁ ≡ x₁² + y₁² + 2gx₁ + 2fy₁ + c = 0, respectively.
10. The power of P(x₁, y₁) w.r.t. S ≡ x² + y² + 2gx + 2fy + c = 0 is equal to PA.PB = PC.PD = PT² = square of the length of a tangent.
Where S₁ = x₁² + y₁² + 2gx₁ + 2fy₁ + c
11. Intercept length cut off from the line y = mx + c by the circle is
 12. The equation of tangent at (x₁, y₁) to circle x² + y² + 2gx + 2fy + c = 0 is
12. The equation of tangent at (x₁, y₁) to circle x² + y² + 2gx + 2fy + c = 0 is
xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
13. The equation of the tangent at (a cosθ, a sinθ) is x cosθ + y sinθ = a
14. Condition for tangency:
The line y = mx + c is a tangent of the circle x² + y² = a² if c² = a²(1 + m²)
The point of contact of tangent y = mx ± a√(1 + m²) is
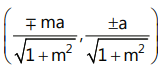 15. The length of the tangent from a point P(x₁, y₁) to the circle S = x² + y² + 2gx + 2fy + c = 0 is equal to
15. The length of the tangent from a point P(x₁, y₁) to the circle S = x² + y² + 2gx + 2fy + c = 0 is equal to
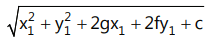
16. A pair of tangents from point (0, 0) to the circle are at right angles if g² + f² = 2c
17. Equation of the director circle of the circle x² + y² = a² is equal to x² + y² = 2a²
18. Equation of the director circle of circle x² + y² + 2gx + 2fy + c = 0 is
x² + y² + 2gx + 2fy + 2c - g² - f² = 0
19. The equation of normal at any point (x₁, y₁) to the circle x² + y² = a² is
x y₁ - x₁ y = 0 or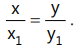 20. The equation of normal at (a cosθ, a sinθ) is y = x tan θ or y = mx
20. The equation of normal at (a cosθ, a sinθ) is y = x tan θ or y = mx
21. The equation of the chord of contact of tangents drawn from a point (x₁, y₁) to the circle x² + y² = a² is xx₁ + yy₁ = a²
To the circle x² + y² + 2gx + 2fy + c = 0 is xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
22. The area of Δ APQ is given by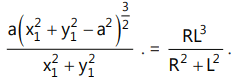 Where L & R are the length of the tangent and the radius of the circle.
Where L & R are the length of the tangent and the radius of the circle.

23. The equation of the chord of the circle x² + y² + 2gx + 2fy + c = 0, bisected at the point (x₁, y₁) is given as T = S₁,
i.e., xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = x₁² + y₁² + 2gx₁ + 2fy₁ + c.
24. The equation of the common chord of two circles x² + y² + 2g₁x + 2f₁y + c₁ = 0 and x² + y² + 2g₂x + 2f₂y + c₂ = 0 = 2x(g₁ - g₂) + 2y(f₁ - f₂) + c₁ - c₂ = 0 i.e., S₁ - S₂ = 0.
25. Length of the common chord: PQ = 2(PM) = 2√C1P2 - C1M2
Where,
C₁P = radius of the circle S₁ = 0
C₁M = perpendicular length from the center C₁ to the common chord PQ
26. Equation of the polar of the circle x² + y² + 2gx + 2fy + c = 0 and x² + y² = a²
w.r.t. (x₁, y₁) is:
xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
xx₁ + yy₁ - a² = 0, respectively.
27. The pole of the line lx + my + n = 0 with respect to the circle x² + y² = a² is:
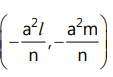
28. P(x₁, y₁) and Q(x₂, y₂) are conjugate points of the circle x² + y² + 2gx + 2fy + c = 0 when x₁x₂ + y₁y₂ + g(x₁ + x₂) + f(y₁ + y₂) + c = 0
If P and Q are conjugate points w.r.t. a circle with center at O and radius r, then
PQ² = OP² + OQ² - 2r².
29. P and T are the intersection points of direct common tangents and transverse common tangents, respectively.
They divide the line joining the centers of the circles externally and internally in the ratio of their radii.

Hence, the ordinates of P and T are:
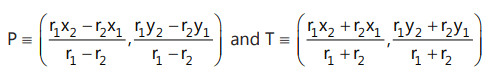
30. If two circles S ≡ x² + y² + 2g₁x + 2f₁y + c₁ = 0 and S' ≡ x² + y² + 2g₂x + 2f₂y + c₂ = 0 of r₁, r₂ and d be the distance between their centers,
then the angle of intersection (θ) between them is given by:
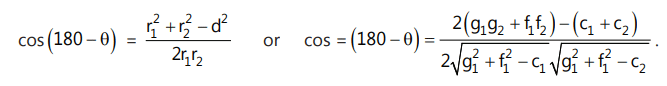
31. Condition for orthogonality: 2g₁g₂ + 2f₁f₂ = c₁ + c₂
32. S₁ - S₂ = 0 is the equation of the radical axis of the two circles. i.e., 2x (g₁ - g₂) + 2y (f₁ - f₂) + c₁ - c₂ = 0, which is a straight line.
33. The two limiting points of the given co-axial system are (√c , 0) and (-√c , 0).
34. If two limiting points of a coaxial system of circles are (a, b) and (α, β), then S₁ + λS₂ = 0, λ ≠ -1
or
(x - a)² + (y - b)² + λ[(x - α)² + (y - β)²] = 0, λ ≠ -1 is the coaxial system of circles.
35. If the origin is a limiting point of the coaxial system containing the circle x² + y² + 2gx + 2fy + c = 0, then the other limiting point is:
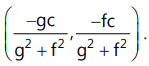
Solved Examples
Que 1: Find the equation of the circle whose centre lies on the line 2x - y - 3 = 0 and which passes through the points (3, -2) and (-2, 0).Ans: x² + y² + 3x + 12y + 2 = 0
Sol: Centre lies on 2x - y - 3 = 0
Let the centre be C = (h, 2h - 3)
It also passes through A = (3, -2) and B = (-2, 0)
Since AC = BC,
⇒ (h - 3)² + (2h - 1)² = (h + 2)² + (2h - 3)²
Expanding:
⇒ h² - 6h + 9 + 4h² - 4h + 1 = h² + 4h + 4 + 4h² - 12h + 9 - 2h + 3
Simplifying:Equation of the circle:
(x - h)² + (y - k)² = R²Expanding:
⇒ x² + 3x + 9/4 + y² + 12y + 36 = 81/4 + 16
Simplifying:
⇒ x² + y² + 3x + 12y + 2 = 0
Que 2: Find the length of the tangent drawn from the point (3, 2) to the circle 4x² + 4y² + 4x + 16y + 13 = 0
Ans: 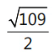
Sol: Length of tangent from a point
Que 3: The equation 2x² + 2y² + 2λ x + λ² = 0 represents a circle for:
(a) Each real value of λ
(b) No real value of λ
(c) Positive λ
(d) Negative λ
Ans: (b)
Sol:
∴ Radius is not defined for any real value of λ
Que 4: The radii of the circle x² + y² = 1, x² + y² - 2x - 6y = 6 and x² + y² - 4x - 12y = 9 are in
(a) A.P.
(b) G.P.
(c) H.P.
(d) None of these
Ans: (a)
Sol:
S₁ : x² + y² = 1
S₂ : x² + y² - 2x - 6y = 6
S₃ : x² + y² - 4x - 12y = 9
∴ r₁, r₂, r₃ are in A.P.
Que 5: Four unit circles pass through the origin and have their centres on the coordinate axes. The area of the quadrilateral whose vertices are the points of intersection (in pairs) of the circle, is
(a) 1 sq. unit
(b) 2√2 sq. units
(c) 4 sq. units
(d) Cannot be uniquely determined, insufficient data
Ans: (c)
Sol:
In this Question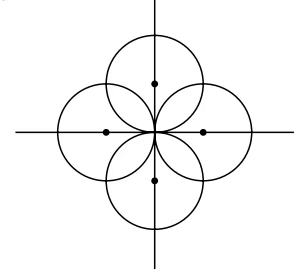
Since the centres lie on coordinate axes
The centres are (1, 0), (-1, 0), (0, 1), (0, -1)
Consider two circles with centres (1, 0) & (0, 1)
Their point of intersection will lie on the line y = x
Putting y = x in (x - 1)² + y² = 1
⇒ 2x² - 2x = 0
⇒ x = 1 & y = 1 (ignoring x = y = 0)
(1, 1) is the point
By symmetry, the other 3 points are
(1, -1), (-1, 1), (-1, -1)
It is a square of side 2 units
Area = 4 sq. units
Que 6: The angle between the two tangents from the origin to the circle (x -7)² + (y + 1)² = 25 equals
(a) π/6
(b) π/3
(c) π/2
(d) π/4
Ans: (c)
Sol: Let tangent from origin be y = mx
Using the condition of tangency, we get
(7m + 1)² = 25(m² + 1)
⇒ 24m² + 14m - 24 = 0
⇒ 12m² + 7m - 12 = 0
⇒ 12m² + 16m - 9m - 12 = 0
(4m - 3) (3m + 4)
The angle between tangents = π/2
Que 7: The equation of the circle passing through the foci of the ellipse x²/16 + y²/9 = 1, and having centre at (0,3) is (2013)
(a) x² + y² - 6y + 7 = 0
(b) x² + y² - 6y - 5 = 0
(c) x² + y² - 6y + 5 = 0
(d) x² + y² - 6y - 7 = 0
Ans: (d)
Sol:
to is (±√7,0)
Circle having centre as (0,3)
(x² + (y - 3)² = r² passes through focus, then
(±√7)² + (0 - 3)² = r²
7 + 9 = r²
⇒ r² = 16
⇒ x² + (y - 3)² = 16
⇒ x² + y² - 6y - 7 = 0
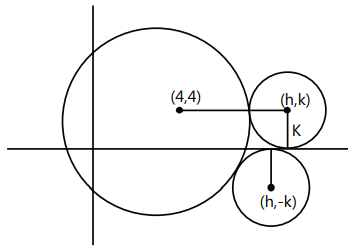
Q8: The centers of those circles which touch the circle, x² + y² - 8x - 8y - 4 = 0, externally and also touch the x-axis, lie on: (2016)
(a) An ellipse which is not a circle
(b) A hyperbola
(c) A parabola
(d) A circle
Ans: (c)
Sol: x² + y² - 8x - 8y - 4 = 0
Rewriting in standard form:
(x - 4)² + (y - 4)² = 36
Since the circles touch each other externally:
Squaring both sides:
k² + 36 + 12k = n² + 16 - 3h + k² - 3k + 16
Rearranging:
h² - 3h - 9 = 20k
⇒ x² - 3x - 20y - 4 = 0
If y < 0,(-k + 6)² = (n - 4)² + (k - 4)²
Expanding:
h² - 8h + 4k - 4 = 0
Rewriting:
x² - 8x + 4y - 4 = 0
Thus, the locus is a Parabola.
Que 9: Number of points in which the graphs of |y| = x + 1 and (x - 1)² + y² = 4 intersect, is
(a) 1
(b) 2
(c) 3
(d) 4
Ans: (c)
Sol: |y| = x + 1 & (x - 1)² + y² = 4
Substituting value of |y|
(x - 1)² + (x + 1)² = 4
Expanding:
x² = 1
Solving:
x = ±1
For x = -1, y = 0
For x = +1, |y| = 2 ⇒ y = ±2
Thus, three possible solutions are possible.
Que 10: The shortest distance from the line 3x + 4y = 25 to the circle x² + y² = 6x - 8y is equal to
(a) 7/5
(b) 9/5
(c) 11/5
(d) 32/5
Ans: (a)
Sol: Shortest distance from line to circle = ⊥ distance - radius
Centre of circle = (3, -4) & radius = 5
|
176 videos|582 docs|160 tests
|
FAQs on Revision Notes: Circles - Mathematics (Maths) for JEE Main & Advanced
| 1. What are the key formulas related to circles that I should remember for JEE? |  |
| 2. How can I find the area of a sector of a circle? |  |
| 3. What is the relationship between the radius, diameter, and circumference of a circle? |  |
| 4. How do I determine if a point lies inside, on, or outside a circle? |  |
| 5. Can you explain the concept of tangents to a circle? |  |