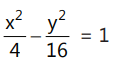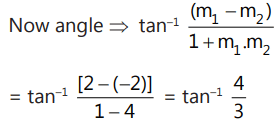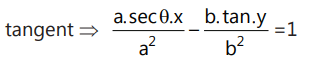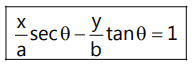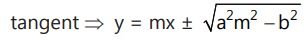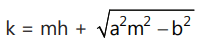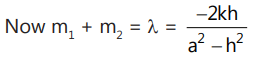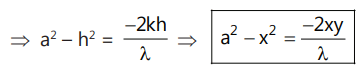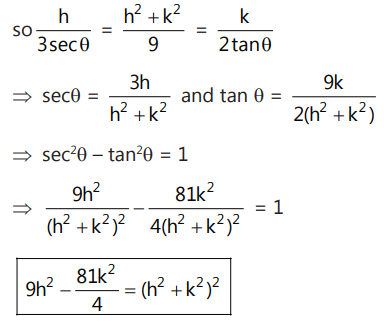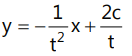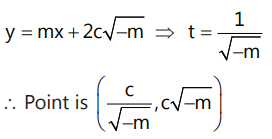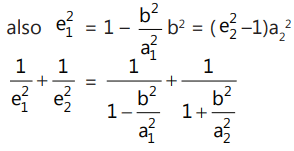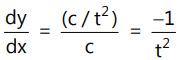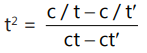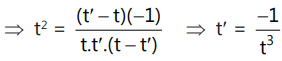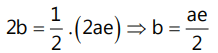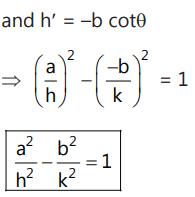Revision Notes: Hyperbola | Mathematics (Maths) for JEE Main & Advanced PDF Download

Important Formulas
(a) Standard Hyperbola:

Hyperbola
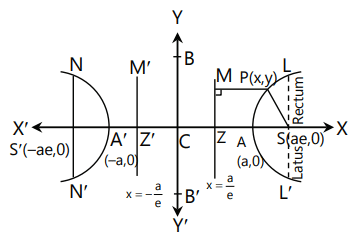
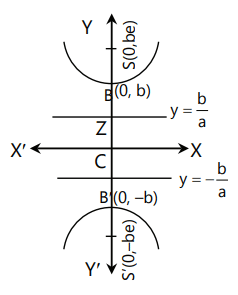
Conjugate Hyperbola
 (b) Special form of hyperbola: If (h , k) is the centre of a hyperbola and its axes are parallel to the co-ordinate axes, then the equation of the hyperbola is
(b) Special form of hyperbola: If (h , k) is the centre of a hyperbola and its axes are parallel to the co-ordinate axes, then the equation of the hyperbola is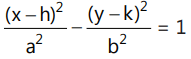
(c) Parametric equations of a hyperbola:The equation x = a sec φ and y = b tan φ are known as the parametric equation of the standard hyperbola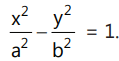
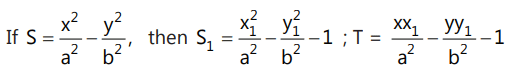
(d) Position of a point and a line w.r.t. a hyperbola: n The point (x1, y1) lies inside, on or outside the hyperbola 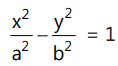 according to
according to The line y = mx + c intersects at 2 distinct points, 1 point, or does not intersect with the hyperbola according as c² >, =, or < a²m² - b².
The line y = mx + c intersects at 2 distinct points, 1 point, or does not intersect with the hyperbola according as c² >, =, or < a²m² - b².
(e) Tangent:
(i) Point form:
The equation of the tangent to the hyperbola
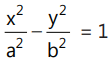
at (x₁, y₁) is:
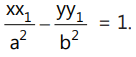
(ii) Parametric form:
The equation of the tangent to the hyperbola
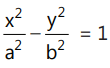
at parametric coordinates (a sec φ, b tan φ) is:
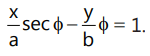
(iii) Slope form:
The equation of the tangents having slope m to the hyperbola
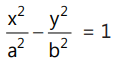
are:
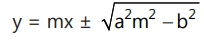
and the coordinates of points of contact are:

(f) Equation of a pair of tangents:
The equation of a pair of tangents from an external point (x₁, y₁) to the hyperbola
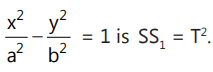
(g) Normal:
(i) Point form:
The equation of the normal to the hyperbola
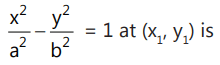
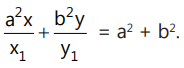
(ii) Parametric form:
The equation of the normal at parametric coordinates (a sec θ, b tan θ) to the hyperbola
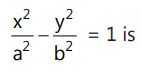
a x cos θ + b y cot θ = a² + b².
(iii) Slope form:
The equation of the normal having slope m to the hyperbola
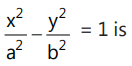
is:

(iv) Condition for normality:
The line y = mx + c is a normal to the hyperbola
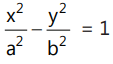
if:
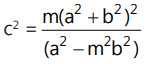
(v) Points of contact:
The coordinates of the points of contact are:
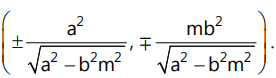
(h) Director Circle:
The equation of the director circle of the hyperbola
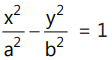
is given by: x² + y² = a² - b².
(i) Chord of Contact:
The equation of the chord of contact of the tangents drawn from the external point (x₁, y₁) to the hyperbola is given by:
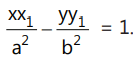
(j) Chord of the Hyperbola:
The equation of the chord of the hyperbola
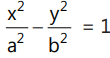
whose midpoint is (x₁, y₁) is T = S₁.
(k) Equation of a Chord:
The equation of a chord joining points P(a sec φ₁, b tan φ₁) and Q(a sec φ₂, b tan φ₂) is:
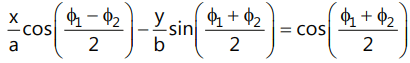
(l) Equation of the Polar:
The equation of the polar of the point (x₁, y₁) with respect to the hyperbola is given by T = 0.
The pole of the line lx + my + n = 0 with respect to the hyperbola

(m) Equation of a Diameter:
The equation of a diameter of the hyperbola
corresponding to the chords of slope m is:
(n) Conjugate Diameters:
The diameters y = m₁x and y = m₂x are conjugate if:
(o) Asymptotes:
- An asymptote to a curve touches the curve at infinity.
- The equation of the asymptotes of the hyperbola
- The asymptote of a hyperbola passes through the center of the hyperbola.
- The combined equation of the asymptotes of the hyperbola
- The angle between the asymptotes of
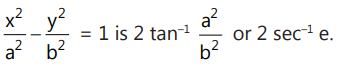
- A hyperbola and its conjugate hyperbola have the same asymptotes.
- The bisector of the angles between the asymptotes are the coordinate axes.
- Equation of the hyperbola - Equation of the asymptotes = constant.
(p) Rectangular or Equilateral Hyperbola:
- A hyperbola for which a = b is said to be a rectangular hyperbola, its equation is:x² - y² = a².
- xy = c² represents a rectangular hyperbola with asymptotes x = 0, y = 0.
- Eccentricity of a rectangular hyperbola is √2 and the angle between the asymptotes of a rectangular hyperbola is 90°.
- Parametric equation of the hyperbola xy = c² are: x = ct, y = c/t, where t is a parameter.
- Equation of a chord joining t₁, t₂ on xy = c² is:x + y t₁ t₂ = c(t₁ + t₂).
- Equation of a tangent at (x₁, y₁) to xy = c² is:
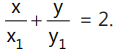
- Equation of a tangent at t is: x + y t² = 2ct.
- Equation of the normal at (x₁, y₁) to xy = c² is: x x₁ - y y₁ = x₁² - y₁².
- Equation of the normal at t on xy = c² is: x t³ - y t - c t⁴ + c = 0.
(i.e. Four normals can be drawn from a point to the hyperbola xy = c².) - If a triangle is inscribed in a rectangular hyperbola, then its orthocenter lies on the hyperbola.
- Equation of the chord of the hyperbola xy = c² whose middle point is given is T = S₁.
- Point of intersection of tangents at t₁ and t₂ to the hyperbola xy = c² is:
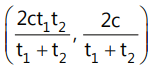
Problem-Solving Tactics
(a)In general convert the given hyperbola equation into the standard form 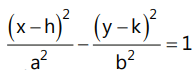 and compare it with
and compare it with 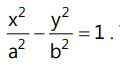 Then solve using the properties of the hyperbola
Then solve using the properties of the hyperbola
So, it is advised to remember the standard results.
(b)Most of the standard results of a hyperbola can be obtained from the results of an ellipse 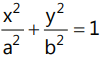 just by changing the sign of b2.
just by changing the sign of b2.
Solved Examples
Que 1: Find the acute angle between the asymptotes of 4x² - y² = 16.
Ans:
⇒ y = 2x and y = -2x
Que 2: Find the locus of the points of intersection of two tangents to a hyperbola 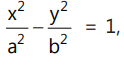 if the sum of their slopes is a constant λ.
if the sum of their slopes is a constant λ.
Ans:
Tangent passes through (h, k)
(k - mh)² = a²m² - b²
Expanding,
k² + m²h² - 2m . kh = a²m² - b²
Rearrange,
(a² - h²)m² + 2m . kh = - (b² + k²)
Que 3: Given a hyperbola 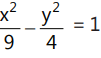 and a circle x² + y² = 9,Find the locus of the midpoint of the chord of contact drawn from a point on the hyperbola to the circle.
and a circle x² + y² = 9,Find the locus of the midpoint of the chord of contact drawn from a point on the hyperbola to the circle.
Ans:
Point on the hyperbola: (3 secθ, 2 tanθ)
Now, the equation of the chord of contact is:
hx + ky = h² + k²
And also, 3 secθ . x + 2 tanθ . y = 9
Que 4: If the straight line y = mx + 2c√-m touches the hyperbola xy = c², then the coordinates of the point of contact are (……………….)
Ans: Tangent to the hyperbola xy = c² at (ct, c/t) will be of the form:
Que 5: An ellipse and a hyperbola have the same center origin, the same foci, and the minor-axis of one is the same as the conjugate axis of the other. If e₁, e₂ are their eccentricities respectively, then:
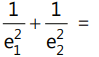
(a) 1
(b) 2
(c) 4
(d) None of these
Ans: (b)
Ellipse Hyperbola
Now, a₁e₁ = a₂e₂
… (i)
Also, we have:
a₁e₁ = a₂e₂
Expanding,
a₁² - b² = a₂² + b² ...........(ii)
Adding,
a₁² + a₂² = 2(a₂² + b²) ...........(iii)
Now, from equation (i),
Que 6: If the normal at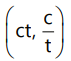 on the curve xy = c² meets the curve again at t', then:
on the curve xy = c² meets the curve again at t', then:
(a)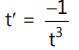
(b) 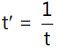
(c) 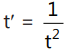
(d) 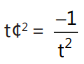
Ans: (a)
We have
So, normal slope = t²
Now,
We have
Que 7: The eccentricity of the hyperbola whose length of the latus rectum is equal to 8 and the length of its conjugate axis is equal to half of the distance between its foci, is: (2016)
(a) 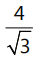 (b)
(b) 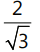 (c)
(c) 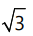 (d) 4/3
(d) 4/3
Ans: (b)
Que 8: Tangents at any point on the hyperbola 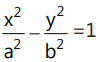 cut the axes at A and B respectively. If the rectangle OAPB (where O is the origin) is completed, then the locus of point P is given by:
cut the axes at A and B respectively. If the rectangle OAPB (where O is the origin) is completed, then the locus of point P is given by:
(a) 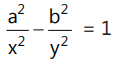 (b)
(b) 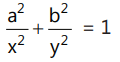 (c)
(c) 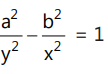 (d) None of these
(d) None of these
Ans: (a)
Equation of tangent
⇒ h = a cosθ
Que 9: P is a point on the hyperbola 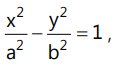 N is the foot of the perpendicular from P on the transverse axis.The tangent to the hyperbola at P meets the transverse axis at T.If O is the center of the hyperbola, then OT × ON is equal to:
N is the foot of the perpendicular from P on the transverse axis.The tangent to the hyperbola at P meets the transverse axis at T.If O is the center of the hyperbola, then OT × ON is equal to:
(a) e²
(b) a²
(c) b²
(d) b² / a²
Ans: (b)
We have NP = a secθ and the tangent slope is
So at y = 0,x = a cosθ
So, OT = a cosθ
Thus,
OT × ON = a cosθ × a secθ = a²
So, the correct answer is (b) a².
Que 10: Equation of a common tangent with a positive slope to the circle as well as to the hyperbola is:
(a) 2x - √5 y - 20 = 0
(b) 2x - √5 y + 4 = 0
(c) 3x - 4y + 8 = 0
(d) 4x - 3y + 4 = 0
Ans: Equation of tangents to the hyperbola having slope m is:
...........(i)
Equation of the tangent to the circle is:...........(ii)
Equations (i) and (ii) will be identical for m = 2/√5
Thus, the equation of the common tangent is:
2x - √5 y + 4 = 0
So, the correct answer is (b) 2x - √5 y + 4 = 0.
|
176 videos|588 docs|160 tests
|
FAQs on Revision Notes: Hyperbola - Mathematics (Maths) for JEE Main & Advanced
| 1. What is a hyperbola and how is it defined mathematically? |  |
| 2. What are the key features of a hyperbola that students should remember for JEE? |  |
| 3. How do you find the equations of the asymptotes for a hyperbola? |  |
| 4. What strategies can be used to solve hyperbola-related problems in JEE? |  |
| 5. Can you explain the significance of eccentricity in hyperbolas and how it's calculated? |  |