Important Formulas: Square Root & Cube Root | Quantitative Aptitude for Competitive Exams - SSC MTS / SSC GD PDF Download
| Table of contents |

|
| What is Square Root? |

|
| Methods to Find Square Root |

|
| What is Cube Root? |

|
| Methods to Find Cube Root |

|
| Square Root and Cube Root Table |

|
What is Square Root?
 The square root of a number x is a mathematical operation that provides the value which, when multiplied by itself, equals the number x. It is denoted as √x.
The square root of a number x is a mathematical operation that provides the value which, when multiplied by itself, equals the number x. It is denoted as √x.
The square root of a number can be either positive or negative, but typically the positive square root is used. For instance, the positive square root of 9 is 3, and the negative square root of 9 is -3.
Square Root Symbol
The square root of a number x is a value that, when multiplied by itself, results in the number x. The number x is considered a perfect square.
For example:
- 2² = 4, so the square root of 4 is 2.
- 3² = 9, so the square root of 9 is 3.
- 4² = 16, so the square root of 16 is 4.
The symbol for square root is √. Therefore:
- The square root of 4 is represented as √4 = 2.
- The square root of 9 is represented as √9 = 3, and so on.
Properties of Square Root
The properties of square roots are as follows:
- The square root of a perfect square is a rational number.
- The square root of a non-perfect square is an irrational number.
- The square root of an even perfect square is even.
- The square root of an odd perfect square is odd.
- A perfect square root exists only for a perfect square number.
- A perfect square cannot be negative, meaning the square root of a negative number is not defined.
Square Root Formula
The square root formula is used to determine the square root of a number. The exponent formula for a number 'x' is expressed as: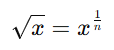
If n = 2, we call it the square root. Therefore, the square root of any number 'x' can be written using the formula: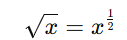
Methods to Find Square Root
The square root of a number can be found using different methods, including the prime factorization method, repeated subtraction method, and long division method. Let's explore each of these methods in detail.
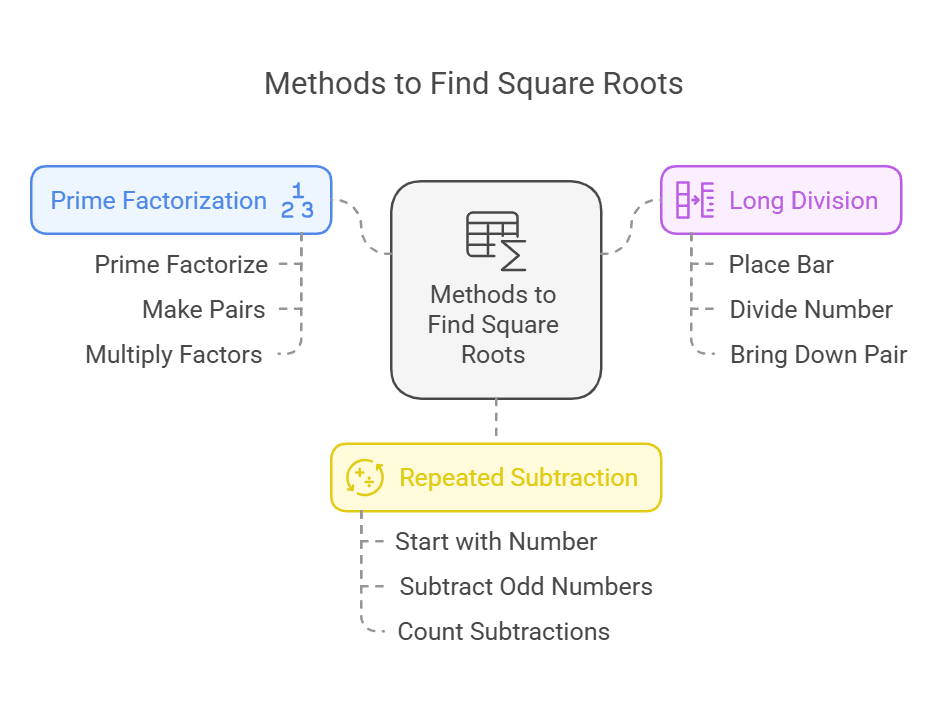
Method 1: Square Root by Prime Factorization Method
To find the square root using the prime factorization method, follow these steps:
- Step 1: Prime Factorize the Given Number: Break the number down into its prime factors.
- Step 2: Make Pairs of Same Prime Factors: Group the prime factors into pairs of identical numbers.
- Step 3: Take One Factor from Each Pair: For each pair, take one factor outside the radical sign (√).
- Step 4: Multiply All the Factors: Multiply all the factors obtained from the pairs to get the square root.
Example: Find the square root of 144.
Solution:
Steps:
- Prime Factorize the Given Number: 144 = 2 × 2 × 2 × 2 × 3 × 3 (or 144 = 24 × 32)
- Make Pairs of Same Prime Factors: (2 × 2) and (3 × 3)
- Take One Factor from Each Pair: 2 and 3
- Multiply All the Factors: 2 × 3 = 6
Result: The square root of 144 is 12.
Method 2: Square Root by Long Division Method
To find the square root using the long division method, follow these steps:
- Step 1: Place a Bar Over Every Pair of Digits: Start from the right-most side (units place) and group the digits into pairs.
- Step 2: Divide the Left-Most Number: Divide the left-most number by the largest number whose square is less than or equal to the number in the left-most pair.
- Step 3: Bring Down the Next Pair: Bring down the next pair of digits and add the last digit of the quotient to the divisor. Find a suitable number that, when added to the divisor, creates a new divisor for the dividend.
- Step 4: Repeat the Process: Continue the process to find the quotient, which will be the square root.
- Step 5: Continue with Decimals: If necessary, add decimal places by bringing down pairs of zeros and repeating the steps.
Example: Find the square root of 625.
Solution:
Steps:
- Place a Bar Over Every Pair of Digits: Group 62 and 5.
- Divide the Left-Most Number (62): The largest number whose square is less than or equal to 62 is 8 (since 82 = 64, but 72 = 49, which is less than 62). Start by dividing 62 by 7: 62 ÷ 7 = 8 (quotient)
- Bring Down the Next Pair (25): Now bring down the next pair (25) making the dividend 625.
- Repeat the Process: Add the quotient (8) to the divisor (7) to get 15. Divide 625 by 15, giving a quotient of 5.
- Final Result: The quotient is 25, which is the square root of 625.
Result: The square root of 625 is 25.
Method 3: Square Root by Repeated Subtraction Method
The repeated subtraction method works for perfect squares:
- Step 1: Start with the Number: Subtract consecutive odd numbers from the number starting from the given number.
- Step 2: Repeat Until You Reach Zero: Continue subtracting the next odd number until the result is zero.
- Step 3: The Number of Subtractions: The nth odd number at which the result becomes zero is the square root of the given number.
Example: Find the square root of 49.
Solution:
Steps:
- Start with the Number: Begin with 49.
- Subtract Consecutive Odd Numbers:
49 − 1 = 48
48 − 3 = 45
45 − 5 = 40
40 − 7 = 33
33 − 9 = 24
24 − 11 = 13
13 − 13 = 0 - Result: The 7th odd number subtracted is 49, and the square root of 49 is 7.
Result: The square root of 49 is 7.
What is Cube Root?
 The cube root of a number x is a mathematical operation that provides the value which, when multiplied by itself three times (or raised to the power of three), gives the original number x. The cube root of a number “x” is represented as ∛x.
The cube root of a number x is a mathematical operation that provides the value which, when multiplied by itself three times (or raised to the power of three), gives the original number x. The cube root of a number “x” is represented as ∛x.
For example, the cube root of 8 is 2, because 2 × 2 × 2 = 8, or ∛8 = 2. The cube root can also be negative for negative numbers.
Cube Root Symbol
The cube root of a number a is that number which, when multiplied by itself three times, gives the number ‘a’ itself.
For example:
- 23 = 8, or the cube root of 8 is 2
- 33 = 27, or the cube root of 27 is 3
- 43 = 64, or the cube root of 64 is 4
The symbol for the cube root is 1⁄3 or ∛3.
Thus, the cube root of 8 is represented as ∛8 = 2 and that of 27 is represented as ∛27 = 3, and so on.
Properties of Cube Root
The properties of cube roots are as follows:
- The cube root of all odd numbers is an odd number.
- The cube root of all even natural numbers is even.
- The cube root of a negative integer always results in a negative number.
- The cube root of a perfect cube is a rational number.
- The cube root of a non-perfect cube is an irrational number.
Cube Root Formula
The cube root formula is a mathematical expression used to calculate the cube root of a number. It helps in determining the cube root of any given number expressed in radical form using the symbol ∛.
Suppose x is any number such that x = y × y × y. Then, the formula for calculating the cube root is:
Cube root of x = 
Where y is the cube root of the number x.
Methods to Find Cube Root
The various methods to find the cube root include the prime factorization method, Halley's method, and others. Let's explore these methods in detail.
Method 1: Cube Root by Prime Factorization Method
To find the cube root using the prime factorization method, follow these steps:
- Step 1: Determine the prime factors of the given number.
- Step 2: For each prime factor, group them into sets of three.
- Step 3: Take one factor from each group and multiply all the factors together. If any factor cannot be grouped into sets of three, it cannot be simplified further.
Example: Find the cube root of 216.
Solution:
- Prime Factorization of 216: 216 = 2 × 2 × 2 × 3 × 3 × 3
- Group the prime factors in sets of three: (2 × 2 × 2) and (3 × 3 × 3)
- Take one factor from each group: 2 and 3
- Multiply the factors: 2 × 3 = 6
Result: The cube root of 216 is 6.
Method 2: Cube Root by Halley’s Method
Halley’s method is a root-finding technique used for functions with a single real variable and a continuous second derivative.
The formula for Halley’s method is: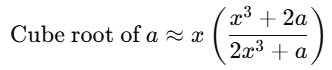 Where:
Where:
- a is the number whose cube root is being calculated.
- x is an initial guess for the cube root.
Example: Find the cube root of 27 using Halley’s method with an initial guess x = 3.
Solution:
Initial guess: x = 3
Apply Halley’s method formula: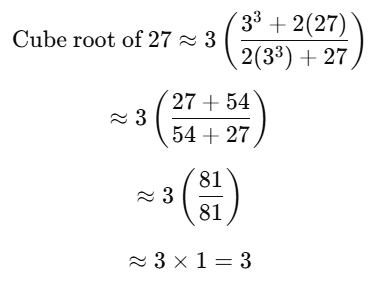
Result: The cube root of 27 is approximately 3.
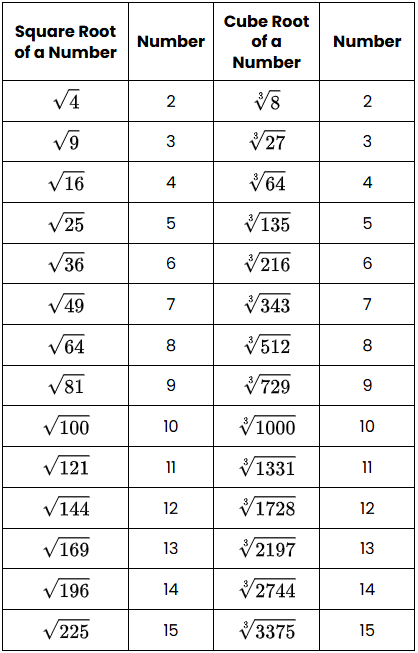
Square Root and Cube Root Table
|
203 videos|110 docs|114 tests
|















