Proof of Theorems: Quadrilaterals | Mathematics (Maths) Class 9 PDF Download
Theorem 1: A diagonal of a parallelogram divides it into two congruent triangles.
Proof: Consider parallelogram ABCD with diagonal AC. 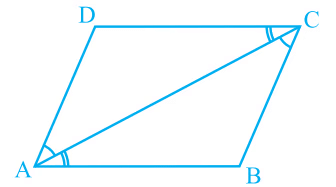 Diagonal AC divides the parallelogram into triangles ∆ABC and ∆CDA.
Diagonal AC divides the parallelogram into triangles ∆ABC and ∆CDA.
In ∆ ABC and ∆ CDA
∠BCA = ∠DAC ------(alternate interior angles)
∠BAC = ∠DCA ------(alternate interior angles)
Also, AC = AC------(common side).
Therefore, by the ASA rule,
∆ABC ≅ ∆CDA
Therefore, diagonal AC divides the parallelogram into congruent triangles.
Hence proved
Theorem 2: In a parallelogram, opposite sides are equal.
Proof: Consider parallelogram ABCD with diagonal AC. Diagonal AC divides the parallelogram into triangles ∆ABC and ∆CDA.
In ∆ ABC and ∆ CDA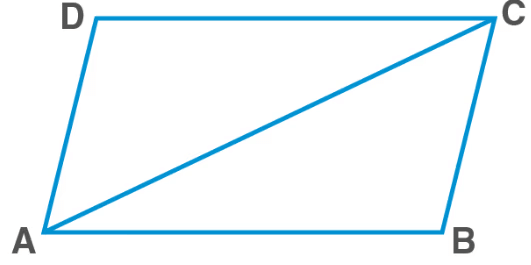
In ΔABC and ΔCDA
AC=AC (Common)
∠BCA=∠DAC (alternate angles)
∠BAC=∠DCA (alternate angles)
Therefore, by the ASA rule,
Δ ABC≅ΔCDA
Therefore, AB=DC and AD=BC (C.P.C.T.)
Hence proved
Theorem 3: If each pair of opposite sides of a quadrilateral is equal, then it is a parallelogram.

Given: ABCD is a quadrilateral where AD = CB and AB = CD.
To prove: ABCD is a parallelogram.
Construction: Join AC.
Proof:
In ΔABC and ΔCDA
AC=AC (Common)
∠BCA=∠DAC (alternate angles)
∠BAC=∠DCA (alternate angles)
Therefore, by the ASA rule,
Δ ABC≅ΔCDA
Therefore, by CPCT,
∠ACD =∠BAC
∠DAC =∠ACB
Since alternate angles are equal, thus the lines are parallel.
Therefore, AB∥CD and AD∥BC
Since both the pairs of opposite sides of the quadrilateral are parallel, ABCD is a parallelogram.
Hence proved.
Theorem 4: In a parallelogram, opposite angles are equal.
Proof: Consider parallelogram ABCD with diagonal AC. Diagonal AC divides the parallelogram into triangles ∆ABC and ∆CDA.
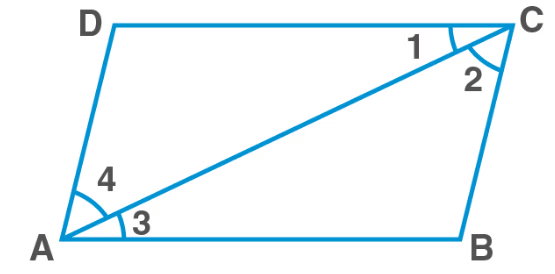
In parallelogram ABCD
AB‖CD; and AC is the transversal
Hence, ∠1=∠3….(1) (alternate interior angles)
BC‖DA; and AC is the transversal
Hence, ∠2 =∠4….(2) (alternate interior angles)
Adding (1) and (2)
∠1+∠2=∠3+∠4
∠BAD=∠BCD
Similarly,
∠ADC=∠ABC
Hence Proved.
Theorem 5: If in a quadrilateral, each pair of opposite angles is equal, then it is a parallelogram.
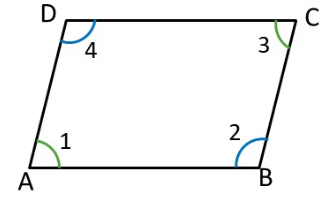
Given: ABCD is a quadrilateral with opposite angles equal,
i.e. , ∠1 = ∠3 and ∠2 = ∠4
To Prove: ABCD is a Parallelogram
Proof: By angle sum property of quadrilateral
∠1 + ∠2 + ∠3 + ∠4 = 360°
∠1 + ∠2 + ∠1 + ∠2 = 360° (Given ∠1 = ∠3 and ∠2 = ∠4)
2(∠1 + ∠2) = 360°
∠1 + ∠2 = 360° / 2
∠1 + ∠2 = 180° …(1)
Similarly, we can prove that,
∠1 + ∠4 = 180° …(2)
For lines AD and BC
with AB as transversal,
∠1 and ∠2 are interior angles on the same side of transversal, and
∠1 + ∠2 = 180°
Since interior angles on same side of transversal are supplementary,
Hence, AD || BC
For lines AB and DC
with AD as transversal,
∠1 and ∠4 are interior angles on the same side of transversal, and
∠1 + ∠4 = 180°
Since interior angles on same side of transversal are supplementary,
Hence, AB || DC
Thus, In ABCD,
Both pairs of opposite sides are parallel,
∴ ABCD is a parallelogram
 |
Download the notes
Proof of Theorems: Quadrilaterals
|
Download as PDF |
Theorem 6: The diagonals of a parallelogram bisect each other.
Proof: Draw diagonals AC and BD of parallelogram ABCD. Measure the lengths of OA, OB, OC, and OD. You will observe that OA = OC and OB = OD, or O is the midpoint of both diagonals. 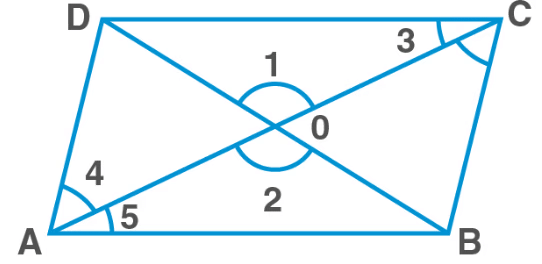
In Δ AOB and Δ COD,
∠3 =∠5 (alternate interior angles)
∠1 =∠2 (vertically opposite angles)
AB = CD (opp. Sides of parallelogram)
ΔAOB ≅ ΔCOD (AAS rule)
OB = OD and OA = OC (C.P.C.T)
Hence proved
If the diagonals of a quadrilateral bisect each other, then it is a parallelogram.
Theorem 7: If the diagonals of a quadrilateral bisect each other, then it is a parallelogram.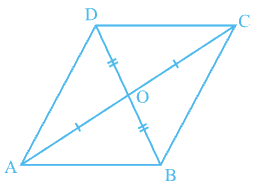
OD = OB (Given)
∠AOB = ∠COD (Vertically opposite angles are equal)
Therefore, ∆AOD ≅ ∆COB (By SAS criterion of congruence)
So, ∠OAD = ∠OCB ...(1) (C.P.C.T)
Now, lines AC intersect AD and BC at A and C respectively,
such that ∠OAD = ∠OCB …[from(1)]
∴ ∠OAD and ∠OCB form a pair of alternate interior angles are equal.
Thus, AD || BC
Similarly, we can prove that AB || DC
Hence, quadrilateral; ABCD is a parallelogram.
The Mid-point Theorem
In geometry, the Mid-point Theorem relates to the midpoints of the sides of a triangle. The theorem establishes a relationship between the line segment joining the midpoints of two sides of a triangle and the third side.
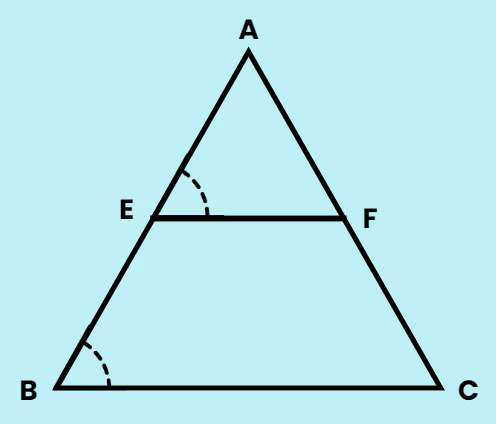
The Midpoint Theorem of a triangle states that if you connect the midpoints of two sides of a triangle with a line segment, that line segment will be parallel to the third side of the triangle, and its length will be half the length of the third side.
Let's explore this theorem and its converse.
Theorem 8: The line segment joining the mid-points of two sides of a triangle is parallel to the third side.
Activity Observation:
- Draw a triangle and mark mid-points E and F of two sides.
- Join E and F to form line segment EF.
- Measure EF and BC. You will observe that EF = 1/2 BC.
- Measure ∠AEF and ∠ABC. You will find that ∠AEF = ∠ABC.
- Therefore, EF is parallel to BC.
Proof: Consider triangle ABC with midpoints E and F of sides AB and AC, respectively. Draw CD parallel to BA. By the ASA rule, ∆AEF ≅ ∆CDF. This implies EF = DF and BE = AE = DC. Hence, BCDE is a parallelogram, leading to EF || BC.
Theorem 9: The line drawn through the mid-point of one side of a triangle, parallel to another side, bisects the third side.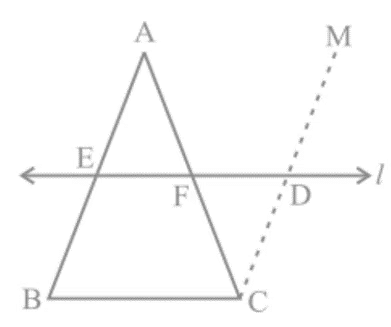
Proof: E is the mid-point of AB, and line l is parallel to BC with CM || BA. Prove AF = CF using the congruence of ∆AEF and ∆CDF.
Conclusion:
- The Mid-point Theorem and its converse provide a useful geometric relationship involving midpoints and parallel lines in triangles.
- These theorems are valuable tools for proving various properties and relationships within triangles.
|
40 videos|421 docs|51 tests
|






















