Best Study Material for Bank Exams Exam
Bank Exams Exam > Bank Exams Notes > Quantitative Aptitude/संख्यात्मक योग्यता > महत्वपूर्ण अवधारणाएँ: संख्या प्रणाली - 2
महत्वपूर्ण अवधारणाएँ: संख्या प्रणाली - 2 | Quantitative Aptitude/संख्यात्मक योग्यता - Bank Exams PDF Download
| Table of contents |
|
| इकाई अंक |
|
| चक्रीयता तालिका |
|
| शून्यों की संख्या |
|
| हल किये गए उदाहरण |
|
इकाई अंक
- इकाई अंक की अवधारणा को समझने के लिए, हमें चक्रीयता की अवधारणा को जानना होगा। यह अवधारणा मुख्य रूप से किसी संख्या के इकाई अंक और किसी निश्चित संख्या से विभाजित होने के उसके दोहराव वाले पैटर्न के बारे में है।
- इकाई अंक की अवधारणा को 0 से 9 तक की सभी एकल-अंकीय संख्याओं को कुछ निश्चित घातों तक बढ़ाने पर उनके इकाई अंक ज्ञात करके सीखा जा सकता है।
- इस उद्देश्य के लिए इन संख्याओं को मोटे तौर पर तीन श्रेणियों में वर्गीकृत किया जा सकता है:
1. अंक 0, 1, 5 और 6:
जब हम इन अंकों के व्यवहार का निरीक्षण करते हैं, तो पाते हैं कि इन सभी में इकाई का अंक वही होता है जो किसी भी घात पर बढ़ाए जाने पर स्वयं संख्या का होता है, अर्थात 0 n = 0, 1 n = 1, 5 n = 5, 6 n = 6।
5 2 = 25: इकाई अंक 5 है, जो कि संख्या ही है।
1 6 = 1: इकाई अंक 1 है, जो कि संख्या ही है।
0 4 = 0: इकाई अंक 0 है, जो कि संख्या ही है।
6 3 = 216: इकाई अंक 6 है, जो कि संख्या ही है।
आइए इस अवधारणा को निम्न उदाहरण पर लागू करें।
उदाहरण: निम्न संख्याओं का इकाई अंक ज्ञात करें:
- 185 563
उत्तर= 5 - 271 6987
उत्तर= 1 - 156 25369
उत्तर= 6 - 190 654789321
उत्तर= 0
2. अंक 4 और 9:
इन दोनों संख्याओं में केवल दो अलग-अलग अंकों की इकाई के रूप में चक्रीयता है ।
4 2 = 16: इकाई अंक 6 है।
4 3 = 64: इकाई अंक 4 है।
4 4 = 256: इकाई अंक 6 है।
4 5 = 1024: इकाई अंक 4 है।
9 2 = 81: इकाई अंक 1 है।
9 3 = 729: इकाई अंक 9 है।
यह देखा जा सकता है कि इकाई अंक 6 और 4 विषम-सम क्रम में दोहराए जा रहे हैं। इसलिए, 4 की चक्रीयता 2 है। 9 के साथ भी यही स्थिति है।
इसे निम्न प्रकार से सामान्यीकृत किया जा सकता है:
उदाहरण: निम्नलिखित संख्याओं का इकाई अंक ज्ञात कीजिए:
- 189 562589743
उत्तर = 9 (चूँकि घात विषम है) - 279 698745832
उत्तर = 1(चूँकि घात सम है) - 154 258741369
उत्तर = 4 (चूँकि घात विषम है) - 194 65478932
उत्तर = 6 (चूँकि घात सम है)
3. अंक 2, 3, 7 और 8:
इन संख्याओं में 4 अलग-अलग संख्याओं का घात चक्र होता है।
2 1 = 2 , 2 2 = 4 , 2 3 = 8 और 2 4 = 1 6 और उसके बाद यह दोहराना शुरू हो जाता है ।
तो, 2 की चक्रीयता में 4 अलग-अलग संख्याएँ 2, 4, 8, 6 हैं।
3 1 = 3 , 3 2 = 9 , 3 3 = 2 7 और 3 4 = 8 1 और उसके बाद यह दोहराना शुरू हो जाता है।
तो, 3 की चक्रीयता में 4 अलग-अलग संख्याएँ 3, 9, 7, 1 हैं।
7 और 8 समान तर्क का पालन करते हैं।
इसलिए इन चार अंकों यानी 2, 3, 7 और 8 में चार चरणों की एक इकाई अंक चक्रीयता है।
चक्रीयता तालिका
ऊपर चर्चा की गई अवधारणाओं का सारांश नीचे दी गई तालिका में दिया गया है।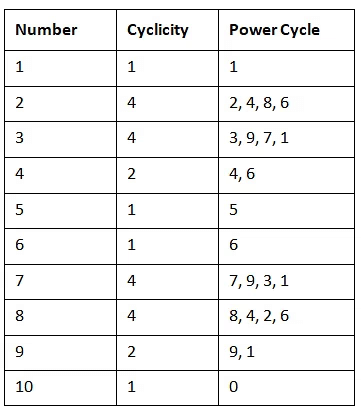
किसी संख्या की घात अवधारणा या चक्रीयता हमें किसी संख्या के अंतिम अंक का पता लगाने में मदद करती है, बिना वास्तव में पूरी संख्या की गणना किए। यह एक दोहराव पैटर्न पर आधारित है जो संख्या के अंतिम अंक पर निर्भर करता है। एक तालिका हमें इस अंतिम अंक का अनुमान लगाने में मदद करती है। साथ ही, एक या दो बार दिखाई देने वाले अंक हर चार बार दोहराए जाते हैं। इसलिए, प्रत्येक अंक हर चार बार दोहराया जाता है।
 |
परीक्षा: संख्या प्रणाली - 1
|
Start Test |
Start Test
शून्यों की संख्या
1. एक व्यंजक में शून्यों की संख्या
स्टेप 1
- मान लीजिए आपको किसी गुणनफल में शून्यों की संख्या ज्ञात करनी है: 24 × 32 × 17 × 23 × 19.
- हम सबसे पहले श्रृंखला को उसके अभाज्य गुणनखंडों अर्थात 2 3 ∗3 1 ∗2 5 ∗17 1 ∗19 ∗23 के रूप में प्राप्त करते हैं।
- जैसा कि आप देख सकते हैं, इस गुणनफल में कोई शून्य नहीं होगा क्योंकि इसमें 5 नहीं है।
- हालाँकि, यदि आपके पास कोई अभिव्यक्ति है: 8 × 15 × 23 × 17 × 25 × 22
- उपरोक्त अभिव्यक्ति को मानक रूप में पुनः लिखा जा सकता है: 2 3 ∗3 1 ∗5 1 ∗23∗17∗5 2 ∗2 1 ∗11 1
चरण दो
- शून्य 2 × 5 के संयोजन से बनते हैं।
- अतः शून्यों की संख्या 2 और 5 के बनने वाले जोड़ों की संख्या पर निर्भर करेगी।
- उपरोक्त गुणनफल में चार दो और तीन पाँच हैं। इसलिए, हम (2 × 5) के केवल तीन जोड़े ही बना पाएँगे।
- अतः गुणनफल में 3 शून्य होंगे।
2. फैक्टोरियल मान में शून्यों की संख्या ज्ञात करना
- विधि 1: मान लीजिए आपको 6! में शून्यों की संख्या ज्ञात करनी है । 6! = 6 × 5 × 4 × 3 × 2 × 1 = (3 × 2) × (5) × (2 × 2) × (3) × (2) × (1)।
5 की संख्या गिनने पर उत्तर मिल जाएगा। - विधि 2: 6! में शून्यों को खोजने के लिए हम का उपयोग करते हैं
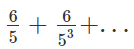इसलिए हमें उत्तर के रूप में 1 मिलता है क्योंकि श्रृंखला में पहले पद के बाद सभी भाग दशमलव में हैं जिन्हें हम अनदेखा करते हैं।
प्रश्न: 12 × 15 × 5 × 24 × 13 × 17
(ए) 0
(बी) 1
(सी) 2
(डी) 3
उत्तर: (सी)
हल: 2 2 ∗3∗3∗5∗5∗2 3 ∗3∗13∗17 = इसलिए (5*2) के जोड़े 2 हैं, इसलिए हमारे पास 2 शून्य हैं।
3. एक विशेष निहितार्थ
- 45!, 46!, 47!, 48!, 49! को हल करते समय ध्यान दें कि प्रत्येक स्थिति में शून्यों की संख्या 10 के बराबर होगी।
- यह समझना कठिन नहीं है कि इनमें से किसी भी फैक्टोरियल में पाँचों की संख्या 10 के बराबर है। शून्यों की संख्या केवल 50 पर ही बदलेगी! (यह 12 हो जाएगी)।
- वास्तव में, यह 5 के दो क्रमागत गुणनफलों के बीच सभी भाज्य मानों के लिए सत्य होगा।
- इस प्रकार, 50!, 51!, 52!, 53! और 54! में 12 शून्य होंगे (क्योंकि इन सभी में 12 पाँच हैं)। इसी तरह, 55!, 56!, 57!, 58! और 59! में से प्रत्येक में 13 शून्य होंगे।
- जबकि 49! में 10 शून्य हैं, 50! में सीधे 12 शून्य हैं। इसका मतलब है कि ऐसे किसी फैक्टोरियल का कोई मूल्य नहीं है जो 11 शून्य देगा। ऐसा इसलिए होता है क्योंकि 50! पाने के लिए हम 49! के मान को 50 से गुणा करते हैं। जब आप ऐसा करते हैं, तो परिणाम यह होता है कि हम गुणनफल में दो 5 जोड़ते हैं। इसलिए, शून्यों की संख्या दो से बढ़ जाती है।
- नोट: 124! पर आपको 24 + 4 = 28 शून्य मिलेंगे। 125! पर आपको 25 + 5 + 1 = 31 शून्य मिलेंगे। (3 शून्य की छलांग।)
उदाहरण: n! में 13 शून्य हैं। n के उच्चतम और न्यूनतम मान क्या हैं?
(ए) 57 और 58
(बी) 59 और 55
(सी) 59 और 6
(डी) 79 और 55
उत्तर: (बी)
हल: 55 पर हमें 13 शून्य मिलते हैं, क्योंकि हम जानते हैं कि 50! 12 शून्य हैं इसलिए 54! तक हमारे पास 12 शून्य होंगे। इसलिए 55 से 59! तक 13 शून्य होंगे।
हल किये गए उदाहरण
Q1: 5555 का अंतिम अंक ज्ञात करें 2345 + 6666 5678
(ए) 1
(बी) 3
(सी) 5
(डी) 7
उत्तर: (ए)
हल: चूंकि अंतिम अंक केवल अंतिम अंकों पर निर्भर करता है, इसलिए केवल अंतिम अंकों के लिए शक्तियों पर विचार करें, अर्थात 5 2345 + 6 5678। जैसा
कि हम जानते हैं, 5 की कोई भी शक्ति केवल 5 पर समाप्त होती है और 6 की कोई भी शक्ति केवल 6 पर समाप्त होती है।
52345 + 65678 का अंतिम अंक = 5 + 6 = 11 = 1
इसलिए, विकल्प (A) सही उत्तर है।
प्रश्न 2: यदि दो अंकों की संख्या में इकाई के स्थान का अंक z और दहाई के स्थान का अंक 8 है, तो संख्या है
(ए) 80z + z
(बी) 80 + z
(सी) 8z + 8
(डी) 80z + 1
उत्तर: (बी)
हल: इकाई के स्थान का अंक = z
दहाई के स्थान का अंक = 8
= 2-अंकीय संख्या = (10×8)+(1×z)
= 80 + z
प्रश्न 3: 60! में कितने अनुगामी शून्य (संख्या के अंत में शून्य) हैं?
(ए) 14
(बी) 12
(सी) 10
(डी) 8
उत्तर: (ए)
हल:
- सबसे पहले, किसी संख्या के दशमलव निरूपण में अंतिम शून्यों की संख्या = 10 की उच्चतम घात जो संख्या को विभाजित कर सकती है।
उदाहरण के लिए,
3600 = 36 * 102
45000 = 45 * 103 - इस प्रश्न का उत्तर देने के लिए, आइए सबसे पहले वह सबसे छोटा फैक्टोरियल देखें जो शून्य पर समाप्त होता है।
1! = 1
2! = 2
3! = 6
4! = 24
5! = 120
अब, 5! शून्य पर समाप्त होता है क्योंकि 1 * 2 * 3 * 4 * 5 की गणना करने पर हमें 10 का गुणनफल प्राप्त होता है।
10 = 2 * 5, इसलिए जब भी फैक्टोरियल में 2 और 5 आता है, हमें 10 का एक फैक्टर मिलता है।
तो, 5! में 1 शून्य है। 2 शून्य पर समाप्त होने वाला फैक्टोरियल 10 है!
15! में 3 शून्य हैं।
20! में 4 शून्य हैं और इसी तरह आगे भी।
2 और 5 के मिलने पर हर बार एक अतिरिक्त शून्य बनता है। प्रत्येक सम संख्या दो देती है, जबकि प्रत्येक पांचवीं संख्या हमें 5 देती है। - अब, यहाँ महत्वपूर्ण बात यह है कि चूँकि प्रत्येक सम संख्या फैक्टोरियल में कम से कम 2 का योगदान करती है, इसलिए 2 5 की तुलना में अधिक बार आता है। इसलिए, 10 की वह उच्चतम शक्ति ज्ञात करने के लिए जो किसी संख्या को विभाजित कर सकती है, हमें 5 की वह उच्चतम शक्ति गिननी होगी जो उस संख्या को विभाजित कर सकती है। हमें सिस्टम में 2 की संख्या गिनने की आवश्यकता नहीं है क्योंकि किसी भी फैक्टोरियल में 5 की तुलना में 2 अधिक होंगे।
- अब, 5 का हर गुणक फैक्टोरियल में एक शून्य जोड़ेगा। 1 * 2 * 3 *.......59 * 60 में 5 के बारह गुणक हैं। तो, ऐसा लगता है कि 60! 12 शून्यों पर समाप्त होगा। लेकिन हमें यहाँ एक और समायोजन करने की आवश्यकता है।
- 25 = 5 2 , इसलिए 25 अकेले दो 5 का योगदान देगा, और इसलिए सिस्टम में दो शून्य जोड़ देगा। इसी तरह, 25 का कोई भी गुणक एक अतिरिक्त शून्य का योगदान देगा।
- तो, 20! में 4 शून्य हैं, 25! में 6 शून्य हैं।
60! में [60/5] शून्य होंगे जो के गुणकों के कारण उत्पन्न होंगे और 25 और 50 की उपस्थिति के कारण एक अतिरिक्त [60/25] होगा।
{हम [60/25] के केवल पूर्णांक घटक को बनाए रखते हैं क्योंकि दशमलव भाग का कोई मान नहीं है} - अतः 60! का अंत 12 + 2 शून्य = 14 शून्य पर होगा।
- सामान्यतः, कोई भी n!
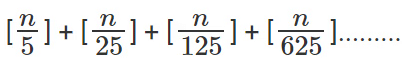शून्य पर समाप्त होगा। - आगे सामान्यीकरण करते हुए, यदि हम 3 की उच्चतम घात ज्ञात करना चाहते हैं जो n! को विभाजित करती है, तो यह कुछ और नहीं बल्कि है
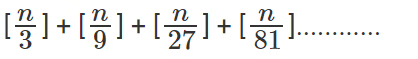
- 7 की वह उच्चतम घात जो n! को विभाजित करती है, है
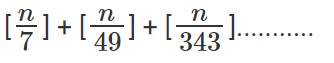
- किसी भाज्य संख्या के मामले में, हमें उसके अवयवी अभाज्य संख्याओं को तोड़ना होगा तथा संख्या को विभाजित करने वाली उच्चतम घात की गणना करनी होगी।
- उदाहरण के लिए, यदि हम 15 की सबसे बड़ी शक्ति ज्ञात करना चाहते हैं जो n! को विभाजित करती है, तो यह 3 और 5 की उच्चतम शक्तियों द्वारा संचालित होगी जो n! को विभाजित करती हैं। पिछले शून्यों के साथ हमने जो परिदृश्य देखा, उसके समान, हम देख सकते हैं कि किसी भी फैक्टोरियल में 5 की तुलना में कम से कम 3 अवश्य होंगे। इसलिए, 15 की उच्चतम शक्ति जो n! को विभाजित करती है, वह बस [n/5] + [n/25] + [n/125] + [n/625] है............
- अतः उत्तर "14" है
प्रश्न 4: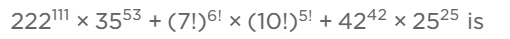 
(ए) 42
(बी) 53
(सी) 1055
(डी) इनमें से कोई नहीं के गुणनफल के अंत में शून्यों की संख्या
उत्तर: (ए)
हल: 222 111 × 35 53 के अंत में शून्यों की संख्या 53 है। (7!) 6! ×(10!) 5!
के अंत में शून्यों की संख्या 960 है। 42 42 ×25 25 के अंत में शून्यों की संख्या 42 है। इस प्रकार पूरे व्यंजक के अंत में शून्यों की संख्या 42 है।
The document महत्वपूर्ण अवधारणाएँ: संख्या प्रणाली - 2 | Quantitative Aptitude/संख्यात्मक योग्यता - Bank Exams is a part of the Bank Exams Course Quantitative Aptitude/संख्यात्मक योग्यता.
All you need of Bank Exams at this link: Bank Exams
|
223 docs|265 tests
|
FAQs on महत्वपूर्ण अवधारणाएँ: संख्या प्रणाली - 2 - Quantitative Aptitude/संख्यात्मक योग्यता - Bank Exams
| 1. इकाई अंक क्या होते हैं और इनका महत्व क्या है? |  |
| 2. चक्रीयता तालिका क्या है और इसे कैसे बनाया जाता है? | |
Ans. चक्रीयता तालिका एक गणितीय उपकरण है जो संख्याओं की पुनरावृत्ति को दर्शाता है। इसे बनाने के लिए, हम संख्याओं को एक निश्चित क्रम में व्यवस्थित करते हैं और देखते हैं कि कौन से अंक बार-बार आते हैं।
| 3. शून्यों की संख्या कैसे निर्धारित की जाती है? | |
Ans. शून्यों की संख्या किसी संख्या में शून्य के स्थानों की गणना करके निर्धारित की जाती है। उदाहरण के लिए, संख्या 1000 में तीन शून्य हैं। इसे पहचानने के लिए, हमें संख्या के अंतिम अंकों पर ध्यान देना चाहिए।
| 4. संख्या प्रणाली क्या होती है? | |
Ans. संख्या प्रणाली एक संरचना है जो संख्याओं को व्यवस्थित और वर्गीकृत करने के लिए उपयोग की जाती है। इसमें विभिन्न प्रकार की प्रणालियाँ होती हैं जैसे कि दशमलव, द्विआधारी, और अष्टाधारी। प्रत्येक प्रणाली के अपने नियम और विशेषताएँ होती हैं।
| 5. उदाहरणों का हल कैसे किया जाता है? | |
Ans. उदाहरणों का हल करने के लिए, पहले प्रश्न को समझना आवश्यक है। फिर, दिए गए डेटा का विश्लेषण करके, सही गणना और विधि का उपयोग करके उत्तर निकाला जाता है। यह प्रक्रिया अभ्यास के माध्यम से सुधारी जा सकती है।
Related Exams
About this Document
Mar 29, 2025
Last updated
Document Description: महत्वपूर्ण अवधारणाएँ: संख्या प्रणाली - 2 for Bank Exams 2025 is part of Quantitative Aptitude/संख्यात्मक योग्यता preparation.
The notes and questions for महत्वपूर्ण अवधारणाएँ: संख्या प्रणाली - 2 have been prepared according to the Bank Exams exam syllabus. Information about महत्वपूर्ण अवधारणाएँ: संख्या प्रणाली - 2 covers topics
like इकाई अंक, चक्रीयता तालिका, शून्यों की संख्या, हल किये गए उदाहरण and महत्वपूर्ण अवधारणाएँ: संख्या प्रणाली - 2 Example, for Bank Exams 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for महत्वपूर्ण अवधारणाएँ: संख्या प्रणाली - 2.
Introduction of महत्वपूर्ण अवधारणाएँ: संख्या प्रणाली - 2 in English is available as part of our Quantitative Aptitude/संख्यात्मक योग्यता
for Bank Exams & महत्वपूर्ण अवधारणाएँ: संख्या प्रणाली - 2 in Hindi for Quantitative Aptitude/संख्यात्मक योग्यता course.
Download more important topics related with notes, lectures and mock test series for Bank Exams
Exam by signing up for free. Bank Exams: महत्वपूर्ण अवधारणाएँ: संख्या प्रणाली - 2 | Quantitative Aptitude/संख्यात्मक योग्यता - Bank Exams
Description
Full syllabus notes, lecture & questions for महत्वपूर्ण अवधारणाएँ: संख्या प्रणाली - 2 | Quantitative Aptitude/संख्यात्मक योग्यता - Bank Exams - Bank Exams | Plus excerises question with solution to help you revise complete syllabus for Quantitative Aptitude/संख्यात्मक योग्यता | Best notes, free PDF download
Information about महत्वपूर्ण अवधारणाएँ: संख्या प्रणाली - 2
In this doc you can find the meaning of महत्वपूर्ण अवधारणाएँ: संख्या प्रणाली - 2 defined & explained in the simplest way possible. Besides explaining types of
महत्वपूर्ण अवधारणाएँ: संख्या प्रणाली - 2 theory, EduRev gives you an ample number of questions to practice महत्वपूर्ण अवधारणाएँ: संख्या प्रणाली - 2 tests, examples and also practice Bank Exams
tests
Related Searches
महत्वपूर्ण अवधारणाएँ: संख्या प्रणाली - 2 | Quantitative Aptitude/संख्यात्मक योग्यता - Bank Exams
,Free
,Extra Questions
,Important questions
,Viva Questions
,past year papers
,महत्वपूर्ण अवधारणाएँ: संख्या प्रणाली - 2 | Quantitative Aptitude/संख्यात्मक योग्यता - Bank Exams
,Exam
,Semester Notes
,Previous Year Questions with Solutions
,Summary
,mock tests for examination
,महत्वपूर्ण अवधारणाएँ: संख्या प्रणाली - 2 | Quantitative Aptitude/संख्यात्मक योग्यता - Bank Exams
,study material
,Objective type Questions
,shortcuts and tricks
,MCQs
,video lectures
,practice quizzes
,ppt
,Sample Paper
;
Additional Information about महत्वपूर्ण अवधारणाएँ: संख्या प्रणाली - 2 for Bank Exams Preparation
महत्वपूर्ण अवधारणाएँ: संख्या प्रणाली - 2 Free PDF Download
The महत्वपूर्ण अवधारणाएँ: संख्या प्रणाली - 2 is an invaluable resource that delves deep into the core of the Bank Exams exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the महत्वपूर्ण अवधारणाएँ: संख्या प्रणाली - 2 now and kickstart your journey towards success in the Bank Exams exam.
Importance of महत्वपूर्ण अवधारणाएँ: संख्या प्रणाली - 2
The importance of महत्वपूर्ण अवधारणाएँ: संख्या प्रणाली - 2 cannot be overstated, especially for Bank Exams aspirants.
This document holds the key to success in the Bank Exams exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
महत्वपूर्ण अवधारणाएँ: संख्या प्रणाली - 2 Notes
महत्वपूर्ण अवधारणाएँ: संख्या प्रणाली - 2 Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to महत्वपूर्ण अवधारणाएँ: संख्या प्रणाली - 2.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, महत्वपूर्ण अवधारणाएँ: संख्या प्रणाली - 2 Notes on EduRev are your ultimate resource for success.
महत्वपूर्ण अवधारणाएँ: संख्या प्रणाली - 2 Bank Exams Questions
The "महत्वपूर्ण अवधारणाएँ: संख्या प्रणाली - 2 Bank Exams Questions" guide is a valuable resource for all aspiring students preparing for the
Bank Exams exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study महत्वपूर्ण अवधारणाएँ: संख्या प्रणाली - 2 on the App
Students of Bank Exams can study महत्वपूर्ण अवधारणाएँ: संख्या प्रणाली - 2 alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the महत्वपूर्ण अवधारणाएँ: संख्या प्रणाली - 2,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of महत्वपूर्ण अवधारणाएँ: संख्या प्रणाली - 2 is prepared as per the latest Bank Exams syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily