परिचय: सीधी रेखा में गति | विज्ञान और प्रौद्योगिकी (Science & Technology) for UPSC CSE PDF Download

क्या आप जानते हैं कि ब्रह्मांड में सब कुछ हमेशा गतिमान रहता है? यहां तक कि जब आप अपने बिस्तर पर सो रहे होते हैं, तब भी आप पृथ्वी से जुड़े होते हैं, जो निरंतर अपने ध्रुव के चारों ओर और सूर्य के चारों ओर घूम रही है।

इसका अर्थ है कि आप भी गतिमान हैं। यह जानना आपके लिए दिलचस्प होगा कि इस ब्रह्मांड में कुछ भी पूरी तरह से स्थिर नहीं है। इसलिए, गति के बारे में समझना आपके लिए बहुत महत्वपूर्ण हो जाता है।

इस दस्तावेज़ में, हम गति और इसके पैरामीटर का विस्तार से अध्ययन करेंगे।

संदर्भ फ्रेम क्या है?

भौतिकी में, संदर्भ फ्रेम एक अमूर्त समन्वय प्रणाली और भौतिक संदर्भ बिंदुओं का सेट होता है जो समन्वय प्रणाली को अनोखे ढंग से फिक्स करता है और उस फ्रेम के भीतर माप को मानकीकृत करता है। आइए निम्नलिखित चित्र पर विचार करें:

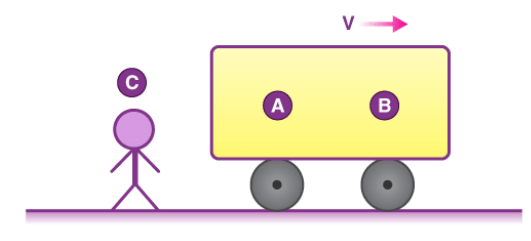
यदि हम A से पूछें कि B की गति क्या है, तो वह कहेगा कि यह स्थिर है। लेकिन यदि हम C से वही प्रश्न पूछते हैं, तो वह कहेगा कि B सकारात्मक X दिशा में गति V के साथ चल रहा है। तो हम देख सकते हैं कि गति को निर्दिष्ट करने से पहले हमें यह बताना होगा कि हम किस फ्रेम में हैं या सरल शब्दों में, हमें एक संदर्भ फ्रेम को परिभाषित करना होगा।

संदर्भ फ्रेम के प्रकार

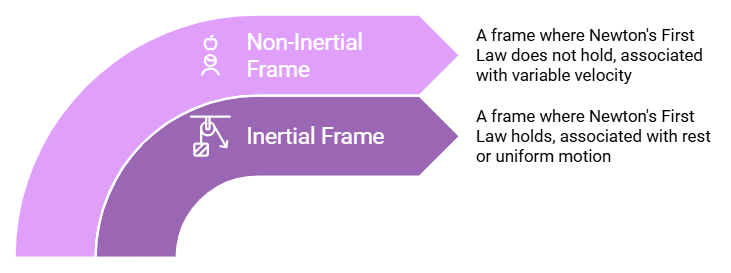
• जड़ता संदर्भ फ्रेम: यह वह फ्रेम है जिसमें न्यूटन का पहला गति का नियम लागू होता है। इसका अर्थ है कि यह एक ऐसे व्यक्ति से जुड़ा हुआ फ्रेम है जो स्थिर है या समान गति में है।
• गैर-जड़ता संदर्भ फ्रेम: यह वह संदर्भ फ्रेम है जिसमें न्यूटन का पहला गति का नियम लागू नहीं होता है। इसका अर्थ है कि यह एक ऐसे व्यक्ति से जुड़ा हुआ फ्रेम है जो परिवर्तनीय गति के साथ चल रहा है।

फ्रेम ऑफ रेफरेंस के प्रकार

पॉइंट मास ऑब्जेक्ट

आम तौर पर, भौतिकी में, एक वस्तु को एक पॉइंट मास ऑब्जेक्ट के रूप में माना जा सकता है, अर्थात इसकी गति में यात्रा की गई दूरी इसके आयामों के मुकाबले बहुत बड़ी होती है। पॉइंट मास ऑब्जेक्ट का उदाहरण:

पृथ्वी के चारों ओर परिक्रमा करने वाला एक उपग्रह एक पॉइंट मास ऑब्जेक्ट है।

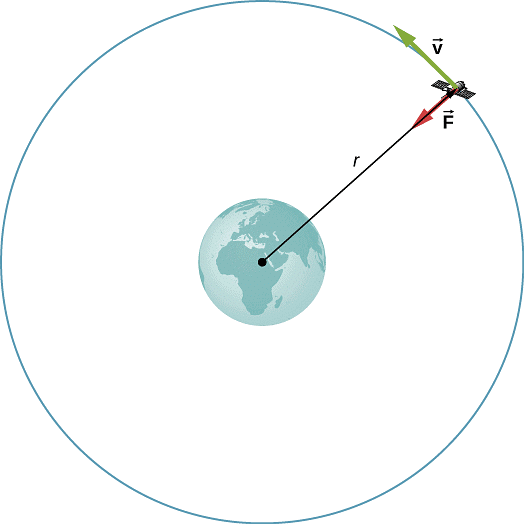
• पॉइंट-मास ऑब्जेक्ट का एक उदाहरण पृथ्वी के चारों ओर परिक्रमा करने वाला उपग्रह है। यद्यपि उपग्रहों के भौतिक आयाम होते हैं, उनकी गति को प्रभावी रूप से एक पॉइंट मास के रूप में माना जा सकता है। उपग्रह का आकार और आकृति अंतरिक्ष में यात्रा की गई विशाल दूरी की तुलना में महत्वहीन है।
• उपग्रह को एक पॉइंट मास के रूप में मानकर, हम इसकी पथ, कक्षीय गति और अन्य खगोलीय पिंडों के साथ गुरुत्वीय इंटरैक्शन का निर्धारण करने में शामिल गणनाओं को सरल बना सकते हैं। यह अनुमान उपग्रह की गति के विश्लेषण और भविष्यवाणी को अधिक सरल बनाता है।

गति और विश्राम

• गति: गति उस स्थिति को संदर्भित करती है जब एक वस्तु एक संदर्भ बिंदु या फ्रेम ऑफ रेफरेंस के सापेक्ष अपनी स्थिति बदल रही होती है। गति में वस्तुएँ विभिन्न विशेषताओं को प्रदर्शित कर सकती हैं, जिसमें गति, दिशा और त्वरण शामिल हैं।

• विश्राम: दूसरी ओर, विश्राम उस स्थिति का वर्णन करता है जब एक वस्तु संदर्भ बिंदु या फ्रेम ऑफ रेफरेंस के सापेक्ष अपनी स्थिति नहीं बदल रही है। विश्राम में एक वस्तु की स्थिति स्थिर होती है और वह नहीं चलती। अन्य शब्दों में, इसकी गति शून्य होती है, और यह अपने चारों ओर के सापेक्ष स्थिर रहती है।
• विश्राम और गति सापेक्ष शब्द हैं। एक वस्तु एक फ्रेम ऑफ रेफरेंस में विश्राम में दिखाई दे सकती है लेकिन दूसरे में गति में हो सकती है। यह निर्भर करता है कि पर्यवेक्षक का फ्रेम ऑफ रेफरेंस क्या है। दूसरे शब्दों में, विश्राम की कोई भी निरपेक्ष स्थिति या गति की कोई निरपेक्ष स्थिति नहीं होती; यह इस पर निर्भर करता है कि आप वस्तु को कैसे देख रहे हैं। उदाहरण के लिए, एक व्यक्ति जो अपने घर में बैठा है, वह पृथ्वी के सापेक्ष विश्राम में है लेकिन चंद्रमा के सापेक्ष गति में है।

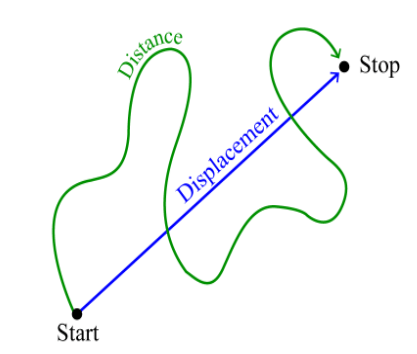
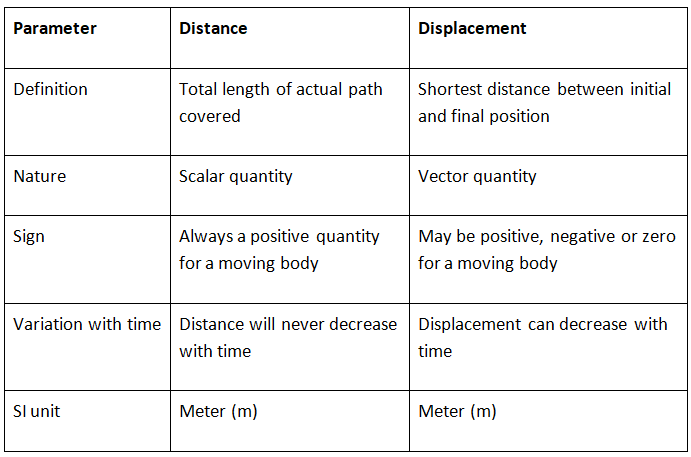
दूरी और विस्थापन

महत्वपूर्ण

• यदि एक कण सीधी रेखा में बिना दिशा बदले चल रहा है, तो विस्थापन की मात्रा यात्रा की गई दूरी के बराबर होती है, अन्यथा, विस्थापन हमेशा दूरी से कम होता है। इसलिए, विस्थापन और दूरी का संख्यात्मक अनुपात हमेशा एक से कम या बराबर होता है।
• यदि प्रारंभिक बिंदु और गति का अंतिम बिंदु समान हैं, तो विस्थापन का मान हमेशा शून्य होता है।

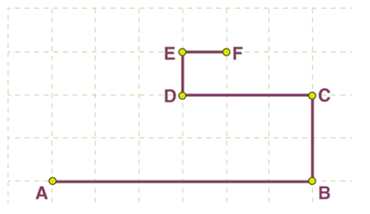
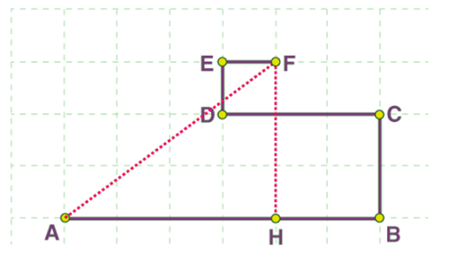
उदाहरण 1: एक वस्तु नीचे दिखाए गए A, B, C, D, E, और F बिंदुओं के माध्यम से ग्रिड पर चलती है। चौकोर टाइल्स की भुजा 0.5 किमी मापती है।

• (क) चलने वाली वस्तु द्वारा तय की गई दूरी की गणना करें।
• (ख) वस्तु के विस्थापन की मात्रा ज्ञात करें।

हल:

• (क) चलने वाली वस्तु द्वारा तय की गई दूरी कुल पथ की लंबाई है: AB + BC + CD + DE + EF = 3 + 1 + 1.5 + 0.5 + 0.5 = 6.5 किमी।
• चलने वाली वस्तु द्वारा तय की गई दूरी 6.5 किमी है।
• (ख) विस्थापन AF के बराबर है, जो प्रारंभिक और अंतिम स्थिति के बीच की सबसे छोटी दूरी है।
• पाइथागोरस सूत्र का उपयोग करते हुए, हमें मिलता है, (AF)² = (AH)² + (HF)² = (4 x 0.5)² + (3 x 0.5)² = (2)² + (1.5)² = 4 + 2.25 = 6.25 किमी।
• AF = 2.5 किमी।

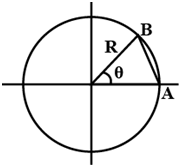
उदाहरण 2: एक कण A से B तक एक वृत्ताकार पथ में रेडियस R पर θ कोण को कवर करते हुए चल रहा है, जैसा कि चित्र में दिखाया गया है। कण की दूरी और विस्थापन की मात्रा का अनुपात ज्ञात करें।

• उत्तर: कण द्वारा तय की गई दूरी AB का आर्क लंबाई है।
• आर्क लंबाई = रेडियस x θ = Rθ।
• विस्थापन = AB।
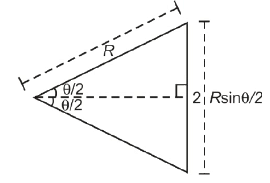
• यदि हम वृत्त के केंद्र से AB पर एक लंबवत बिसेक्टर गिराते हैं, तो हमें चित्र में दिखाए अनुसार मिलता है।
• उपरोक्त चित्र से हम निष्कर्ष निकाल सकते हैं कि, विस्थापन = AB = 2Rsin(θ/2)।

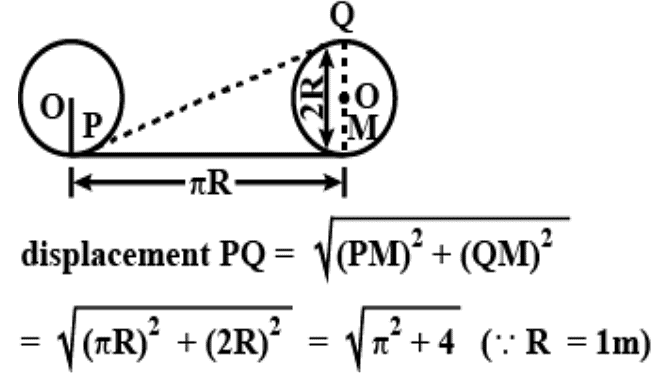
उदाहरण 3: एक पहिया जिसका त्रिज्या 1 मीटर है, समतल जमीन पर आधी क्रांति करता है। पहिये का वह बिंदु जो प्रारंभ में जमीन के संपर्क में था, उसकी विस्थापन की मात्रा क्या होगी? समाधान:

गति और वेग

किसी वस्तु की स्थिति में किसी भी दिशा में परिवर्तन की समय दर को वस्तु की गति कहा जाता है।

• S.I. इकाई m/s है। यह एक स्केलर मात्रा है। इसका आयामी सूत्र [M⁰L¹T^-1] है।

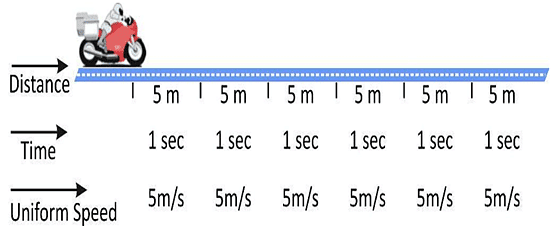
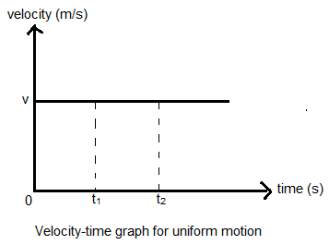
(a) समान गति

यदि कोई वस्तु समान समयांतराल में समान दूरी तय करती है, तो उसकी गति को समान गति कहा जाता है। ऐसी गति को समान गति कहा जाता है।

उदाहरण 4: मान लीजिए एक कार 4 घंटे में 300 किलोमीटर की दूरी तय करती है। कार की गति की गणना करें। समाधान: इस मामले में, तय की गई दूरी 300 किलोमीटर है, और समय 4 घंटे है। इन मानों को सूत्र में डालते हैं, हमें मिलता है:

गति = 300 किमी / 4 घंटे

गणना को सरल करते हुए, हम पाते हैं: गति = 75 किमी/घंटा। इस प्रकार, कार की समान गति 75 किलोमीटर प्रति घंटे है। इसका अर्थ है कि कार हर यात्रा समय के लिए 75 किलोमीटर की एक समान दर से यात्रा कर रही है।

(b) औसत गति

किसी वस्तु द्वारा तय की गई कुल दूरी और लिए गए कुल समय का अनुपात औसत गति कहा जाता है।

• यदि एक कण दूरी s₁, s₂, s₃, ... तय करता है और उसकी गति v₁, v₂, v₃, ... है, तो,
• यदि कण समान दूरी (s₁ = s₂ = s) तय करता है और उसकी गति v₁ और v₂ है, तो, औसत गति = (v₁ + v₂) / 2
• यदि एक कण गति v₁, v₂, v₃, ... के साथ समयांतराल t₁, t₂, t₃, ... में यात्रा करता है, तो,
• औसत गति = (v₁t₁ + v₂t₂ + v₃t₃ ...) / (t₁ + t₂ + t₃ ...)
• यदि कण गति v₁ और v₂ के साथ समान समयांतराल के लिए यात्रा करता है, अर्थात् t₁ = t₂ = t₃, तो,
• औसत गति = (v₁ + v₂) / 2
• जब कोई वस्तु समान दूरी तय करती है गति v₁ और v₂ के साथ, तो औसत गति (v) दोनों गति का हार्मोनिक माध्य होती है, 2/v = 1/v₁ + 1/v₂

उदाहरण 5: मान लीजिए एक कार 60 किमी की दूरी 40 किमी/घंटा की गति से तय करती है और फिर उसी दूरी 60 किमी को 60 किमी/घंटा की गति से तय करती है। कार की औसत गति क्या होगी? समाधान: कार की औसत गति निकालने के लिए, हम सूत्र का उपयोग करते हैं:

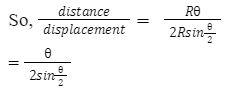
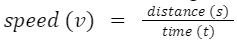
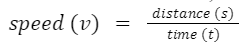
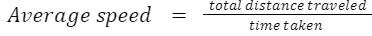
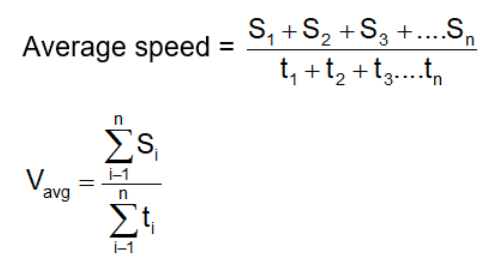
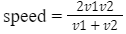
गाड़ी द्वारा तय की गई कुल दूरी है:

कुल दूरी = 60 किमी + 60 किमी = 120 किमी।

• पहले खंड के लिए समय (60 किमी, 40 किमी/घंटा): t1 = दूरी/गति = 60/40 = 1.5 घंटे।
• दूसरे खंड के लिए समय (60 किमी, 60 किमी/घंटा): t2 = दूरी/गति = 60/60 = 1 घंटा।

कुल समय = t1 + t2 = 1.5 + 1 = 2.5 घंटे।

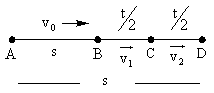
उदाहरण 6: एक कण सीधी रेखा में यात्रा करते हुए दूरी का आधा भाग गति V0 से चलता है। शेष दूरी का भाग गति V1 से आधे समय के लिए और गति V2 से दूसरे आधे समय के लिए तय किया जाता है। पूरे आंदोलन के समय में कण की औसत गति है। समाधान: दिया गया है कि कण ने यात्रा A से D तक की = 2s। इसने A से B तक की दूरी तय की = s गति = v0। समय लिया गया। इसने B से D तक की दूरी तय की = 2s समय = t। इस प्रकार हमें मिलता है BD = BC + CD.

उदाहरण 7: एक आदमी अपने घर से 2.5 किमी दूर एक बाजार की ओर सीधी सड़क पर 5 किमी/घंटा की गति से चलता है। बाजार बंद देखकर, वह तुरंत मुड़ता है और 7.5 किमी/घंटा की गति से घर वापस लौटता है। यदि यात्रा का कुल समय 40 मिनट है, तो पूरे यात्रा के लिए आदमी की औसत गति ज्ञात करें। समाधान: दिए गए डेटा:

• घर और बाजार के बीच की दूरी = 2.5 किमी
• यात्रा का कुल समय = 40 मिनट
• गति = 5 किमी/घंटा और 7.5 किमी/घंटा

औसत गति ज्ञात करने के लिए: घर से बाजार जाने में समय लगता है समय = d/v = 2.5/5 = 1/2 घंटा = 30 मिनट। वह शेष समय, यानी 10 मिनट में 7.5 किमी/घंटा की गति से लौटता है। (40 मिनट यात्रा का कुल समय है और 30 मिनट बाजार जाने में समय लिया गया, इसलिए शेष समय 10 मिनट है।) दूरी = 7.5 × 10/60 = 1.25 किमी। औसत गति = कुल दूरी/कुल समय।

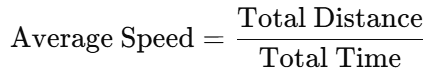
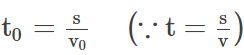
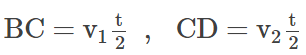
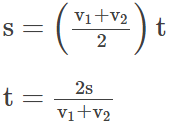
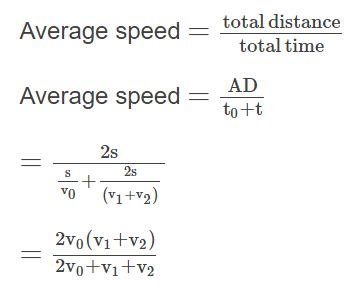
दूरी निम्नलिखित रूप में दी गई है:

2.5 किमी 1.25 किमी = 3.75 किमी
2.5 \\, \\text{किमी} 1.25 \\, \\text{किमी} = 3.75 \\, \\text{किमी}

समय निम्नलिखित रूप में दिया गया है: 4060 घंटे \\frac{40}{60} \\, \\text{घंटे}, जो कि समकक्ष है:

4060 = 23 घंटे \\frac{40}{60} = \\frac{2}{3} \\, \\text{घंटे}

औसत गति की गणना करें:

गति = कुल दूरी / कुल समय
दूरी समय = 3.75 किमी / 23 घंटे = 3.75 × 32 = 458 किमी/घंटा = 5.625 किमी/घंटा

इस प्रकार औसत गति 5.625 किमी/घंटा है।

(c) गैर-समरूप या परिवर्तनशील गति

यदि कोई वस्तु समान समय अंतराल में असमान दूरी तय करती है, तो उसकी गति को गैर-समरूप या परिवर्तनशील गति कहा जाता है। ऐसी गति को गैर-समरूप गति कहा जाता है। नीचे दिखाए गए डेटा में, शरीर द्वारा तय की गई दूरी समान समय अंतराल में असमान है।

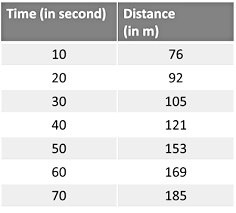
उदाहरण 8: मान लीजिए कि एक कार घुमावदार ट्रैक पर चल रही है। कार विश्राम से शुरू होती है और 100 मीटर की दूरी पर 20 मीटर/सेकंड की गति तक समान रूप से बढ़ती है। इस गति तक पहुँचने के बाद, यह समान रूप से अपनी गति कम करती है और 50 मीटर की दूरी पर रुक जाती है। इस पूरी गति के दौरान कार की औसत गति ज्ञात करें।

हल: इस पूरी गति के दौरान कार की औसत गति ज्ञात करने के लिए, हम सूत्र का उपयोग कर सकते हैं: औसत गति = कुल दूरी / कुल समय। सबसे पहले, हम त्वरण चरण के लिए लिए गए समय की गणना करते हैं:

गति का समीकरण का उपयोग करते हुए:
v² = u² + 2as, जहाँ v अंतिम वेग है, u आरंभिक वेग है, a त्वरण है, और s दूरी है। (हम इस दस्तावेज़ में बाद में गति के समीकरण पर चर्चा करेंगे)
20² = 0² + 2a(100)
400 = 200a
a = 400/200
a = 2 मीटर/सेकंड²

त्वरण चरण के लिए लिया गया समय इस समीकरण का उपयोग करके ज्ञात किया जा सकता है:

v = u + at, जहाँ v अंतिम वेग है, u प्रारंभिक वेग है, a त्वरण है, और t समय है।

20 = 0 + 2t

t = 20/2

t = 10 सेकंड

अब, हम मंदी के चरण के लिए लगे समय की गणना करते हैं: समान गति के समीकरण का उपयोग करते हुए:

v² = u² + 2as, जहाँ v अंतिम वेग है, u प्रारंभिक वेग है, a त्वरण है, और s दूरी है।

0 = 20² - 2a(50)

0 = 400 - 100a

100a = 400

a = 400/100

a = 4 m/s²

मंदी के चरण के लिए लगे समय की गणना की जा सकती है:

v = u + at, जहाँ v अंतिम वेग है, u प्रारंभिक वेग है, a त्वरण है, और t समय है।

0 = 20 - 4t

4t = 20

t = 20/4

t = 5 सेकंड

अब, हम गति के लिए कुल समय की गणना करते हैं:

कुल समय = त्वरण के लिए समय + मंदी के लिए समय

कुल समय = 10 सेकंड + 5 सेकंड

कुल समय = 15 सेकंड

अंत में, हम औसत गति की गणना कर सकते हैं:

औसत गति = कुल दूरी / कुल समय

कुल दूरी = त्वरण के दौरान दूरी + मंदी के दौरान दूरी

कुल दूरी = 100 मीटर + 50 मीटर

कुल दूरी = 150 मीटर

औसत गति = 150 मीटर / 15 सेकंड

औसत गति = 10 m/s

इसलिए, इस असमान गति के दौरान कार की औसत गति 10 m/s है।

किसी वस्तु के एक विशेष दिशा में विस्थापन में परिवर्तन की दर को उसका वेग कहा जाता है।

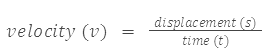
• इसका आयामिक सूत्र [M⁰ L¹T^-1] है।
• इसकी इकाई m/s है।
• यह एक वेक्टर गुण है, क्योंकि इसमें परिमाण और दिशा दोनों होते हैं।
• किसी वस्तु का वेग सकारात्मक, शून्य या नकारात्मक हो सकता है।

उदाहरण 9: मान लीजिए कि एक कार 150 किलोमीटर की दूरी 2 घंटे में तय करती है। कार का वेग ज्ञात करें।

हल: इस मामले में, विस्थापन 150 किलोमीटर है, और समय 2 घंटे है। इन मानों को सूत्र में डालते हैं:

वेग = 150 किमी / 2 घंटे = 75 किमी/घंटा।

इसलिए, कार का वेग 75 किलोमीटर प्रति घंटे है।

उदाहरण 10: एक कार बिंदु A से B तक 3 घंटे में यात्रा करती है और 5 घंटे में वापस बिंदु A पर लौटती है। बिंदु A और B के बीच की दूरी 150 मील है जो एक सीधी हाईवे पर है। कार की गति क्या है? समाधान: इस मामले में कार की गति शून्य है क्योंकि संवहन शून्य है (प्रारंभिक और अंतिम स्थिति समान हैं)।

(क) समान गति यदि कोई वस्तु समान समयांतराल में समान परिवर्तनों का अनुभव करती है, तो इसे समान गति से चलने वाला कहा जाता है।

महत्वपूर्ण: यह केवल तब संभव है जब एक वस्तु सीधी रेखा में बिना अपनी दिशा बदले यात्रा कर रही हो।

(ख) असमान या परिवर्तनशील गति यदि कोई वस्तु समान समयांतराल में असमान परिवर्तनों का अनुभव करती है, तो इसे असमान या परिवर्तनशील गति से चलने वाला कहा जाता है।

महत्वपूर्ण: यह केवल तभी संभव है जब वस्तु की गति का परिमाण या उसकी दिशा समय के सापेक्ष बदलती है।

(ग) औसत गति कुल परिवहन और कुल समय के अनुपात को औसत गति कहा जाता है।

उदाहरण 11: मान लें कि एक पर्वतारोही बिंदु A से शुरू होकर 2 घंटे में बिंदु B तक 10 किलोमीटर चलता है। बिंदु B पर एक छोटी सी विश्राम के बाद, पर्वतारोही बिंदु C तक पहुँचने के लिए 1.5 घंटे में और 6 किलोमीटर चलता है। पूरे यात्रा के लिए औसत गति ज्ञात करने के लिए, हम सूत्र का उपयोग कर सकते हैं: समाधान: औसत गति = कुल परिवहन / कुल समय। कुल परिवहन व्यक्तिगत परिवर्तनों का योग है, जो 10 किलोमीटर + 6 किलोमीटर = 16 किलोमीटर है। कुल समय व्यक्तिगत समय का योग है, जो 2 घंटे + 1.5 घंटे = 3.5 घंटे है। इन मानों को सूत्र में डालते हुए: औसत गति = 16 किमी / 3.5 घंटे ≈ 4.57 किमी/घंटा। इसलिए, पूरे यात्रा के लिए औसत गति लगभग 4.57 किलोमीटर प्रति घंटा है।

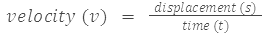
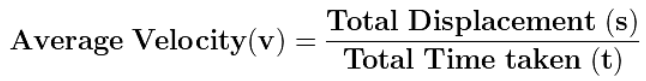
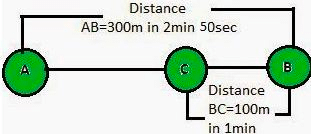
उदाहरण 12: जोसेफ एक सीधे 300 मीटर के रास्ते के एक सिरे A से दूसरे सिरे B तक 2 मिनट 50 सेकंड में दौड़ता है और फिर वापस लौटकर C बिंदु तक 100 मीटर दौड़ता है, जो कि अगले 1 मिनट में होता है। जोसेफ की औसत गति और वेग (a) A से B और (b) A से C के लिए क्या हैं? समाधान: (a) A से B तक कुल दूरी जो A से B तक तय की गई = 300 मीटर कुल विस्थापन = 300 मीटर कुल समय लिया गया = 2 × 60 सेकंड 50 सेकंड = 170 सेकंड इसलिए, A से B तक की औसत गति = कुल दूरी/कुल समय = 300/170 = 1.76 मीटर/सेकंड औसत वेग A से B तक = विस्थापन AB/समय = 1.76 मीटर/सेकंड (b) A से C तक कुल दूरी जो A से C तक तय की गई = AB + BC = 300 + 100 मीटर = 400 मीटर A से C तक का कुल समय = 170 सेकंड + 60 सेकंड = 230 सेकंड इसलिए, A से C तक की औसत गति = कुल दूरी/कुल समय = 400/230 = 1.74 मीटर/सेकंड A से C तक का विस्थापन = AC = AB - BC = 300 - 100 = 200 मीटर A से C तक के विस्थापन के लिए समय = 230 सेकंड इसलिए, A से C तक की औसत वेग = विस्थापन/समय = 200/230 मीटर/सेकंड = 0.87 मीटर/सेकंड

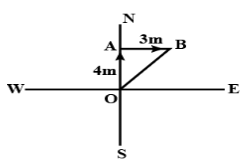
उदाहरण 13: एक कीड़ा 10 सेकंड में उत्तर दिशा में 4 मीटर की दूरी तय करता है और फिर 5 सेकंड में पूर्व दिशा में 3 मीटर की दूरी तय करता है। कीड़े की औसत वेग क्या है? समाधान:

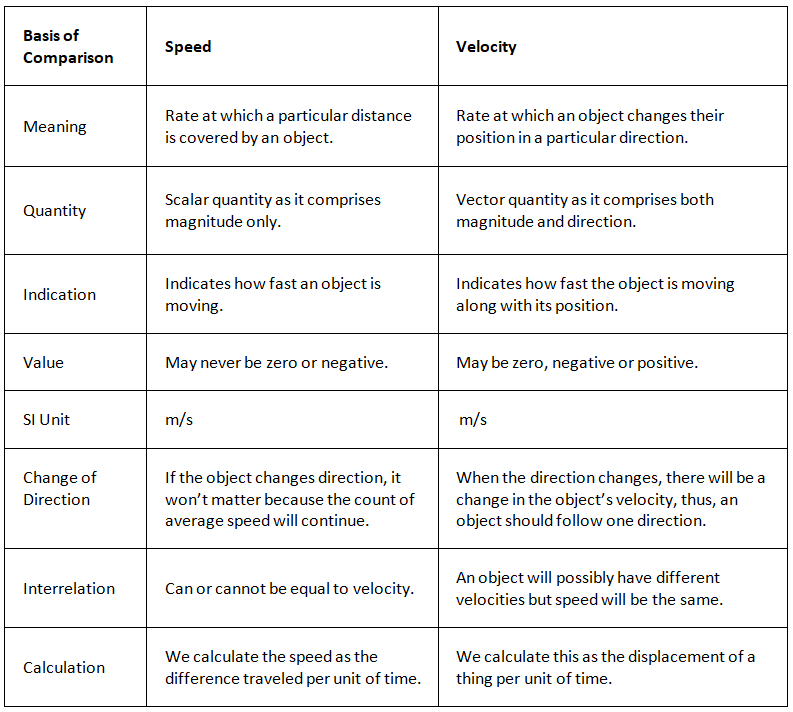
हम अक्सर गति और वेग के शब्दों का आपस में उपयोग करते हैं, जबकि यह जानना आवश्यक है कि ऐसा करना गलत है। गति और वेग के बीच एक अंतर है जिसे सभी को जानना चाहिए। नीचे इन दोनों शर्तों के बीच का अंतर दिया गया है।

त्वरण

वेग में परिवर्तन की समय दर को त्वरण कहा जाता है।

• इसकी इकाई m/s² है।
• इसका आयामी सूत्र [M₀L_T^-2] है।
• यह एक वेक्टर मात्रा है।

त्वरण सकारात्मक, शून्य या नकारात्मक हो सकता है। सकारात्मक त्वरण का अर्थ है कि समय के साथ वेग बढ़ता है, शून्य त्वरण का अर्थ है कि वेग समान है, जबकि नकारात्मक त्वरण (रिटार्डेशन) का अर्थ है कि समय के साथ वेग कम हो रहा है। यदि एक कण एक समय t₁ के लिए त्वरण a₁ के साथ और एक समय t₂ के लिए त्वरण a₂ के साथ त्वरण होता है। तब औसत त्वरण होगा: a_av = (a₁t₁ + a₂t₂) / (t₁ + t₂)

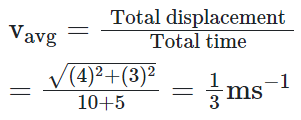
उदाहरण 14: मान लें कि एक कार जो प्रारंभ में विश्राम की स्थिति में है, समान रूप से त्वरित होती है और 6 सेकंड बाद 30 मीटर/सेकंड की अंतिम गति तक पहुँच जाती है। कार का औसत त्वरन ज्ञात करने के लिए, हम निम्नलिखित सूत्र का उपयोग कर सकते हैं:

समाधान: औसत त्वरन = (अंतिम गति - प्रारंभिक गति) / समय। इस मामले में, प्रारंभिक गति 0 मीटर/सेकंड है, अंतिम गति 30 मीटर/सेकंड है, और समय 6 सेकंड है। इन मानों को सूत्र में लगाने पर: औसत त्वरन = (30 मीटर/सेकंड - 0 मीटर/सेकंड) / 6 सेकंड = 5 मीटर/सेकंड²।

समान रूप से त्वरित गति

समान रूप से त्वरित गति उस वस्तु की गति को संदर्भित करती है जो एक स्थिर त्वरण का अनुभव कर रही है। इस प्रकार की गति में, वस्तु की गति समय के साथ एक स्थिर दर पर बदलती है।

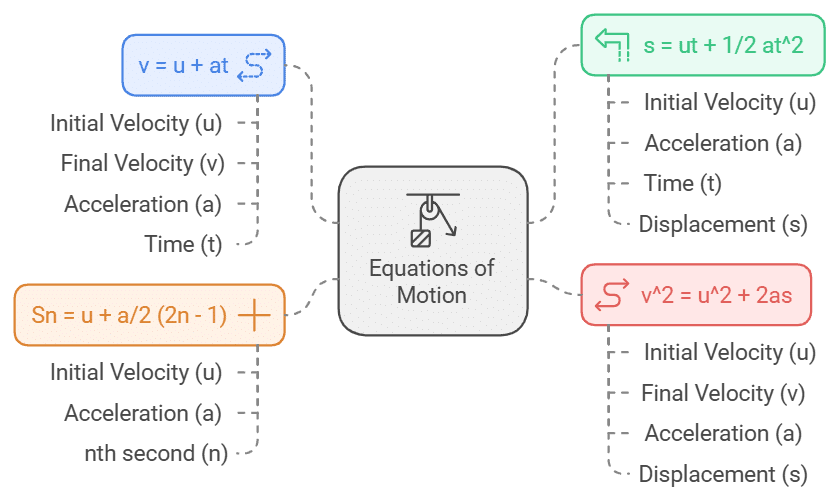
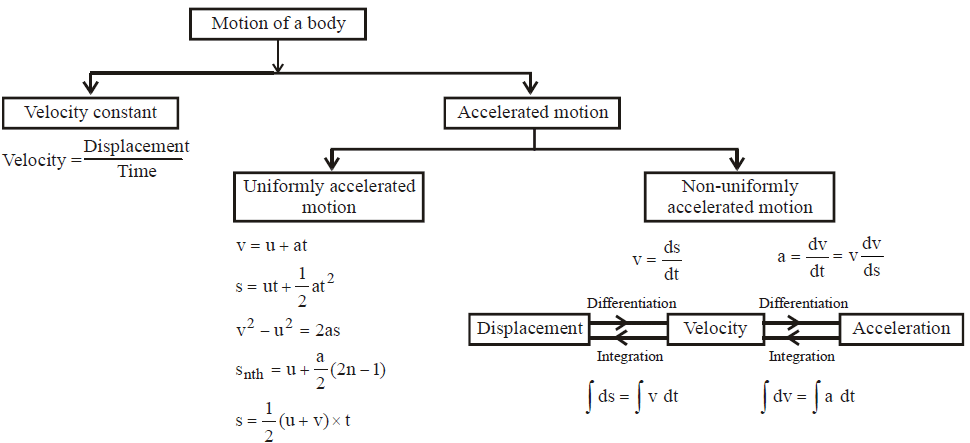
गति के समीकरण

यदि एक शरीर प्रारंभिक गति (u) के साथ शुरू होता है और समय t के बाद इसकी गति बदलकर v हो जाती है, यदि समान त्वरन a है और समय t में यात्रा की गई दूरी s है, तो निम्नलिखित संबंध प्राप्त होते हैं, जिन्हें समान रूप से त्वरित गति के समीकरण कहा जाता है।

(i) v = u + at

• v वस्तु की अंतिम गति का प्रतिनिधित्व करता है।
• u वस्तु की प्रारंभिक गति का प्रतिनिधित्व करता है।
• a वस्तु द्वारा अनुभव किए गए स्थिर त्वरन का प्रतिनिधित्व करता है।
• t वस्तु द्वारा त्वरन अनुभव करने में लगने वाले समय का प्रतिनिधित्व करता है।

(ii) s = ut + 1/2 at²

• s वस्तु द्वारा की गई विस्थापन या यात्रा की गई दूरी का प्रतिनिधित्व करता है।
• u वस्तु की प्रारंभिक गति का प्रतिनिधित्व करता है।
• a वस्तु द्वारा अनुभव किए गए स्थिर त्वरन का प्रतिनिधित्व करता है।
• t वस्तु द्वारा त्वरन अनुभव करने में लगने वाले समय का प्रतिनिधित्व करता है।

(iii) v² = u² + 2as

निम्नलिखित भौतिकी के कुछ समीकरणों का उपयोग करके वस्तुओं की गति और उनके वेलोसिटी (गति) में परिवर्तन को समझाया गया है।

• v वस्तु की अंतिम गति को दर्शाता है।
• u वस्तु की प्रारंभिक गति को दर्शाता है।
• a वस्तु द्वारा अनुभव की गई स्थिर त्वरण (acceleration) को दर्शाता है।
• s वस्तु द्वारा तय की गई दूरी या विस्थापन (displacement) को दर्शाता है।

(iv) nth सेकंड में तय की गई दूरी: Sn = u + (1/2) a (2n – 1)

• Sn nth सेकंड में तय की गई दूरी को दर्शाता है।
• u वस्तु की प्रारंभिक गति को दर्शाता है।
• a वस्तु द्वारा अनुभव की गई स्थिर त्वरण को दर्शाता है।
• n समय को सेकंड में दर्शाता है, विशेष रूप से गति के nth सेकंड को।

यदि कोई शरीर समान त्वरण के साथ गति करता है और उसकी गति u से v में समय अंतराल में बदलती है, तो उसके मार्ग के मध्य बिंदु पर गति क्या होगी। यहाँ कुछ संख्यात्मक उदाहरण दिए गए हैं:

(i) v = u + at: उदाहरण 15: मान लीजिए कि एक कार विश्राम से शुरू होती है (प्रारंभिक गति u = 0) और 5 सेकंड के लिए 2 m/s² की दर से त्वरण करती है। हम अंतिम गति (v) की गणना कर सकते हैं: v = u + at

v = 0 + (2 m/s²)(5 s) = 10 m/s इसलिए, 5 सेकंड के त्वरण के बाद कार की अंतिम गति 10 m/s है।

(ii) s = ut + (1/2) at^2: उदाहरण 16: मान लीजिए कि एक गेंद को 20 m/s की प्रारंभिक गति से ऊपर फेंका गया है। यदि हम 3 सेकंड बाद गेंद के विस्थापन (s) को ढूंढना चाहते हैं, तो हम समीकरण का उपयोग कर सकते हैं:

s = (20 m/s)(3 s) + (1/2)(-9.8 m/s²)(3 s)² ≈ 15 m इसलिए, गेंद का विस्थापन लगभग 15 मीटर है।

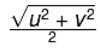
(iii) v² = u² + 2as: उदाहरण 16: मान लीजिए कि एक शरीर विश्राम से शुरू होता है (प्रारंभिक गति u = 0) और 4 m/s² की स्थिर त्वरण का अनुभव करता है। यदि हम 100 मीटर की दूरी तय करने के बाद अंतिम गति (v) को ढूंढना चाहते हैं, तो हम समीकरण का उपयोग कर सकते हैं:

v² = u² + 2as

v² = 0 + 2(4 m/s²)(100 m) = 800 m²/s² दोनों पक्षों का वर्गमूल लेते हुए, हमें मिलता है:

v ≈ 28.28 m/s इसलिए, 100 मीटर की दूरी तय करने के बाद शरीर की अंतिम गति लगभग 28.28 m/s है।

(iv) nth सेकंड में तय की गई दूरी Sn = u a/2(2n – 1): उदाहरण 17: मान लीजिए कि एक वस्तु की प्रारंभिक गति 10 m/s है और त्वरण 2 m/s² है। हम चौथे सेकंड में तय की गई दूरी ज्ञात करना चाहते हैं। हम सूत्र का उपयोग कर सकते हैं: Sn = u a / 2(2n – 1) S4 = 10 m/s (2 m/s²) / 2(2(4) – 1) S4 = 10 m/s 1 (7) S4 = 17 m इस प्रकार, चौथे सेकंड में तय की गई दूरी 17 मीटर है।

गुरुत्वाकर्षण के तहत गति

पृथ्वी द्वारा वस्तुओं पर लगाए जाने वाले आकर्षण बल को गुरुत्व बल कहा जाता है। गुरुत्व बल द्वारा वस्तु में उत्पन्न होने वाला त्वरण गुरुत्व त्वरण कहलाता है। इसे g के प्रतीक से दर्शाया जाता है। वायु प्रतिरोध के अभाव में, यह पाया गया है कि सभी वस्तुएं (आकार, वजन या संघटन की परवाह किए बिना) पृथ्वी की सतह के निकट समान त्वरण के साथ गिरती हैं। एक छोटी ऊँचाई (hमुक्त गिरावट कहा जाता है। (1) यदि कोई वस्तु किसी ऊँचाई से गिरती है, तो प्रारंभिक स्थिति को मूल बिंदु मानते हुए और गति की दिशा (यानि, नीचे की दिशा) को सकारात्मक मानते हैं, तो यहाँ हमारे पास:

यदि प्रारंभिक गति शून्य है, तो u = 0। समय के सापेक्ष दूरी, गति और त्वरण का ग्राफ:

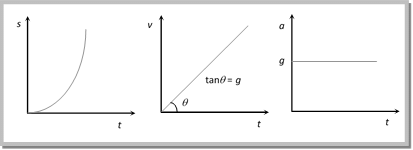
(3) यदि कोई वस्तु ऊर्ध्वाधर दिशा में प्रक्षिप्त की जाती है, प्रारंभिक स्थिति को मूल मानते हुए और गति की दिशा (यानि, ऊर्ध्वाधर ऊपर) को सकारात्मक मानते हुए, तो a = -g [क्योंकि त्वरण नीचे की ओर है जबकि गति ऊपर की ओर है]। इसलिए, यदि वस्तु को u गति के साथ प्रक्षिप्त किया जाता है और समय t के बाद यह ऊँचाई s तक पहुँचती है, तब समय के सापेक्ष दूरी, गति और त्वरण का ग्राफ (अधिकतम ऊँचाई के लिए): यह स्पष्ट है कि दोनों मात्राएँ वस्तु के द्रव्यमान पर निर्भर नहीं करती हैं या हम कह सकते हैं कि वायु प्रतिरोध के अभाव में, सभी वस्तुएं पृथ्वी की सतह पर समान गति से गिरती हैं। यहाँ ऊपर दिए गए समीकरणों के कुछ संख्यात्मक उदाहरण दिए गए हैं:

उदाहरण 18: गुरुत्वाकर्षण के तहत स्वतंत्र रूप से गिरने वाला वस्तु (u = 0):

• (i)v = u + gt: विचार करें कि एक वस्तु गुरुत्वाकर्षण के तहत स्वतंत्र रूप से गिर रही है, जिसकी त्वरित गति g = 9.8 m/s² है। यदि हम 3 सेकंड के स्वतंत्र गिरने के बाद अंतिम वेग (v) ज्ञात करना चाहते हैं, तो हम निम्नलिखित समीकरण का उपयोग कर सकते हैं:
  • v = u + gt
  • v = 0 + (9.8 m/s²)(3 s)
  • v = 29.4 m/s
• (ii)h = ut + 1/2gt²: स्वतंत्र गिरने के दौरान वस्तु द्वारा तय की गई ऊँचाई (h) ज्ञात करने के लिए, हम निम्नलिखित समीकरण का प्रयोग कर सकते हैं:
  • h = ut + 1/2gt²
  • h = 0 + 1/2(9.8 m/s²)(3 s)²
  • h = 44.1 m
• (iii)v² = u² + 2gh: स्वतंत्र रूप से गिरने वाली वस्तु के अंतिम वेग (v) का वर्ग ज्ञात करने के लिए समीकरण का उपयोग करते हुए:
  • v² = u² + 2gh
  • v² = 0² + 2(9.8 m/s²)(44.1 m)
  • v² = 862.68 m²/s²
  • v ≈ 29.38 m/s

उदाहरण 19: ऊपर फेंकी गई वस्तु: यदि एक वस्तु ऊपर की ओर फेंकी जाती है, तो गति के समीकरणों में गुरुत्वाकर्षण के कारण त्वरित गति (g) को (-g) से प्रतिस्थापित किया जाता है। आइए उदाहरण 1 के समान प्रारंभिक स्थितियों और समय मानों पर विचार करें:

• (i)v = u - gt: ऊपर फेंकी गई वस्तु के अंतिम वेग (v) के लिए समीकरण का उपयोग करते हुए:
  • v = u - gt
  • v = 0 - (9.8 m/s²)(3 s)
  • v = -29.4 m/s
• (ii)h = ut + 1/2(-g)t²: ऊपर फेंकी गई वस्तु द्वारा 3 सेकंड में पहुंची ऊँचाई (h) की गणना करने के लिए, हम समीकरण का उपयोग करते हैं:
  • h = ut + 1/2(-g)t²
  • h = 0 + 1/2(-9.8 m/s²)(3 s)²
  • h = -44.1 m (नोट: नकारात्मक चिह्न दर्शाता है कि वस्तु प्रारंभिक बिंदु से नीचे है।)
• (iii)v² = u² - 2gh: ऊपर फेंकी गई वस्तु के अंतिम वेग (v) के वर्ग के लिए समीकरण का उपयोग करते हुए:
  • v² = u² - 2gh
  • v² = 0² - 2(-9.8 m/s²)(-44.1 m)
  • v² = 862.68 m²/s²
  • v ≈ 29.38 m/s

ये उदाहरण दर्शाते हैं कि कैसे गति के समीकरणों का उपयोग स्वतंत्र रूप से गिरने वाले वस्तुओं और गुरुत्वाकर्षण के प्रभाव में ऊपर फेंकी गई वस्तुओं की गति का विश्लेषण करने के लिए किया जा सकता है।

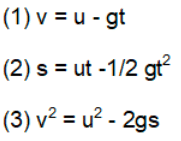
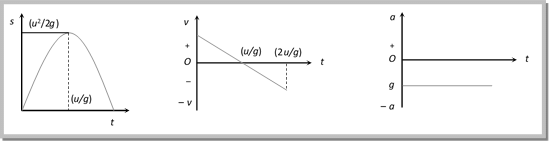
गैर-समान त्वरण गति

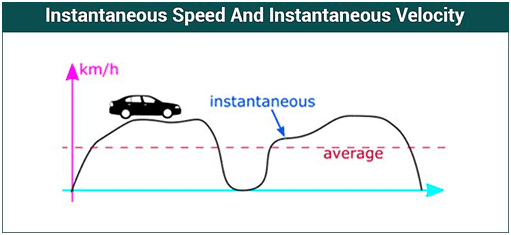
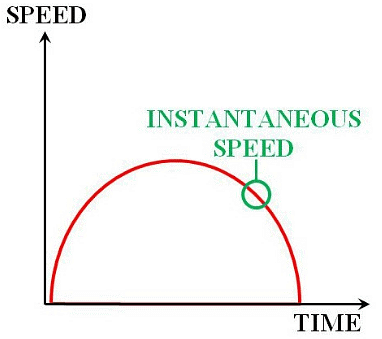
गैर-समान त्वरण गति उस वस्तु की गति को संदर्भित करती है जो अपनी गति को एक असमान दर पर बदल रही है। दूसरे शब्दों में, वस्तु त्वरण कर रही है या मंदी कर रही है, लेकिन त्वरण स्वयं समय के साथ स्थिर नहीं है। इस प्रकार की गति का विश्लेषण करना समान रूप से त्वरण गति की तुलना में अधिक जटिल हो सकता है, जहां त्वरण स्थिर रहता है। इस प्रकार की गति को समझने के लिए, किसी को तत्कालीन गति के बारे में जानना आवश्यक है। जब एक वस्तु परिवर्तनशील गति के साथ यात्रा कर रही होती है, तब किसी दिए गए क्षण में उसकी गति को उसकी तत्कालीन गति कहा जाता है।

उदाहरण 20: मान लीजिए कि एक कार एक सीधी सड़क पर यात्रा कर रही है, और इसकी स्थिति निम्नलिखित समीकरण द्वारा दी गई है: x(t) = 3t² - 2t + 1, जहाँ x समय t पर कार की स्थिति है। एक विशेष समय t पर कार की तत्कालीन गति ज्ञात कीजिए।

हल: एक विशेष समय t पर कार की तत्कालीन गति ज्ञात करने के लिए, हमें स्थिति फलन का समय के सापेक्ष व्युत्पत्ति (derivative) निकालनी होगी। व्युत्पत्ति हमें स्थिति के परिवर्तन की दर देगी, जो गति है। x(t) को t के सापेक्ष व्युत्पन्न करते हुए, हमें प्राप्त होता है:

अब, किसी विशेष समय पर तत्कालीन गति ज्ञात करने के लिए, गति फलन में t का मान प्रतिस्थापित करें। मान लीजिए हम t = 2 सेकंड पर तत्कालीन गति ज्ञात करना चाहते हैं:

v(2) = 6(2) - 2 = 12 - 2 = 10 m/s।

इसलिए, t = 2 सेकंड पर कार की तत्कालीन गति 10 m/s है।

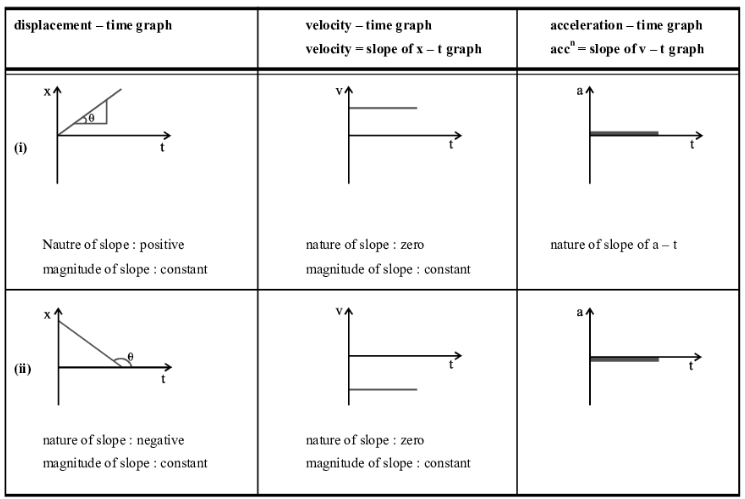
काइनेमेटिक्स से संबंधित ग्राफ

(i) समान गति (ii) गैर-समान गति

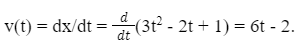
सापेक्ष गति (Relative Motion) 1-डी में

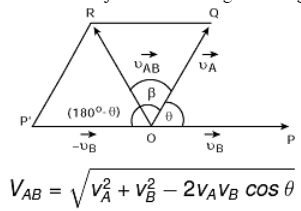
किसी एक वस्तु की सापेक्ष गति दूसरी वस्तु के सापेक्ष उस वस्तु की स्थिति में समय के साथ होने वाले परिवर्तन की दर है। वस्तु A की वस्तु B के सापेक्ष सापेक्ष गति को इस प्रकार व्यक्त किया जाता है: VAB = VA – VB

• जब दो वस्तुएं एक ही दिशा में चल रही होती हैं, तो VAB = VA - VB
• जब दो वस्तुएं विपरीत दिशा में चल रही होती हैं, तो VAB = VA + VB
• जब दो वस्तुएं कोण पर चल रही होती हैं, तो tan β = vB sin θ / (vA – vB cos θ)

उदाहरण 21: मान लीजिए कि दो कारें हैं, कार A और कार B, जो एक सीधी सड़क पर एक ही दिशा में चल रही हैं। कार A की गति 60 किमी/घंटा है, जबकि कार B की गति 80 किमी/घंटा है।

हल: कार B की कार A के सापेक्ष सापेक्ष गति ज्ञात करने के लिए, हम कार A की गति को कार B की गति से घटाते हैं।

कार B की कार A के सापेक्ष सापेक्ष गति = कार B की गति - कार A की गति

सापेक्ष गति = 80 किमी/घंटा - 60 किमी/घंटा = 20 किमी/घंटा। इसलिए, कार B की कार A के सापेक्ष सापेक्ष गति 20 किमी/घंटा है। इसका अर्थ है कि कार B कार A की तुलना में एक ही दिशा में 20 किमी/घंटा तेज चल रही है।

सारांश

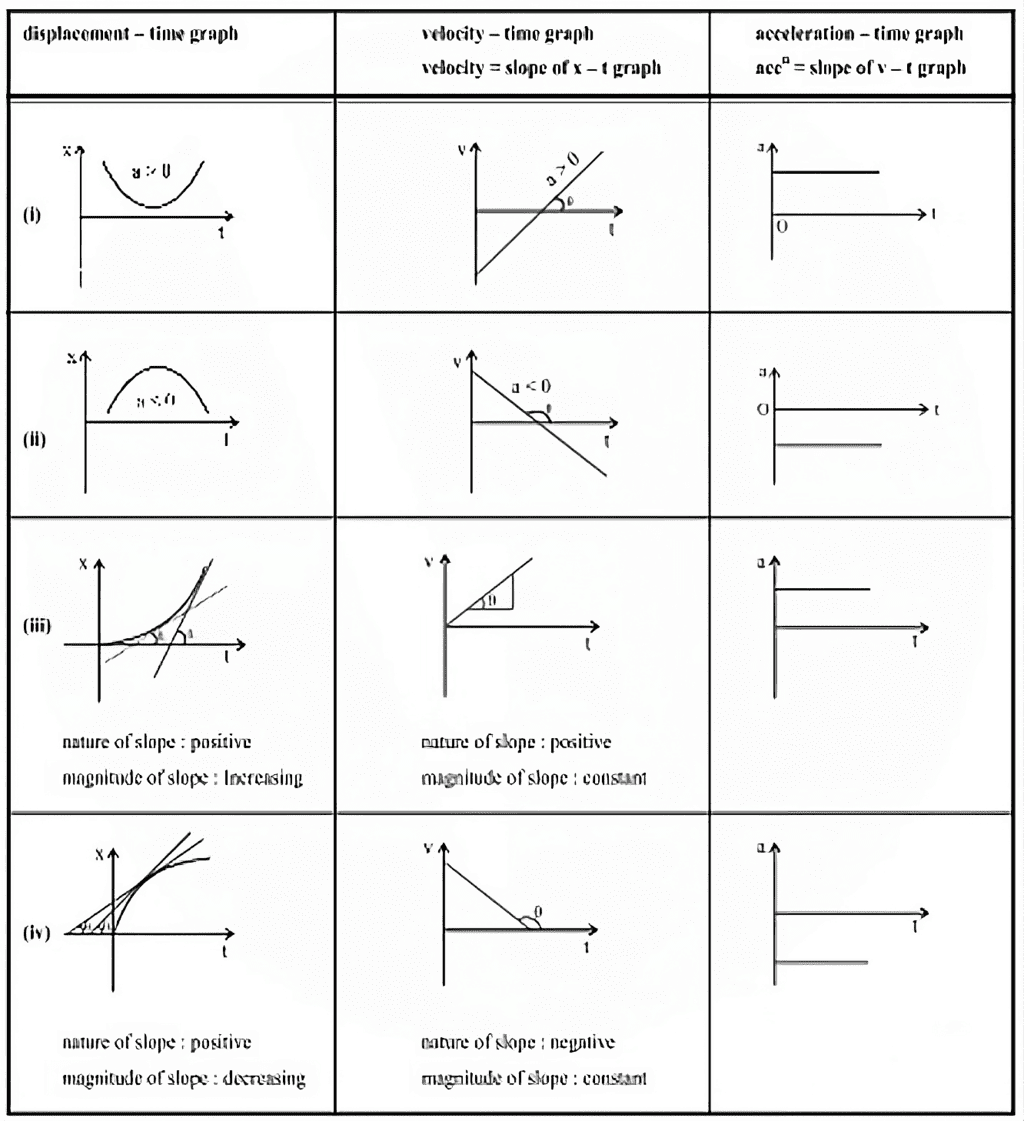
सारांश

यहां दिए गए सारांश में विषय के मुख्य बिंदुओं को संक्षेप में प्रस्तुत किया गया है।

• विषय की पहचान: इस अध्याय में अध्ययन किए गए मुख्य विषयों की पहचान की गई है।
• महत्व: प्रत्येक विषय का महत्व और इसके अध्ययन का उद्देश्य स्पष्ट किया गया है।
• प्रमुख परिभाषाएँ: कुछ महत्वपूर्ण परिभाषाएँ दी गई हैं जो विषय की समझ में सहायक हैं।
• आवश्यकता: इस अध्याय के अध्ययन की आवश्यकता और इसके लाभों पर चर्चा की गई है।

इस प्रकार, यह सारांश अध्याय के मुख्य तत्वों को संक्षेप में प्रस्तुत करता है और अध्ययन के लिए दिशा-निर्देश प्रदान करता है।