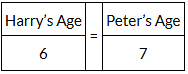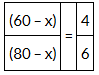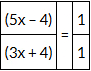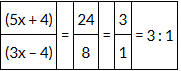Problems on Age | General Test Preparation for CUET UG - CUET Commerce PDF Download
| Table of contents |

|
| Introduction |

|
| Steps to Solve Age-Based Problems |

|
| Important Formulas |

|
| Solved Examples |

|
| Tips for Solving Age Problems |

|
Introduction
Problems on ages are commonly asked in almost all the competitive exams in the quantitative aptitude section. These problems involve solving mathematical questions where the relationship between the ages of different individuals is given. These problems often require setting up equations based on the given conditions and solving for the unknowns. Here's a breakdown of how to approach these problems.Steps to Solve Age-Based Problems
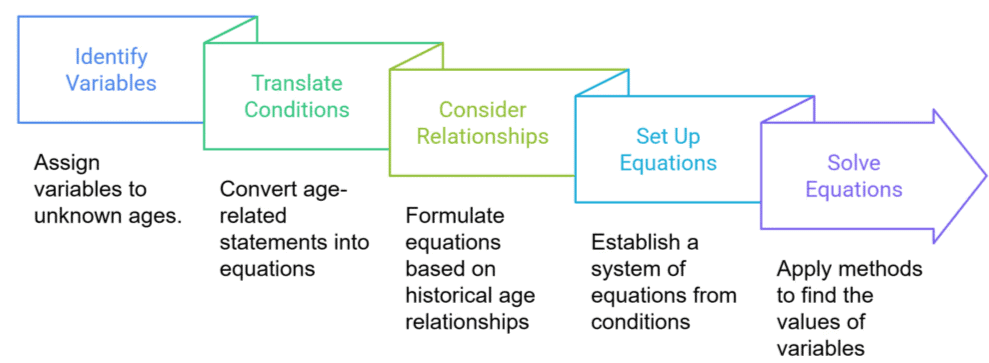
1. Identify the variables
The first step is to assign variables to the unknown ages. For example: Let the present age of person A be represented by x and B by y.
2. Translate the conditions into equations
If the problem says, "A's age is 7 years more than B's," then the equation would be: x = y + 7.
3. Consider relationships
If 7 years ago, B was twice as old as A, then: (y - 7) = 2 * (x - 7).
 |
Test: Problems On Ages - 1
|
Start Test |
4. Set up a system of equations
If "A's age is 3 years more than B's" and "5 years ago, A was twice as old as B," you would have:
x = y + 3 and (x - 5) = 2 * (y - 5)
5. Solve the system of equations
Use methods like substitution or elimination to solve the system of equations.
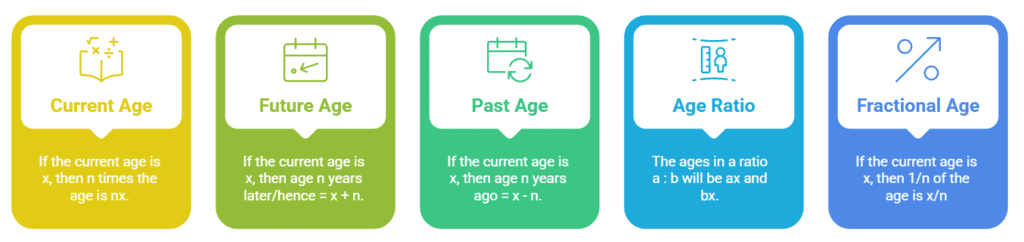
Important Formulas
Example Problem:
Q. Ten years ago, A was twice as old as B. Now, A is 5 years older than B. Find their present ages.Solution:
Let A’s present age = x and let B’s present age = y
Translate the conditions into equations:
From the first condition: Ten years ago, A was twice as old as B:
(x - 10) = 2 * (y - 10)
From the second condition: A is 5 years older than B:
x = y + 5
Solve the system of equations:
From x = y + 5, substitute x in the first equation:
(y + 5 - 10) = 2 * (y - 10)
y - 5 = 2y - 20
Simplify and solve for y:
y - 5 = 2y - 20
-5 + 20 = 2y - y
y = 15 , Substitute y = 15 into x = y + 5:
x = 15 + 5 = 20
So, A’s present age is 20 years, and B’s present age is 15 years.
 |
Download the notes
Problems on Age
|
Download as PDF |
Solved Examples
Example 1: Father is four times the age of his daughter. If after 5 years, he would be three times of daughter’s age, then further after 5 years, how many times he would be of his daughter’s age?
(a) 1.5 times
(b) 2 times
(c) 2.5 times
(d) 3 times
Ans: (c)
Let the daughter's age be x and father's age be 4x.
So as per question, 4x + 5 = 3(x + 5). So x = 10.
Hence present age of daughter is 10 years and present age of father is 40 years.
So after 5 + 5 = 10 years, daughter age would be 20 years and father’s age would be 50 years.
Hence father would be 50/20 = 2.5 times of daughter’s age.
Example 2: What is John’s present age, if after 10 years his age will be 5 times his age 5 years back.
(a) 6.2 years
(b) 7.7 years
(c) 8.7 years
(d) 10 years
Ans: (c)
1) Let John’s present age be x
2) John’s age before 5 years = (x - 5)
3) John’s age after 10 years = (x + 10)
We are given that, John’s age after 10 years (x + 10) is 5 times his age 5 years back (x – 5)
Therefore,
(x + 10) = 5 (x – 5)
Solving the equation, we get
x + 10 = 5x – 25
4x = 35
x = 8.75 years
Example 3: What is Aman's present age, if after 20 years his age will be 10 times his age 10 years back?
(a) 6.2 years
(b) 7.7 years
(c) 13.3 years
(d) 10 years
Ans: (c)
Let Aman's present age be x
Aman's age before 10 years = x - 10)
Aman's age after 20 years = (x + 20)
We are given that, Aman's age after 20 years (x + 20) is 10 times his age 10 years back (x – 10)
Therefore, (x + 20) = 10 (x – 10)
Solving the equation, we get x + 20 = 10x – 100
9x = 120, x = 13.3 years
Example 4: Rahul is 15 years elder than Rohan. If 5 years ago, Rahul was 3 times as old as Rohan, then find Rahul's present age.
(a) 32.5 years
(b) 27.5 years
(c) 25 years
(d) 24.9 years
Ans: (b)
1) Let age of Rohan be y
2) Rahul is 15 years elder than Rohan = (y + 15). So Rahul’s age 5 years ago = (y + 15 – 5)
3) Rohan’s age before 5 years = (y – 5)
5 years ago, Rahul is 3 times as old as Rohan
(y + 15 – 5) = 3 (y – 5)
(y + 10) = (3y – 15)
2y = 25
y = 12.5
Rohan’s age = 12.5 years
Rahul’s age = (y + 15) = (12.5 + 15) = 27.5 years
Example 5: Nisha is 15 years elder to Romi. If 5 years ago, Nisha was 3 times as old as Romi, then find Nisha’s present age.
(a) 29 years
(b) 27.5 years
(c) 26.2 years
(d) 29 years
Ans: (b)
Let age of Romi be y
Nisha is 15 years elder than Romi = (y + 15). So Nisha's age 5 years ago = (y + 15 – 5).
Romi's age before 5 years = (y – 5)
5 years ago, Nisha is 3 times as old as Romi
(y + 15 – 5) = 3 (y – 5)
(y + 10) = (3y – 15)
2y = 25 ⇒ y = 12.5
Romi's age = 12.5 years
Nisha's age = (y + 15) = (12.5 + 15) = 27.5 years.
Example 6: One year ago, ratio of Harry and Peter age’s was 5 : 6 respectively. After 4 years, this ratio becomes 6 : 7. How old is Peter?
(a) 25 years
(b) 26 years
(c) 31 years
(d) 35 years
Ans: (c)
Hint: If ages in the numerical are mentioned in ratio A : B, then A : B will be Ax and Bx.
We are given that age ratio of Harry : Pitter = 5 : 6
1) Harry’s age = 5x and Peter’s age = 6x
2) One year ago, their age was 5x and 6x. Hence at present, Harry’s age = 5x +1 and Peter’s age = 6x +1
3) After 4 years,
Harry’s age = (5x +1) + 4 = (5x + 5)
Peter’s age = (6x +1) + 4 = (6x + 5)
4) After 4 years, this ratio becomes 6 : 7. Therefore,
(5x + 5) / (6x + 5) = 6 / 7
7 (5x + 5) = 6 (6x + 5)
X = 5
Peter’s present age = (6x + 1) = (6 x 5 + 1) = 31 years
Harry’s present age = (5x + 1) = (5 x 5 + 1) = 26 years
Example 7: One year ago, the ratio of Honey and Piyush ages was 2: 3 respectively. After five years from now, this ratio becomes 4: 5. How old is Piyush now?
(a) 5 years
(b) 25 years
(c) 10 years
(d) 15 years
Ans: (c)
We are given that age ratio of Honey: Piyush = 2: 3
Honey’s age = 2x and Piyush’s age = 3x
One year ago, their age was 2x and 3x.
Hence at present, Honey's age = 2x +1 and Piyush's age = 3x +1
After 5 years, Honey’s age = (2x +1) + 5 = (2x + 6)
Piyush's age = (3x +1) + 5 = (3x + 6)
After 5 years, this ratio becomes 4: 5. Therefore,
(2x+6) / (3x+6) = 4/5
10x + 30 = 12x + 24 ⇒ x = 3
Piyush's present age = (3x + 1) = (3x 3 + 1) = 10 years
Honey's present age = (2x + 1) = (2x 3 + 1) = 7 years
Example 8: Age of mother 10 years ago was 3 times the age of her son. After 10 years, mother’s age will be twice that of his son. Find the ratio of their present ages.
(a) 11 : 7
(b) 9 : 5
(c) 7 : 4
(d) 7 : 3
Ans: (d)
We are given that, age of mother 10 years ago was 3 times the age of her son
So, let age of son be x and as mother’s age is 3 times the age of her son, let it be 3x, three years ago.
At present: Mother’s age will be (3x + 10) and son’s age will be (x + 10)
After 10 years: Mother’s age will be (3x + 10) +10 and son’s age will be (x + 10) + 10
Mother’s age is twice that of son
(3x + 10) +10 = 2 [(x + 10) + 10]
(3x + 20) = 2[x + 20]
Solving the equation, we get x = 20
We are asked to find the present ratio.
(3x + 10) : (x + 10) = 70 : 30 = 7 : 3
Example 9: The present age of A is three times that of B. In 10 years, the sum of their ages will be 100. What are their present ages?
A) A is 30 years, B is 10 years
B) A is 45 years, B is 15 years
C) A is 60 years, B is 20 years
D) A is 75 years, B is 25 years
Ans: (c)
Let the present age of A be x and the present age of B be y. we know the following two conditions:
x = 3y (The present age of A is three times that of B).
(x + 10) + (y + 10) = 100 (In 10 years, the sum of their ages will be 100).
Now, let's solve these equations.
From the first equation
x = 3y
Substitute x in the second equation.
Substitute x = 3y in (x + 10) + (y + 10) = 100:(3y + 10) + (y + 10) = 100
Simplify:
3y + 10 + y + 10 = 100
4y + 20 = 100
4y = 100 - 20
4y = 80
y = 80 / 4
y = 20
Find the age of A.
Since x = 3y, substitute y = 20:
x = 3 * 20 = 60
A’s present age is 60 years.
B’s present age is 20 years.
Example 10: Sharad is 60 years old and Santosh is 80 years ol(d) How many years ago was the ratio of their ages 4 : 6?
(a) 10 years
(b) 15 years
(c) 20 years
(d) 25 years
Ans: (c)
Here, we have to calculate: How many years ago the ratio of their ages was 4 : 6
Let us assume x years ago
At present: Sharad is 60 years and Santosh is 80 years
x years ago: Sharad’s age = (60 – x) and Santosh’s age = (80 – x)
Ratio of their ages x years ago was 4 : 66(60 – x) = 4(80 – x)
360 – 6x = 320 – 4x
x = 20
Therefore, 20 years ago, the ratio of their ages was 4 : 6
Example 11: Saransh is 50 years old and Nazma is 40 years old. How long ago was the ratio of their ages 3:2?
(a) 20 years
(b) 30 years
(c) 40 years
(d) 25 years
Ans: (a)
Here, we have to calculate: How many years ago the ratio of their ages was 3:2. Let us assume x years ago
At present: Saransh is 50 years and Nazma is 40 years
x years ago: Saransh’s age = (50 – x) and Nazma's age = (40 – x)
Given, the ratio of their ages was 3:2
(50-x) / (40-x) = 3/2
Solving, we get: x = 20
Therefore, the answer is 20 years.
Example 12: The ratio of Rohan’s age 4 years ago and Rahul’s age after 4 years is 1 : 1. If at present, the ratio of their ages is 5 : 3, then find the ratio between Rohan’s age 4 years hence and Rahul’s age 4 years ago.
(a) 1 : 3
(b) 3 : 1
(c) 4 : 3
(d) 3 : 4
Ans: (b)
Hint: If ages in the numerical are mentioned in ratio A : B, then A : B will be Ax and Bx
At present ratio of their ages = 5 : 3. Therefore, 5 : 3 will be 5x and 3x.
Rohan’s age 4 years ago = 5x – 4
Rahul’s age after 4 years = 3x + 4
Ratio of Rohan’s age 4 years ago and Rahul’s age after 4 years is 1 : 1
Therefore,
Solving, we get x = 4
We are asked to find the ratio between Rohan’s age 4 years hence and Rahul’s age 4 years ago.
Rohan’s age : (5x + 4)
Rahul’s age: (3x – 4)
Ratio of Rahul’s age and Rohan’s age
Example 13: The ratio of the present ages of Pranav and Qureshi is 4:5. Five years ago, the ratio of their ages was 7:9. Find their present ages? (In years)
(a) 40, 50
(b) 18, 25
(c) 40, 60
(d) 20, 25
Ans: (a)
Their present ages be 4X and 5X.
5 years ago, the ratio of their ages was 7:9, then (4X - 5) :( 5X - 5) = 7:9
X = 45 - 35 ⇒ X = 10.
Their present ages are: 40, 50
Example 14: 5 years ago, sister’s age was 5 times the age of her brother and the sum of present ages of sister and brother is 34 years. What will be the age of her brother after 6 years?
(a) 12 years
(b) 13.5 years
(c) 15 years
(d) 20 years
Ans: (c)
Let present age of brother be x and sister’s age be 34 – x.We are given, 5 years ago sister’s age was 5 times the age of her brother.
Therefore, (34 – x) – 5 = 5 (x – 5)
34 – x – 5 = 5x – 25
5x + x = 34 – 5 +25
6x = 54
x = 9
Future age (after 6 yrs) = (x + 6) = (9 + 6) = 15 years
Example 15: A man said to his son, "I was one-third of your present age when you were born". If the present age of the man is 48 years, find the present age of the son.
(a) 25.7 years
(b) 28 years
(c) 29.3 years
(d) 36 years
Ans: (d)
Present age of the son be P, he was born P years ago.
The age of the man was: (48 - P).
His age when the son was born should be equal to 1/3 of P.
(48 - P) =1/3 P ⇒ P = 36
Example 16: Dinesh is younger to Roshan by 9 years. If their ages are in the respective ratio of 4:5, how old is Dinesh?
(a) 36 years
(b) 23years
(c) 29 years
(d) Cannot be determined
Ans: (a)
Let Roshan's age be x years.
Then, Dinesh 's age = (x - 9) years.
(x - 9)/x = 4/5
x = 45 Hence, Dinesh's age = (x - 9) = 36 years.
Example 17: The ratio of Sara’s age 4 years ago and Vaishali’s age after 4 years is 1: 1. Presently, the ratio of their ages is 5: 3. Find the ratio between Sara’s age 4 years hence and Vaishali’s age 4 years ago.
(a) 1 : 3
(b) 3 : 1
(c) 4 : 3
(d) 3 : 4
Ans: (b)
Currently, the ratio of their ages is 5: 3. Suppose, their ages are: 5x and 3x.
Sara’s age 4 years ago = 5x – 4
Vaishali’s age after 4 years = 3x + 4
Ratio of Sara’s age 4 years ago and Vaishali's age after 4 years is 1 : 1
Therefore,
(5x - 4) / (3x + 4) = 1/1
Solving, we get x = 4
We are required to find the ratio between Sara’s age 4 years hence and Vaishali’s age 4 years ago.
Sara's age: (5x + 4)
Vaishali's age: (3x – 4)
Putting the value of x, we get:
(5x + 4) / (3x - 4) = 3/1 = 3:1
Example 18: The ratio of Raj’s age 6 years ago and Rahul’s age 6 years hence is 2:3. Presently, the ratio of their ages is 5:7. Find the ratio between Raj’s age 3 years hence and Rahul’s age 3 years ago.
(a) 5:9
(b) 3:5
(c) 4:7
(d) 6:5
Ans: (d)
Let Raj’s current age be 5x and Rahul’s current age be 7x (from the present age ratio).Six years ago, Raj’s age = 5x - 6; Six years hence, Rahul’s age = 7x + 6.
Given ratio:(5x − 6 ): (7x + 6) = 2 : 3.
Solve for x:
3(5x − 6)=2(7x + 6)
15x − 18=14x + 12
x = 30.Raj’s current age = 5x=150, Rahul’s current age = 7x = 210.
Raj’s age 3 years hence = 150 + 3 = 153.
Rahul’s age 3 years ago = 210 − 3 = 207.Ratio = 153 : 207 = 6:5
Example 19: The ratio of Meena’s age 5 years ago and Reena’s age after 5 years is 3:4. Currently, the ratio of their ages is 7:9. Find the ratio of Meena’s age 10 years hence and Reena’s age 10 years ago.
(a) 2:3
(b) 4:5
(c) 5:4
(d) 3:2
Ans: (c)
Let Meena’s current age be 7x and Reena’s current age be 9x (from the present age ratio).Five years ago, Meena’s age = 7x − 5; Five years hence, Reena’s age =9x + 5.
Given ratio: (7x − 5) : (9x + 5) = 3 : 4.
Solve for x:
4(7x − 5) = 3(9x + 5)
28x − 20 = 27x + 15
x = 35.
Meena’s current age = 7x = 245, Reena’s current age = 9x = 315.
Meena’s age 10 years hence = 245 + 10 = 255.
Reena’s age 10 years ago = 315 − 10 = 305.
Ratio = 255 : 305 = 5 : 4
Tips for Solving Age Problems
1. Pay close attention to the time references (past, present, future).
2. Carefully translate the verbal statements into algebraic expressions.
3. Set up the equations logically and use algebraic methods to solve them.
|
164 videos|603 docs|945 tests
|
FAQs on Problems on Age - General Test Preparation for CUET UG - CUET Commerce
| 1. What are the basic steps to solve age-based problems? |  |
| 2. What important formulas are used in age-based problems? |  |
| 3. Can you provide an example of an age-based problem and its solution? |  |
| 4. What tips can help effectively solve age problems? |  |
| 5. How can I practice age-related problems effectively? |  |