महत्वपूर्ण सूत्र: संख्या प्रणाली | CSAT की तैयारी (हिंदी) - UPSC PDF Download

• अलजेब्रा में महत्वपूर्ण सूत्र: अलजेब्रा गणित की एक शाखा है जो संख्याओं के लिए अक्षरों का स्थानापन्न करती है।
• एक अलजेब्रा समीकरण एक तराजू का प्रतिनिधित्व करती है, जिसमें तराजू के एक पक्ष पर जो कुछ किया जाता है, वही दूसरे पक्ष पर भी किया जाता है।
• कुछ प्रमुख सूत्र:
  • (a + b)(a - b) = (a² - b²)
  • (a + b)² = a² + 2ab + b²
  • (a - b)² = a² - 2ab + b²
  • (a + b + c)² = a² + b² + c² + 2(ab + bc + ca)

• 1 + 2 + 3 + ... + n = n(n + 1)/2
• उदाहरण: पहले 35 प्राकृतिक संख्याओं का योग ज्ञात करें।
  • S = [35(35 + 1)]/2 = 630
• (1² + 2² + 3² + ... + n²) = n(n + 1)(2n + 1)/6
• उदाहरण: पहले 40 प्राकृतिक संख्याओं के वर्गों का योग ज्ञात करें।
  • Σ40² = (40/6)(40 + 1)(2x40 + 1) = 22140
• सभी संख्याओं का योग ज्ञात करना:
• संगणक संख्याओं का योग = [n(n + 1)]²/4

• Σ(5 से 14) = Σ(1 से 14) - Σ(1 से 4) = 11025 - 100 = 10925

• उदाहरण: 1 से 50 तक विषम संख्याओं का योग ज्ञात करें।
  • n = 25, S25 = 25² = 625

• उदाहरण: 1 से 50 तक सम संख्याओं का योग ज्ञात करें।
  • n = 25, S25 = 25(25 + 1) = 650

• उदाहरण: 100! में 7 की उच्चतम शक्ति ज्ञात करें।
  • Highest power of 7 in 100! = [100/7] + [100/49] = 16

• HCF * LCM = दो संख्याओं का गुणनफल
• 96, 36, और 18 का HCF ज्ञात करें:
  • HCF = 6
• 42 और 70 का LCM ज्ञात करें:
  • LCM = 210

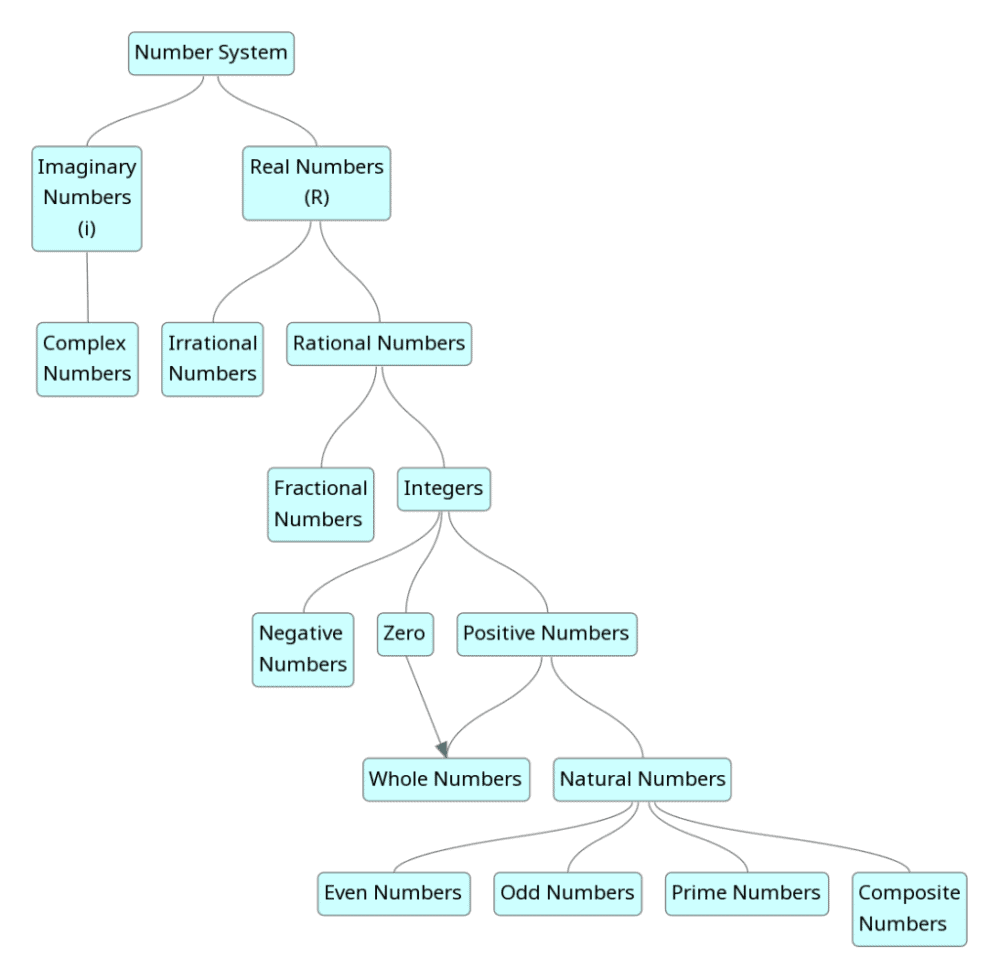
• प्राकृतिक संख्याएँ: {1, 2, 3, ...}
• पूर्णांक: {0, 1, 2, ...}
• तर्कसंगत संख्याएँ: a/b (जहाँ b ≠ 0)
• असंगत संख्याएँ: अनुपात रूप में नहीं लिखी जा सकतीं।
• प्राइम संख्याएँ: केवल 1 और स्वयं के दो गुणक वाली संख्याएँ।

• 2 द्वारा भाग देने की स्थिति: अंतिम अंक 0, 2, 4, 6, या 8 होना चाहिए।
• 3 द्वारा भाग देने की स्थिति: संख्याओं का योग 3 से विभाज्य होना चाहिए।
• 4 द्वारा भाग देने की स्थिति: अंतिम दो अंकों का योग 4 से विभाज्य होना चाहिए।
• 5 द्वारा भाग देने की स्थिति: अंतिम अंक 0 या 5 होना चाहिए।

• 7248 को 4 द्वारा विभाजित किया जा सकता है।
• 7248 को 2 द्वारा विभाजित किया जा सकता है।
• 7248 को 8 द्वारा विभाजित नहीं किया जा सकता है।

संख्या प्रणाली पर अन्य विषयों के लिए लिंक:

• परिचय: संख्या प्रणाली
• महत्वपूर्ण अवधारणाएँ: संख्या प्रणाली - 1
• महत्वपूर्ण अवधारणाएँ: संख्या प्रणाली - 2
• आधार प्रणालियों का अवलोकन: संख्या प्रणाली
• भागफल के नियम: परिचय और अवधारणा
• HCF और LCM

संख्यात्मक प्रणाली एक संख्या को संख्या रेखा पर प्रदर्शित करने की एक विधि है। संख्यात्मक प्रणाली संख्याओं को लिखने या व्यक्त करने का एक तंत्र है। इस पृष्ठ पर संख्यात्मक प्रणाली के सूत्रों और परिभाषाओं का विवरण है।

यहाँ उन महत्वपूर्ण सूत्रों की एक सूची दी गई है, जिन्हें उम्मीदवारों को परीक्षा में सफलतापूर्वक उत्तीर्ण करने के लिए महारत हासिल करनी चाहिए।

अलजेब्रा गणित की एक शाखा है जो संख्याओं के लिए अक्षरों का स्थानापन्न करती है। एक अलजेब्राई समीकरण एक तराजू का चित्रण करता है, जिसमें तराजू के एक पक्ष पर जो कुछ किया जाता है, वही दूसरी ओर भी किया जाता है।

• (a + b)(a - b) = (a² - b²)
• (a + b)² = (a² + b² + 2ab)
• (a - b)² = (a² + b² - 2ab)
• (a + b + c)² = a² + b² + c² + 2(ab + bc + ca)
• (a³ + b³) = (a + b)(a² - ab + b²)
• (a³ - b³) = (a - b)(a² + ab + b²)
• (a³ + b³ + c³ - 3abc) = (a + b + c)(a² + b² + c² - ab - ac - bc) ⇒ जब a + b + c = 0, तब a³ + b³ + c³ = 3abc
• (a + b)ⁿ = Σ (nCk) aⁿ⁻ᵏ bᵏ

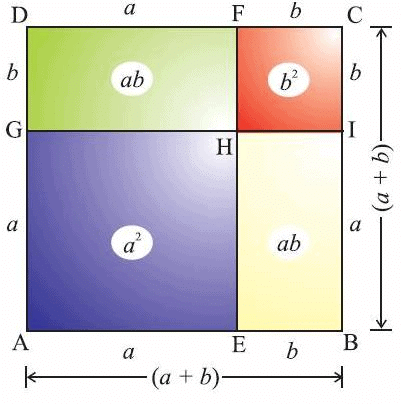
(a + b)² = a² + 2ab + b²

(a + b)² सूत्र दो संख्याओं के योग का वर्ग निकालने के लिए उपयोग किया जाता है। (a + b)² के रूप में बायनॉमियल का सूत्र निकालने के लिए, हम केवल (a + b) को स्वयं से गुणा करते हैं।

• इसलिए, (a + b)² सूत्र है: (a + b)² = a² + 2ab + b²

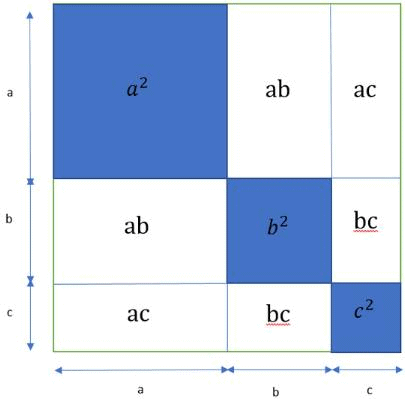
(a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ca

(a + b + c)² सूत्र तीन संख्याओं के वर्गों के योग को बिना वास्तव में वर्ग की गणना किए निकालने के लिए उपयोग किया जाता है।

• (1 + 2 + 3 + ... + n) = n(n + 1)/2
• उदाहरण: पहले 35 प्राकृतिक संख्याओं का योग निकालें। समाधान: यहाँ, n = 35
• प्राकृतिक संख्याओं का योग सूत्र है: S = [n(n + 1)]/2
• S = [35(35 + 1)]/2 = 630

• (1² + 2² + 3² + ... + n²) = n(n + 1)(2n + 1)/6
• उदाहरण: पहले 40 प्राकृतिक संख्याओं के वर्गों का योग निकालें। समाधान: यहाँ, n = 40
• Σn² = [n(n + 1)(2n + 1)]/6
• Σ40² = (40/6)(41)(81) = 22140

• (1³ + 2³ + 3³ + ... + n³) = (n(n + 1)/2)²
• उदाहरण: प्राकृतिक संख्याओं का योग 5 से 14 तक के घन निकालें।
• हम पहले 14 प्राकृतिक संख्याओं के घन का योग निकालेंगे और फिर पहले 4 प्राकृतिक संख्याओं के घन का योग निकालेंगे।
• पहले 14 प्राकृतिक संख्याओं के घन का योग = 11025
• पहले 4 प्राकृतिक संख्याओं के घन का योग = 100
• इस प्रकार, 5 से 14 तक प्राकृतिक संख्याओं के घनों का योग = 10925।

• पहले n विषम संख्याओं का योग = n²
• उदाहरण: 1 से 50 तक विषम संख्याओं का योग निकालें।
• हम जानते हैं कि 1 से 50 के बीच 25 विषम संख्याएँ हैं।
• इसलिए, n² के सूत्र का उपयोग करके, S25 = 25² = 625।

समाधान: हम जानते हैं कि 1 से 50 के बीच 25 विषम संख्याएँ हैं। इस प्रकार, n² के सूत्र का उपयोग करके, S25 = 25² = 625।

इस प्रकार, a = 1, l = 49, और n = 25। S25 = (25/2) × [1 49]

• पहली n सम संख्याओं का योग = n (n + 1) उदाहरण: 1 से 50 तक के सम संख्याओं का योग क्या है? हल: हमें पता है कि, 1 से 50 तक, 25 सम संख्याएँ हैं। इस प्रकार, n = 25। सम संख्याओं के योग के सूत्र के अनुसार; Sn = n(n + 1) Sn = 25(25 + 1) = 25 × 26 = 650

उदाहरण: 1 से 50 तक के सम संख्याओं का योग क्या है? हल: हमें पता है कि, 1 से 50 तक, 25 सम संख्याएँ हैं। इस प्रकार, n = 25। सम संख्याओं के योग के सूत्र के अनुसार; Sn = n(n + 1) Sn = 25(25 + 1) = 25 × 26 = 650

• n की सबसे बड़ी शक्ति m! में है [m/n] + [m/n²] + [m/n³] ….. जहाँ, [x] x से कम या उसके बराबर सबसे बड़ा पूर्णांक है। उदाहरण: 100! में 7 की सबसे बड़ी शक्ति ज्ञात करें। 100! में 7 की सबसे बड़ी शक्ति = [100/7] + [100/49] = 16

n की सबसे बड़ी शक्ति m! में है [m/n] + [m/n²] + [m/n³] ….. जहाँ, [x] x से कम या उसके बराबर सबसे बड़ा पूर्णांक है। उदाहरण: 100! में 7 की सबसे बड़ी शक्ति ज्ञात करें। 100! में 7 की सबसे बड़ी शक्ति = [100/7] + [100/49] = 16

• n! में शून्य की संख्या ज्ञात करने के लिए n! में 5 की सबसे बड़ी शक्ति ज्ञात करें। उदाहरण: 23! में पीछे के शून्य की संख्या क्या है? [23/5] = 4। यह 5 से कम है, इसलिए हम यहाँ रुकते हैं। उत्तर 4 है।
• यदि n भिन्न अंकों की सभी संभावित क्रमबद्धताएँ एकत्रित की गईं, तो उनका योग = (n-1)! × (n अंकों का योग) × (11111… n बार) उदाहरण: 1, 3, 5, 7 अंकों का उपयोग करके, जो सभी एक साथ हैं और जिनमें कोई अंक पुनरावृत्त नहीं है, द्वारा बनाई गई सभी संख्याओं का योग क्या होगा? हल: सभी दिए गए n अंकों द्वारा बनी संख्याओं का योग है (सभी n अंकों का योग) × (n - 1)! × (111…..n बार)। यहाँ n = 4, और 4 अंकों का योग = 16। 1, 3, 5, 7 अंकों द्वारा बनाई गई सभी संख्याओं का योग = (16) × (4 – 1)! × (1111) = 16 × 3! × 1111

यदि n भिन्न अंकों की सभी संभावित क्रमबद्धताएँ एकत्रित की गईं, तो उनका योग = (n-1)! × (n अंकों का योग) × (11111… n बार) उदाहरण: 1, 3, 5, 7 अंकों का उपयोग करके, जो सभी एक साथ हैं और जिनमें कोई अंक पुनरावृत्त नहीं है, द्वारा बनाई गई सभी संख्याओं का योग क्या होगा? हल: सभी दिए गए n अंकों द्वारा बनी संख्याओं का योग है (सभी n अंकों का योग) × (n - 1)! × (111…..n बार)। यहाँ n = 4, और 4 अंकों का योग = 16। 1, 3, 5, 7 अंकों द्वारा बनाई गई सभी संख्याओं का योग = (16) × (4 – 1)! × (1111) = 16 × 3! × 1111

यदि संख्या को इस रूप में दर्शाया जा सकता है N = ap∗ bq ∗ cr, तो N के कारकों की संख्या (p + 1) * (q + 1) * (r + 1) होगी।

सभी कारकों का योग: उदाहरण: 98 के कारकों की संख्या ज्ञात करें और सभी कारकों का योग और गुणनफल भी ज्ञात करें।

हल: पहले संख्या 98 को प्राइम फैक्टराइजेशन में लिखें। अर्थात्, 98 = 2 × 49 = 2 × 7 × 7 = 2¹ × 7²।

• यहां A = 2, B = 7, p = 1, q = 2
• 98 के लिए कारकों की संख्या = (p + 1)(q + 1) = 2 × 3 = 6
• 98 के सभी कारकों का योग = 3 × 57 = 171
• संख्या 98 के सभी कारकों का गुणनफल = (98)^6/2 = 941192

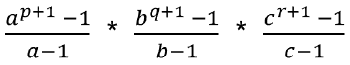
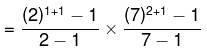
यदि कारकों की संख्या विषम है, तो N एक पूर्ण वर्ग है। उदाहरण: 4500 के विषम, सम, पूर्ण वर्ग, पूर्ण घन कारकों की संख्या ज्ञात करें।

4500 = 45 × 100 = 9 × 5 × 10 × 10 = 3 × 3 × 5 × 5 × 2 × 5 × 2 = 2² × 3² × 5³।

• यहां, A = 2, B = 3, C = 5, p = 2, q = 2 और r = 3।
• यहां विषम संख्याएँ 3 और 5 हैं।
• 4500 के विषम कारकों की संख्या = (q + 1)(r + 1) = 3 × 4 = 12
• ∴ कुल कारकों की संख्या = (p + 1)(q + 1)(r + 1) = 3 × 3 × 4 = 36
• सम कारकों की संख्या = (कुल कारकों की संख्या - विषम कारकों की संख्या) = 36 – 12 = 24
• 4500 के पूर्ण वर्ग कारकों की संख्या = 2 × 2 × 2 = 8
• 4500 के पूर्ण घन कारकों की संख्या = 1 × 1 × 2 = 2

मान लीजिए एक संख्या N है और यदि इसमें n गुणनखण्ड हैं, जिसमें संख्या N और 1 शामिल हैं, तो गुणनखण्डों के जोड़ों की संख्या n/2 होगी। यदि N एक पूर्ण वर्ग है, तो जोड़ों की संख्या (जिसमें वर्गमूल भी शामिल है) (n + 1)/2 होगी। उदाहरण: आप 36 को इसके दो गुणनखण्डों के गुणन के रूप में कितने तरीकों से व्यक्त कर सकते हैं? 36 का प्राथमिक गुणनखण्डन इस प्रकार है: 36 = 2² × 3²। 36 के गुणनखण्डों की संख्या होगी (2 + 1)(2 + 1) = 9 (अर्थात् गुणनखण्ड हैं 1, 2, 3, 4, 6, 9, 12, 18, 36)। चूंकि हमसे कुल तरीकों की संख्या पूछी गई है, इसलिए हम 36 के वर्गमूल यानी 6 को भी शामिल करते हैं। इस प्रकार, आप 36 को इसके दो गुणनखण्डों के गुणन के रूप में व्यक्त करने के (9 + 1)/2 = 5 तरीके हैं।

यदि संख्या को इस प्रकार व्यक्त किया जा सकता है: N = 2^p × a^q × b^r ..., जहाँ 2 की शक्ति p है और a, b प्रमुख संख्या हैं, तो: (i) N के सम गुणनखण्डों की संख्या = p (1 + q) (1 + r) ... (ii) N के विषम गुणनखण्डों की संख्या = (1 + q) (1 + r)...

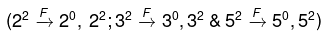
जब हमसे पूछा जाता है कि समीकरण X² - Y² = N के लिए कितने सकारात्मक पूर्णांक समाधान संभव हैं, तो इसके 4 मामले हो सकते हैं। आइए हम इन्हें एक-एक करके उदाहरणों द्वारा समझते हैं:

• मामला 1: N एक विषम संख्या है और पूर्ण वर्ग नहीं है
• मामला 2: N एक विषम संख्या है और पूर्ण वर्ग है
• मामला 3: N एक सम संख्या है और पूर्ण वर्ग नहीं है
• मामला 4: N एक सम संख्या है और पूर्ण वर्ग है

मामला 1: N एक विषम संख्या है और पूर्ण वर्ग नहीं है

सकारात्मक पूर्णांक समाधानों की कुल संख्या होगी = (N के गुणकों की कुल संख्या) / 2

उदाहरण: समीकरण X² – Y² = 135 के लिए कितने सकारात्मक पूर्णांक समाधान संभव हैं?

135 के गुणकों की कुल संख्या = 1, 3, 5, 9, 15, 27, 45 और 135 है, जो कि 8 है। इसलिए, सकारात्मक पूर्णांक समाधानों की कुल संख्या = 8/2 = 4।

मामला 2: N एक विषम संख्या है और पूर्ण वर्ग है

सकारात्मक पूर्णांक समाधानों की कुल संख्या होगी = [(N के गुणकों की कुल संख्या) – 1] / 2

उदाहरण: समीकरण X² – Y² = 121 के लिए कितने सकारात्मक पूर्णांक समाधान संभव हैं?

121 के गुणकों की कुल संख्या = 1, 11 और 121 है, जो कि 3 है। इसलिए, सकारात्मक पूर्णांक समाधानों की कुल संख्या = (3-1) / 2 = 1।

मामला 3: N एक सम संख्या है और पूर्ण वर्ग नहीं है

सकारात्मक पूर्णांक समाधानों की कुल संख्या होगी = [N/4 के गुणकों की कुल संख्या] / 2

उदाहरण: समीकरण X² – Y² = 160 के लिए कितने सकारात्मक पूर्णांक समाधान संभव हैं?

40 के गुणकों की कुल संख्या = 1, 2, 4, 5, 8, 10, 20 और 40 है, जो कि 8 है (क्योंकि N = 160 और N/4 = 40)। इसलिए, सकारात्मक पूर्णांक समाधानों की कुल संख्या = 8/2 = 4।

मामला 4: N एक सम संख्या है और पूर्ण वर्ग है

सकारात्मक पूर्णांक समाधानों की कुल संख्या होगी = {[N/4 के गुणकों की कुल संख्या] – 1} / 2

उदाहरण: समीकरण X² – Y² = 256 के लिए कितने सकारात्मक पूर्णांक समाधान संभव हैं?

64 के गुणकों की कुल संख्या = 1, 2, 4, 8, 16, 32 और 64 है, जो कि 7 है (क्योंकि N = 256 और N/4 = 64)। इसलिए, (7-1) / 2 = 3 सकारात्मक पूर्णांक समाधान।

EduRev टिप: एक संख्या को दो वर्गों के योग के रूप में लिखा जा सकता है जबकि 4k³ के रूप के प्रमुख गुणांक शामिल होते हैं, बशर्ते कि उन प्रमुख गुणांक को सम शक्ति में उठाया गया हो।

ab में अंकों की संख्या = [b logm(a)] 1; जहाँ m संख्या का आधार है और [.] सबसे बड़ा पूर्णांक फ़ंक्शन को दर्शाता है।

• बुनियादी योग गुण: (i) पहले n विषम संख्याओं का योग n² है (ii) पहले n सम संख्याओं का योग n(n + 1) है (iii) 1 + 2 + 3 + 4 + 5 + … + n = n(n + 1)/2 है (iv) (1² + 2² + 3² + ….. + n²) = n(n + 1)(2n + 1)/6 है (v) (1³ + 2³ + 3³ + ….. + n³) = (n(n + 1)/2)² है।

एन के गुणकों का गुणनफल Na/2 द्वारा दिया गया है, जहाँ 'a' गुणकों की संख्या है।

• अंतिम दो अंकों का मूल्य a², (50 – a)², (50 + a)², (100 – a)² में समान होता है। प्रत्येक संख्या को (50n ± x) के रूप में लिखा जा सकता है, जहाँ x 0 से 25 के बीच का एक संख्या है। यहाँ 50n का मतलब है 50 का कोई गुणांक जैसे 0, 50, 100, 150, …… 0 से 25 = (0 से 25) स्वयं। 25 से 50 = 50 – (25 से 0) 50 से 75 = 50 (0 से 25) 75 से 100 = 100 – (25 से 0) 100 से 125 = 100 (0 से 25) 125 से 150 = 150 – (25 से 0) और इसी तरह।

लेकिन यह हमें किसी भी वर्ग के अंतिम दो अंकों को खोजने में कैसे मदद करता है? (50n ± x)² = 2500n² ± 100nx + x²। 2500n² और 100nx के प्रत्येक के अंतिम दो अंक 00 होंगे। इसलिए, RHS और इस प्रकार LHS के अंतिम दो अंक x² के अंतिम दो अंक होंगे।

उदाहरण: 268² के अंतिम दो अंक क्या हैं? 268 = 50 × 5 + 18। इसलिए, 268² के अंतिम दो अंक 182 के अंतिम दो अंकों के समान होंगे, अर्थात 24।

उदाहरण: 278² के अंतिम दो अंक क्या हैं? जबकि आप 278 = 50 × 5 + 28 पर विचार कर सकते हैं, यह 278 = 50 × 6 – 22 पर विचार करेगा, जिससे x 0 से 25 के बीच होगा। इसलिए, 278² के अंतिम दो अंक 222 के अंतिम दो अंकों के समान होंगे, अर्थात 84।

लेकिन यह हमें किसी भी वर्ग के अंतिम दो अंकों को खोजने में कैसे मदद करता है? (50n ± x)² = 2500n² ± 100nx x² 2500n² और 100nx के अंतिम दो अंक 00 होंगे। इस प्रकार, RHS के अंतिम दो अंक, और इसलिए LHS के अंतिम दो अंक, x² के अंतिम दो अंक होंगे।

268 = 50 × 5 18। इस प्रकार, 268² के अंतिम दो अंक 182 के अंतिम दो अंकों के समान होंगे, अर्थात् 24।

जब आप 278 = 50 × 5 28 को मान सकते हैं, तो यह 278 = 50 × 6 – 22 को मानता है, जो 0 से 25 के बीच x होगा। इस प्रकार, 278² के अंतिम दो अंक 222 के अंतिम दो अंकों के समान होंगे, अर्थात् 84।

• यदि संख्या को 210n के रूप में लिखा जाए: (i) जब n विषम है, तो अंतिम 2 अंक 24 हैं। (ii) जब n सम है, तो अंतिम 2 अंक 76 हैं।
• पूर्णांक: सभी संख्या जो दशमलव स्थान नहीं रखती हैं, उन्हें पूर्णांक कहा जाता है। Z = {∞…….-3, -2, -1, 0, 1, 2, 3………∞}
  • सकारात्मक पूर्णांक: 1, 2, 3, 4….. सभी सकारात्मक पूर्णांकों का समूह है।
  • ऋणात्मक पूर्णांक: −1, −2, −3….. सभी ऋणात्मक पूर्णांकों का समूह है।
  • गैर-सकारात्मक और गैर-ऋणात्मक पूर्णांक: 0 न तो सकारात्मक है और न ही ऋणात्मक।
• अव्यवस्थित संख्याएँ: यह एक संख्या है जिसे अनुपात रूप (या भिन्न) में नहीं लिखा जा सकता। अव्यवस्थित संख्याएँ गैर-समाप्ति और गैर-आवृत्त भिन्न हैं। उदाहरण: 22 = 1.414
• जटिल संख्याएँ: जटिल संख्याएँ सेट हैं {a + bi}, जहाँ a और b वास्तविक संख्याएँ हैं और i काल्पनिक इकाई है।

• 2 द्वारा विभाज्यता → एक संख्या जो सम होती है या जिसकी अंतिम अंक सम संख्या होती है अर्थात् 0, 2, 4, 6, और 8।
• 3 द्वारा विभाज्यता → संख्या के सभी अंकों का योग 3 से विभाज्य होना चाहिए।
• 4 द्वारा विभाज्यता → संख्या के अंतिम दो अंकों से बनी संख्या 4 से विभाज्य होनी चाहिए या 00 होनी चाहिए।
• 5 द्वारा विभाज्यता → 0 या 5 को एकांक स्थान के अंक के रूप में रखने वाली संख्याएँ।
• 6 द्वारा विभाज्यता → एक संख्या जो 2 और 3 दोनों से विभाज्य होती है।
• 7 द्वारा विभाज्यता → संख्या के अंतिम अंक का दो गुना घटाने पर जो शेष अंक होते हैं, वह 7 का गुणांक देना चाहिए।
• 8 द्वारा विभाज्यता → संख्या के अंतिम तीन अंकों से बनी संख्या 8 से विभाज्य होनी चाहिए या 000 होनी चाहिए।
• 9 द्वारा विभाज्यता → संख्या के सभी अंकों का योग 9 से विभाज्य होना चाहिए।
• 10 द्वारा विभाज्यता → 10 के लिए विभाज्यता नियम यह कहता है कि कोई भी संख्या जिसकी अंतिम अंक 0 है, वह 10 से विभाज्य है।
• 11 द्वारा विभाज्यता → एक संख्या 11 से विभाज्य है यदि इसकी विषम अंकों का योग और सम अंकों का योग का अंतर 0 या 11 हो।
• 12 द्वारा विभाज्यता → एक संख्या जो 3 और 4 दोनों से विभाज्य होती है।
• 13 द्वारा विभाज्यता → किसी दिए गए संख्या के लिए, यह जांचने के लिए कि यह 13 से विभाज्य है या नहीं, हमें संख्या के अंतिम अंक का चार गुना जोड़ना होगा और प्रक्रिया को तब तक दोहराना होगा जब तक कि हमें एक दो अंकीय संख्या न मिले। अब देखें कि क्या वह दो अंकीय संख्या 13 से विभाज्य है या नहीं। यदि यह विभाज्य है, तो दी गई संख्या 13 से विभाज्य है।
• 14 द्वारा विभाज्यता → एक संख्या जो 2 और 7 दोनों से विभाज्य होती है।
• 16 द्वारा विभाज्यता → अंतिम चार अंक जो 16 से विभाज्य होते हैं।
• 27 द्वारा विभाज्यता → 3 के समूहों का योग (दाएं से बाएं लिया गया) 27 से विभाज्य होना चाहिए।

उत्तर:

(i) संख्या 7248 के सबसे दाहिने सिरे पर 48 है, जो 4 से पूरी तरह विभाज्य है। जब हम 48 को 4 से विभाजित करते हैं, तो हमें 12 मिलता है।

(ii) संख्या 7248 के इकाई स्थान पर 8 है, जो एक सम संख्या है, इसलिए 7248 2 से विभाज्य है।

(iii) 7248 8 से विभाज्य है क्योंकि 7248 के सैंकड़ा स्थान, दस स्थान और इकाई स्थान पर 248 है, जो 8 से पूरी तरह विभाज्य है।

प्रश्न 3. बिना वास्तविक विभाजन के, पता करें कि 235932 (i) 4 से और (ii) 8 से विभाज्य है या नहीं। उत्तर:

(i) 235932 के सबसे दाहिने सिरे पर अंतिम दो अंकों द्वारा निर्मित संख्या 32 है।

(ii) 235932 के सबसे दाहिने सिरे पर अंतिम तीन अंकों द्वारा निर्मित संख्या 932 है।

नियम के अनुसार, यदि किसी संख्या के अंकों का योग 9 का गुणांक है, तो वह 9 से विभाज्य है। 998 के अंकों का योग: 9 + 9 + 8 = 26, 26 9 का गुणांक नहीं है। इसलिए, 998 9 से विभाज्य नहीं है।

नियम के अनुसार, एक संख्या में, यदि विषम स्थानों पर अंकों का योग और सम स्थानों पर अंकों का योग समान हैं या वे 11 से विभाज्य संख्या से भिन्न हैं, तो संख्या 11 से विभाज्य है। 1782 में, विषम स्थानों पर अंकों का योग: 1 + 8 = 9, 1782 में, सम स्थानों पर अंकों का योग: 7 + 2 = 9। 1782 में, विषम स्थानों पर अंकों का योग और सम स्थानों पर अंकों का योग समान है। इसलिए, 1782 11 से विभाज्य है।

उदाहरण 1: 96, 36, और 18 का HCF खोजें।

उदाहरण 2: 42 और 70 का HCF खोजें।

उदाहरण 3: 144, 630, और 756 के अंकों का HCF खोजें।

144 = 24 × 32, 630 = 2 × 32 × 5 × 7, 756 = 22 × 33 × 7। इसलिए, 144, 630, और 756 का HCF = 2 × 32 = 18।

उदाहरण 4: 96, 36, और 18 का LCM खोजें।

96 = 2 × 2 × 2 × 2 × 2 × 3 = 2⁵ × 3¹
36 = 2 × 2 × 3 × 3 = 2² × 3²
18 = 2 × 3 × 3 = 2¹ × 3²

इसलिए, 96, 36 और 18 का LCM सभी प्रधान गुणकों की सबसे उच्च शक्तियों के गुणनफल का परिणाम है, अर्थात् 2⁵ × 3² = 32 × 9 = 288। इसका अर्थ है, 288 वह सबसे छोटा पूर्णांक है जो 96, 36 और 18 से बिना किसी शेष के विभाज्य है।

उदाहरण 5: 42 और 70 का LCM खोजें।

इसलिए, LCM = 2 × 3 × 5 × 7 = 210। प्रधान गुणनखंड विधि के अलावा, दिए गए संख्याओं का LCM खोजने का एक और तरीका है, जिसे दीर्घ विभाजन विधि कहा जाता है। यह विधि तीन या अधिक संख्याओं के लिए LCM जल्दी प्राप्त करने में सहायक होती है।

यहाँ, हमें 48 और 300 का LCM निकालना है।

48 = 2 × 2 × 2 × 2 × 3 = 2⁴ × 3¹
300 = 2 × 2 × 3 × 5 × 5 = 2² × 3¹ × 5²

सभी संख्याओं को सूचीबद्ध करें, जितनी बार वे प्रकट होती हैं, सबसे अधिक बार किसी एक संख्या के लिए, और उन्हें एक साथ गुणा करें ताकि LCM प्राप्त हो सके। इस प्रकार, 2⁴ × 3¹ × 5² = 1200।

इसलिए, 48 और 300 का LCM 1200 है।

अब, हमें 12, 18, 30 का LCM निकालना है। पहले, उपरोक्त तीन संख्याओं के प्रधान गुणांकों को खोजें।

12 = 2 × 2 × 3 = 2² × 3¹
18 = 2 × 3 × 3 = 2¹ × 3²
30 = 2 × 3 × 5 = 2¹ × 3¹ × 5¹

अब, सभी प्रधान संख्याओं को सूचीबद्ध करें, जितनी बार वे प्रकट होती हैं, सबसे अधिक बार किसी एक संख्या के लिए, और उन्हें एक साथ गुणा करें ताकि LCM प्राप्त हो सके। इस तरह, 2² × 3² × 5¹ = 180।

उच्च शक्ति वाले प्रत्येक प्रधान संख्या को गुणा करने के लिए घातांक का उपयोग करें। इस प्रकार, 2² × 3² × 5¹ = 180।

इसलिए, 12, 18, 30 का LCM 180 है।