सारांश: अनुपात और समानुपात | CSAT की तैयारी (हिंदी) - UPSC PDF Download
CSAT में महत्व
CSAT में महत्व
अनुपात और अनुपात के मूल बातें CSAT परीक्षाओं के लिए बहुत महत्वपूर्ण हैं। प्रश्न सीधे नहीं पूछे जाते हैं, लेकिन इस अध्याय में उपयोग किए गए सिद्धांत CSAT परीक्षा में महत्वपूर्ण भूमिका निभाते हैं। यह डेटा व्याख्या के लिए भी एक आधार के रूप में काम करता है। जिन विषयों से सामान्यतः प्रश्न पूछे जाते हैं, वे निम्नलिखित हैं:
- दूध और पानी का अनुपात।
- वेतन और व्यय का अनुपात।
- मिश्रण।
- भागीदारी।
वर्ष 2023 और 2022 में दो प्रश्न पूछे गए थे, लेकिन वर्षों 2021-2018 में इस अध्याय से कम से कम 1 प्रश्न पूछा गया था।
एक अनुपात समान प्रकार की दो या अधिक मात्राओं की तुलना करता है। यह दर्शाता है कि एक मात्रा दूसरी के सापेक्ष कितनी बड़ी है। सरल शब्दों में, दो मात्राओं का अनुपात हमें बताता है कि एक मात्रा दूसरी में कितनी बार फिट होती है। यदि हमारे पास दो मात्राएँ हैं, a और b, तो a का b के साथ अनुपात a/b के रूप में लिखा जाता है। इसका मतलब है कि दो मात्राओं का अनुपात एक मात्रा की तुलना में दूसरी मात्रा का भिन्न के समान है। इसलिए, जब हम a का b के साथ अनुपात कहते हैं, तो हम इसे a:b के रूप में लिखते हैं। अनुपात का पहला अंश पूर्ववर्ती कहलाता है, और दूसरा अंश उत्तरवर्ती कहलाता है। उदाहरण के लिए, 30 किलोग्राम और 50 किलोग्राम के बीच का अनुपात 3:5 के रूप में लिखा जाता है। यदि अनुपात के प्रत्येक अंश को समान संख्या से गुणा या विभाजित किया जाए, तो अनुपात वही रहता है। उदाहरण के लिए, अनुपात 4:3 अपरिवर्तित रहता है यदि दोनों अंशों को 10 से गुणा या विभाजित किया जाए, जिससे 40:30 प्राप्त होता है।
उदाहरण: एक कक्षा में कुल छात्रों की संख्या 95 है। यदि कक्षा में लड़कियों की कुल संख्या 45 है, तो लड़कों की कुल संख्या और लड़कियों की कुल संख्या का अनुपात क्या होगा: (क) 9 : 10 (ख) 7 : 8 (ग) 10 : 9 (घ) 9 : 11
समाधान: (ग) मान लेते हैं कि कक्षा में लड़कों की कुल संख्या 𝑥 है। प्रश्न के अनुसार:
𝑥 + 45 = 95
𝑥 = 95 - 45 = 50
इसलिए, लड़कों और लड़कियों की कुल संख्या का आवश्यक अनुपात है:
B: G = 50: 45 = 10: 9
अनुपात का वर्गीकरण: अनुपातों को निम्नलिखित प्रकारों में वर्गीकृत किया जाता है:
- डुप्लिकेट अनुपात: a:b का डुप्लिकेट अनुपात a²:b² है।
- उदाहरण: 6:11 का डुप्लिकेट अनुपात 36:121 है।
अनुपातों का वर्गीकरण
- डुप्लिकेट अनुपात: a:b का डुप्लिकेट अनुपात a²:b² है। उदाहरण: 6:11 का डुप्लिकेट अनुपात 36:121 है।
3. त्रैतीय अनुपात: a³:b³ को a:b का त्रैतीय अनुपात कहा जाता है। उदाहरण: 3:5 का त्रैतीय अनुपात 27:125 है।
4. उपडुप्लिकेट अनुपात: a:b का उपडुप्लिकेट अनुपात। उदाहरण: 25:36 का उपडुप्लिकेट अनुपात 5:6 है।
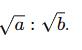
5. उपत्रैतीय अनुपात: a:b का उपत्रैतीय अनुपात कहा जाता है। उदाहरण: 216:343 का उपत्रैतीय अनुपात 6:7 है।
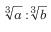
6. यौगिक अनुपात: ab:cd a:c और b:d का यौगिक अनुपात है। यह दो या अधिक दिए गए अनुपातों के पूर्ववर्ती के उत्पाद का अनुपात है।
7. प्रतिकूल अनुपात: 1/a:1/b a:b का प्रतिकूल अनुपात है। उदाहरण: 3:4 का प्रतिकूल अनुपात 1/3:1/4 या 4:3 है।
अनुपात केवल उन्हीं मात्राओं के बीच बनाया जा सकता है जिनकी एक ही इकाई होती है। उदाहरण के लिए, आप ₹64 और ₹96 की तुलना कर सकते हैं क्योंकि ये दोनों संख्याएँ हैं। हालाँकि, आप 64 (एक संख्या) और 96 किलोग्राम (एक वजन) के बीच अनुपात स्थापित नहीं कर सकते क्योंकि ये अलग-अलग प्रकार की मात्राएँ हैं।
उदाहरण: यदि 378 सिक्कों में ₹1, 50 पैसे, और 25 पैसे हैं, जिनका मूल्य 13:11:7 के अनुपात में है, तो 50 पैसे के सिक्कों की संख्या होगी: (a) 136 (b) 133 (c) 132 (d) 128
समाधान: (c) मान लीजिए कि ₹1, 50 पैसे, और 25 पैसे के सिक्कों के मूल्य क्रमशः 13x, 11x, और 7x हैं। चूंकि पैसे को रुपये में परिवर्तित करने के लिए 100 से विभाजित करना होता है, इसलिए 50 पैसे और 25 पैसे को 100 से विभाजित किया जाता है। इसलिए सिक्कों की संख्या = 22x6 = 132।
तीन से अधिक मात्राओं के बीच संबंध:
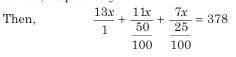
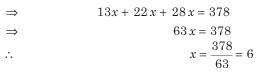
1. तीन मात्राओं के लिए: यदि A:B = x1:y1 और
2. चार मात्राओं के लिए: यदि A:B = N1:D1
उदाहरण: तीन संख्याओं का वर्ग का योग 532 है और पहली से दूसरी और दूसरी से तीसरी का अनुपात 3:2 है। दूसरी संख्या क्या है? (a) 2 (b) 6 (c) 12 (d) इनमें से कोई नहीं
समाधान: (c) मान लीजिए कि तीन संख्याएँ क्रमशः a, b और c हैं। तब a:b = 3:2 और b:c = 3:2 है। इसलिए, a:b:c = 3x3:2x3:2x2 = 9:6:4। इस प्रकार, a=9x, b=6x, c=4x (यहाँ, x सामान्य अनुपात है)।
दिए गए संख्या को दिए गए अनुपात में विभाजित करना
(क) यदि दो संख्याएँ अनुपात a1:a2 में हैं और इन संख्याओं का योग A है, तो ये संख्याएँ इस प्रकार होंगी:
यदि A L का मिश्रण है, जिसमें दो तरल P और Q अनुपात a1: a2 में हैं, तो मिश्रण में तरल P और Q की मात्रा क्रमशः इस प्रकार होगी। यदि तीन संख्याएँ अनुपात a1: a2: a3 में हैं और इन संख्याओं का योग A है, तो ये संख्याएँ क्रमशः इस प्रकार होंगी।
उदाहरण: यदि दो संख्याओं का अनुपात 20 : 39 है और उनका योग 295 है, तो ये संख्याएँ हैं (क) 100, 195 (ख) 150, 145 (ग) 105, 190 (घ) 110, 185। समाधान: (क) दूसरी संख्या। तो, दो संख्याएँ 100 और 195 हैं।
अनुपातों पर प्राथमिक सूत्र
सूत्र 1
यदि दो संख्याओं का अनुपात a : b है, तो इस अनुपात को c : d बनाने के लिए प्रत्येक संख्या से जो संख्या घटाई जानी चाहिए, वह इस प्रकार है:
उदाहरण: यदि दो संख्याओं का अनुपात 8 : 17 है, तो इस अनुपात को 2 : 5 बनाने के लिए क्या संख्या घटाई जानी चाहिए? (क) 2 (ख) 4 (ग) 5 (घ) 3। समाधान: (क) सूत्र के अनुसार, घटाई गई संख्या = यहाँ, a = 8, b = 17, c = 2 और d = 5।
सूत्र 2
यदि दो व्यक्तियों की आय का अनुपात a : b है और उनके व्यय का अनुपात c : d है और यदि प्रत्येक Rs. x बचाता है, तो उनकी आय और क्रमशः इस प्रकार हैं और उनके व्यय भी इस प्रकार हैं।
उदाहरण: रोहित और प्रताप की आय का अनुपात 4 : 3 है और उनके व्यय का अनुपात 3 : 2 है, यदि प्रत्येक Rs. 2500 बचाता है, तो उनकी आय क्या होगी? (क) Rs. 12000, Rs. 9000 (ख) Rs. 8000, Rs. 6000 (ग) Rs. 10000, Rs. 7500 (घ) इनमें से कोई नहीं। समाधान: (ग) मान लें कि रोहित और प्रताप की आय क्रमशः Rs. 4x और Rs. 3x है, एवं उनके व्यय Rs. 3y और Rs. 2y हैं। तो, प्रश्न के अनुसार, 4x − 3y = 2500 …(i) और 3x − 2y = 2500 …(ii)। समीकरणों (i) और (ii) को हल करने पर, हमें x = 2500 और y = 2500 मिलता है। ∴ रोहित की आय = 4 × x = 4 × 2500 = Rs. 10000 और प्रताप की आय = 3 × x = 3 × 2500 = Rs. 7500।
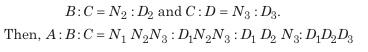
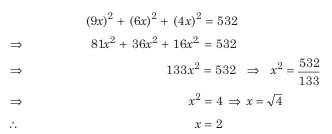
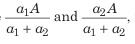
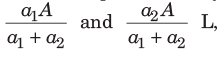
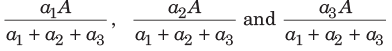
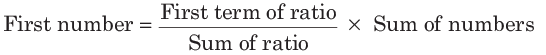
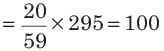
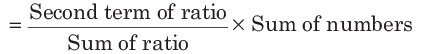
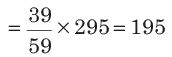
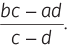
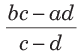
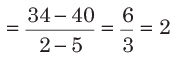
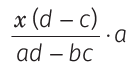
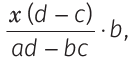
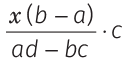
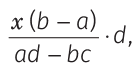
अनुपात
दो अनुपातों की समानता को अनुपात कहा जाता है। a, b, c और d को अनुपात में कहा जाता है, यदि a : b = c : d या a : b :: c : d। यहाँ, a पहला पद है, b दूसरा पद है, c तीसरा पद है और d चौथा पद है। पहले और चौथे पद को अत्यधिक कहा जाता है, अर्थात् a और d, जबकि दूसरे और तीसरे पद को मध्यम कहा जाता है, अर्थात् b और c। उदाहरण के लिए, यदि 3 : 2 :: 135 : 90, तो 3 और 90 को अत्यधिक कहा जाता है, जबकि 2 और 135 को मध्यम कहा जाता है।
एक अनुपात में, हमारे पास हमेशा होता है: अत्यधिक का गुणनफल = मध्यम का गुणनफल a:b::c:d ⇒ a × d = b × c
उदाहरण: ऐसे अंश को खोजें जो (a) (b) (c) (d) के समान अनुपात रखता हो। समाधान: (b) मान लें कि अंश x है। फिर, सूत्र के अनुसार ⇒ ∴
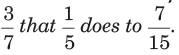
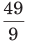
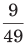
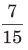
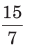
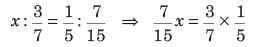
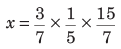
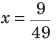
अनुपातों का वर्गीकरण अनुपात को तीन प्रकारों में वर्गीकृत किया जाता है:
- सतत अनुपात: यदि तीन मात्राएँ a, b और c इस प्रकार हैं कि a : b :: b : c, तो b = √(ac) और a, b और c सतत अनुपात में हैं। यहाँ, मात्रा c को a और b का तीसरा अनुपात कहा जाता है।
- माध्य अनुपात: यदि तीन मात्राएँ a, b और x इस प्रकार हैं कि a : x :: x : b, तो x = √(ab) और x को a और b का माध्य अनुपात कहा जाता है।
- चौथा अनुपात: यदि चार मात्राएँ a, b, c और x इस प्रकार हैं कि a : b :: c : x, तो ax = bc और x को a, b और c का चौथा अनुपात कहा जाता है।
- Invertendo: यदि a : b :: c : d, तो b : a :: d : c
- Alternendo: यदि a : b :: c : d, तो a : c = b : d
- Componendo: यदि a : b :: c : d, तो (a + b) : b :: (c + d) : d
- Dividendo: यदि a : b :: c : d, तो (a − b) : b :: (c − d) : d
- Componendo-dividendo: यदि a : b :: c : d, तो (a + b) : (a − b) :: (c + d) : (c − d)
उदाहरण: यदि 4, 6 और x सतत अनुपात में हैं, तो x का मान क्या है?
- (a) 14
- (b) 16
- (c) 9
- (d) 12
समाधान: (c). जब 4, 6 और x सतत अनुपात में होते हैं, तो इन्हें इस प्रकार लिखा जाता है: 4 : 6 :: 6 : x
∵ a : b :: b : c
अब, सतत अनुपात की शर्त लागू करते हुए:
b² = ac ⇒ (6)² = 4 × x ⇒ 36 = 4x
एकात्मक विधि
यह एक ऐसी विधि है जिसमें किसी मात्रा का मान पहले प्राप्त किया जाता है ताकि किसी आवश्यक मात्रा का मान ज्ञात किया जा सके।
एकात्मक विधि पर समस्याओं को हल करने के लिए दो प्रकार के अनुपात का उपयोग किया जाता है।
- प्रत्यक्ष अनुपात: दो मात्राएँ प्रत्यक्ष अनुपात में होती हैं, यदि इनमें से एक की मात्रा अनुपात में बढ़ती या घटती है, तो दूसरी भी उसी अनुपात में बढ़ती या घटती है। उदाहरण के लिए:
- (i) लेखों की संख्या अधिक हो, तो लागत भी अधिक होती है।
- (ii) श्रमिकों की संख्या अधिक हो, तो कार्य अधिक होता है।
- (iii) लेखों की संख्या कम हो, तो लागत भी कम होती है।
- (iv) श्रमिकों की संख्या कम हो, तो कार्य भी कम होता है।
- अप्रत्यक्ष अनुपात: दो मात्राएँ अप्रत्यक्ष अनुपात में होती हैं, यदि इनमें से एक की मात्रा अनुपात में बढ़ती या घटती है, तो दूसरी उसी अनुपात में घटती या बढ़ती है। उदाहरण के लिए:
- (i) श्रमिकों की संख्या अधिक हो, तो कार्य समाप्त करने के लिए आवश्यक दिन कम होते हैं।
- (ii) गति अधिक हो, तो किसी निश्चित दूरी को तय करने में समय कम लगता है।
- (iii) श्रमिकों की संख्या कम हो, तो कार्य समाप्त करने के लिए आवश्यक दिन अधिक होते हैं।
- (iv) गति कम हो, तो किसी निश्चित दूरी को तय करने में समय अधिक लगता है।
उदाहरण: यदि 15 अंडों की लागत ₹75 है, तो 5 दर्जन अंडों की लागत ज्ञात कीजिए।
- (a) ₹300
- (b) ₹400
- (c) ₹500
- (d) ₹600
हल:
15 अंडों की लागत = ₹75
1 अंडे की लागत =
अब, 5 दर्जन, अर्थात् 5 × 12 = 60 अंडों की लागत = 60 × 5 = ₹300
वैकल्पिक विधि: मान लीजिए 5 दर्जन (अर्थात् 5 × 12 = 60) अंडों की लागत = ₹x
तब, प्रत्यक्ष अनुपात का उपयोग करते हुए, अधिक अंडे, अधिक लागत:
15 : 75 :: 60 : x ⇒ ∴
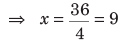
समाधान प्रश्न
प्रश्न 1: एक पुस्तकालय में, कहानी पुस्तकों की संख्या और गैर-कहानी पुस्तकों की संख्या का अनुपात 4:3 था और कुल कहानी पुस्तकों की संख्या 1248 थी। जब कुछ और कहानी पुस्तकें खरीदी गईं, तो अनुपात 5:3 हो गया। खरीदी गई कहानी पुस्तकों की संख्या ज्ञात करें।
उत्तर: विकल्प A स्पष्टीकरण:
प्रश्न 2: ₹8400 को A, B, C और D के बीच इस तरह बांटा गया है कि A और B, B और C, और C और D के हिस्से के अनुपात क्रमशः 2:3, 4:5, और 6:7 हैं। A का हिस्सा क्या है?
उत्तर: विकल्प A स्पष्टीकरण:
प्रश्न 3: पिता की वर्तमान आयु और पुत्र की आयु का अनुपात 7:2 है। 10 वर्षों बाद उनकी आयु का अनुपात 9:4 होगा। पिता की वर्तमान आयु क्या है?
उत्तर: विकल्प A
स्पष्टीकरण:
प्रश्न 4: अजयर और राज के पास मिलाकर ₹1050 हैं। यदि अजयर से ₹150 लिए जाएं, तो अजयर के पास वही राशि होगी जो राज के पास पहले थी। अजयर और राज के पास प्रारंभ में कितने पैसे थे?
उत्तर: विकल्प D स्पष्टीकरण:
प्रश्न 5: P, Q, और R प्रकार की प्रत्येक वस्तु की कीमत क्रमशः ₹300, ₹180 और ₹120 है। सुरेश प्रत्येक प्रकार की वस्तुओं को अनुपात 3:2:3 में ₹6480 में खरीदता है। उसने प्रकार Q की कितनी वस्तुएं खरीदीं?
क. 8
उत्तर: विकल्प A स्पष्टीकरण:
प्रश्न 6: ₹60 को माइक और जॉन के बीच 1:2 के अनुपात में बांटें। समाधान: मान लें कि माइक का हिस्सा x है।
तो जॉन का हिस्सा 2x है।
इस प्रकार, x + 2x = 60
3x = 60
x = (60/3)
x = 20।
इसलिए, माइक का हिस्सा = x = ₹20
जॉन का हिस्सा = 3x = ₹(2*20) = ₹40
प्रश्न 7: तीन बर्तन में शराब और पानी का अनुपात क्रमशः 3:5, 1:3, और 1:1 है। यदि सभी तीन समाधानों को मिलाया जाए, तो अंतिम समाधान में शराब और पानी का अनुपात क्या होगा?
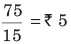
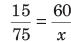
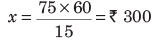





समाधान: यहाँ हमें तीन जार में समाधान की मात्राएँ नहीं दी गई हैं। केवल शराब और पानी के अनुपात का उल्लेख है। यदि समाधान की मात्रा का अनुपात दिया गया होता, तो हम अंतिम समाधान में शराब और पानी के अनुपात को निर्धारित कर सकते थे। इसलिए, यहाँ उत्तर होगा कि इसे निर्धारित नहीं किया जा सकता।
प्रश्न 8: यदि एक बैग में एक-रु्पये, 50 पैसे और 25 पैसे के सिक्कों के रूप में 495 रुपये हैं, जो 1:8:16 के अनुपात में हैं। तो बैग में कितने 50 पैसे के सिक्के हैं?
समाधान: मान लें, आपके पास x संख्या में एक रुपये के सिक्के हैं। अब सिक्के 1:8:16 के अनुपात में हैं। इसका मतलब है कि यदि हमारे पास x संख्या में एक रुपये के सिक्के हैं, तो हमारे पास 8x संख्या में 50 पैसे के सिक्के और 16x संख्या में 25 पैसे के सिक्के होंगे। यहाँ प्रश्न में अनुपात का जो क्रम दिया गया है, वह बहुत महत्वपूर्ण है। इस मामले में, क्रम है एक रुपये, 50 पैसे और 25 पैसे और अनुपात है 1:8:16। इसलिए,
50 पैसे के सिक्कों की संख्या = 8x
25 पैसे के सिक्कों की संख्या = 16x
अब, बैग में कुल पैसा = 495 रुपये
- x + (8x/2) + (16x/4) = 495
(50 पैसे के सिक्कों को रुपये में बदलने के लिए 2 से विभाजित किया गया और 25 पैसे के सिक्कों को रुपये में बदलने के लिए 4 से विभाजित किया गया)
- 9x = 495
- x = 495/9
- x = 55
इसलिए, 50 पैसे के सिक्कों की संख्या = 55 × 8 = 440
|
67 videos|98 docs|119 tests
|
















