अभ्यास प्रश्न: अनुपात और समानुपात | CSAT की तैयारी (हिंदी) - UPSC PDF Download

परिचय

यह दस्तावेज़ आपके संकल्पनात्मक सुदृढ़ीकरण के लिए एक अभ्यास सामग्री है। इस दस्तावेज़ का मुख्य उद्देश्य यह है कि आप अपने राष्ट्रीय परीक्षणों के प्रयास से पहले प्रश्नों का अभ्यास करें @EduRev ताकि आप उस परीक्षा में पूछे गए प्रश्नों से अधिक संबंधित हो सकें और अपने उत्तरों के प्रति अधिक आत्मविश्वास महसूस कर सकें। शुभकामनाएँ!

आसान स्तर

इस स्तर पर, प्रश्न आपके बुनियादी संकल्पनाओं के ज्ञान को सुधारने के लिए लक्षित हैं, हालांकि CAT में आसान प्रश्न दुर्लभ होते हैं। ये बुनियादी स्तर पर संकल्पनात्मक समझ के लिए अत्यंत महत्वपूर्ण हैं। पहले इस पिछले वर्ष के प्रश्न को स्वयं हल करने का प्रयास करें।

आसान स्तर

इस स्तर पर, प्रश्नों का उद्देश्य आपके बुनियादी अवधारणाओं के ज्ञान को बढ़ाना है, हालांकि आसान प्रश्न CAT में दुर्लभ होते हैं। ये नींव स्तर पर अवधारणात्मक समझ के लिए अत्यंत महत्वपूर्ण हैं। पहले इस पिछले वर्ष के प्रश्न को स्वयं हल करने का प्रयास करें।

प्रश्न उदाहरण 1: यदि तीन संख्याएँ 1 : 3 : 5 के अनुपात में हैं और आधी राशि 9 है, तो संख्याओं के घनों का अनुपात क्या होगा: (a) 6 : 12 : 13 (b) 1 : 3 : 25 (c) 1 : 27 : 125 (d) 3 : 5 : 7 उत्तर: (c) समाधान: 1 : 3 : 5 ► तो x, 3x और 5x का योग 18 है। ► तो संख्याएँ 2, 6 और 10 हैं। ► घनों का अनुपात = 8 : 216 : 1000 = 1 : 27 : 125।

प्रश्न उदाहरण 2: तीन मात्राएँ A, B, C इस प्रकार हैं कि AB = KC, जहाँ k एक स्थिरांक है। जब A स्थिर रहता है, तो B, C के अनुसार सीधा बदलता है; जब B स्थिर रहता है, तो A, C के अनुसार सीधा बदलता है और जब C स्थिर रहता है, तो A, B के अनुसार विपरीत रूप से बदलता है। प्रारंभ में, A 5 पर था और A : B : C 1 : 3 : 5 था। जब B 9 और C स्थिर है, तो A का मान ज्ञात करें। (a) 8 (b) 8.33 (c) 9 (d) 9.5 उत्तर: (b) समाधान: ► प्रारंभिक मान 5, 15 और 25 हैं। ► इस प्रकार, हमारे पास 5 * 15 = K * 25 है। ► इसलिए, K = 3। ► इस प्रकार, समीकरण AB = 3C है। ► समस्या के लिए, C को 25 पर स्थिर रखें। ► फिर, A * 9 = 3 * 25। अर्थात्, A = 75/9 = 8.33

प्रश्न उदाहरण 3: A ने ₹4,500 के साथ व्यवसाय शुरू किया और बाद में B ने ₹5,400 के साथ भाग लिया। यदि वर्ष के अंत में लाभ को 2 : 1 के अनुपात में विभाजित किया गया, तो B ने व्यवसाय में कब भाग लिया: (a) 5 महीने (b) 4 महीने (c) 6 महीने (d) 7 महीने उत्तर: (d) समाधान: ► लाभ साझा करने का अनुपात = 4500 × 12: 5400 × n जहाँ n वह अवधि है जिसके लिए B ने निवेश किया। ► अनुपात = 4500 × 12 : 5400 × n = 10 : n ► अब, यह अनुपात 2 : 1 के बराबर है ∴ 10 : n = 2 : 1 ⇒ n = 5 महीने ► इस प्रकार, B ने A के बाद 12 – 5 = 7 महीने में भाग लिया।

मध्यम स्तर

लगभग 70% प्रश्न CAT में मध्यम स्तर के प्रश्न होते हैं। हालांकि, अवधारणात्मक रूप से ये आसान लगते हैं, असली चुनौती है कि आप गणनाओं को तेजी से हल करें। हमने आपके लिए समस्याएँ तैयार की हैं ताकि आप समस्याओं को आसानी से हल कर सकें।

उदाहरण 1: X और Y की मासिक आय का अनुपात 1 : 3 है और उनके खर्चों का अनुपात 19 : 40 है। X की बचत Y से ₹18,860 कम है और कुल उनकी बचत ₹36,020 है। X और Y की आय क्रमशः क्या है: (a) ₹10,480 और ₹31,440 (b) ₹9,000 और ₹27,000 (c) ₹14,200 और ₹42,600 (d) ₹18,000 और ₹31,440 उत्तर: (a)

हल: मान लीजिए कि X की आय ₹p है और Y की आय ₹3p है। ► मान लीजिए कि X के खर्च ₹19q हैं और Y के खर्च ₹40q हैं। ► इसलिए, X की बचत = ₹(p – 19q) और Y की बचत = ₹(3p – 40q)। ► कुल बचत = (4p – 59q) = 36020 ► बचत का अंतर = (2p – 21q) = 18860 ► उपरोक्त समीकरणों को हल करते हुए, हमें p = 10480 मिलता है। ► इस प्रकार, X और Y की आय क्रमशः ₹10,480 और ₹31,440 है।

उदाहरण 2: एक छात्र ने पाँच विषयों में अंक 5 : 4 : 6 : 8 : 7 के अनुपात में प्राप्त किए हैं जिनकी अधिकतम अंक समान हैं। कुल मिलाकर, उसने सभी पाँच विषयों में अधिकतम अंक का 50% प्राप्त किया है। उसने कितने विषयों में अधिकतम अंक के 55% से अधिक अंक प्राप्त किए? (a) 1 (b) 2 (c) 3 (d) 4 उत्तर: (b)

हल: मान लीजिए कि उसके अंक क्रमशः 5x, 4x, 6x, 8x, और 7x हैं। ► प्राप्त कुल अंक = 30x = अधिकतम कुल अंकों का 50%। ► इस प्रकार, अधिकतम कुल अंक = 60x ► प्रति विषय अधिकतम अंक = 12 x 55% प्रति विषय अधिकतम अंक = 6.6x ► इसलिए, दो विषयों में अंक 6.6x से अधिक हैं।

उदाहरण 3: एक व्यक्ति बाजार से कुछ सेब और आम खरीदता है। एक आम की लागत कीमत एक सेब की लागत कीमत का दो गुना है और आम की बिक्री कीमत एक सेब की बिक्री कीमत का तीन गुना है। यदि वह एक सेब को उसकी लागत कीमत के दो गुने पर बेचता है, तो उसे कुल पर 150% लाभ होता है। बाजार से खरीदे गए आमों और सेबों की संख्या का अनुपात ज्ञात कीजिए। (क) 3 : 5 (ख) 3 : 4 (ग) 1 : 2 (घ) 2 : 3 उत्तर: (ग) समाधान: मान लीजिए कि व्यक्ति सेबों की संख्या A है और आमों की संख्या M है, तथा एक सेब की लागत कीमत Rs. x है। ► इसलिए, आम की लागत कीमत 2x होगी। ► कुल लागत कीमत = Ax + 2Mx। ► अब एक सेब की बिक्री कीमत 2x है। ∴ आम की बिक्री कीमत 6x होगी। ► कुल बिक्री कीमत = 2Ax + 6Mx। ► अब हमें 2Ax + 6Mx = 5(2Ax + 2Mx) या M/A = ½ प्राप्त होता है।

कठिन स्तर

इन प्रकार के प्रश्नों में से लगभग 25% प्रश्न CAT में आते हैं - यदि आपका लक्ष्य 95%ile से ऊपर है, तो हम सिफारिश करते हैं कि आप इन प्रश्नों को हल करें।

उदाहरण 1: एक पूर्ण बैरल में 729 लीटर शहद है, हम 'a' लीटर निकालते हैं और बैरल को पानी से भरते हैं। मिश्रण को अच्छी तरह से हिलाने के बाद, हम फिर से 'a' लीटर मिश्रण निकालते हैं और फिर से बैरल को पानी से भरते हैं। यह प्रक्रिया 6 बार दोहराने के बाद, बैरल में शहद की मात्रा 64 लीटर होती है। 'a' ज्ञात कीजिए। (क) 243 लीटर (ख) 81 लीटर (ग) 2.7 लीटर (घ) 3 लीटर

समाधान: ► निम्नलिखित विकल्पों में से प्रत्येक की जांच करें: मान लीजिए आप विकल्प (ख) की जांच कर रहे हैं, जो 'a' का मान 81 लीटर देती है। तब, यह स्पष्ट है कि जब आप 81 लीटर निकाल रहे हैं, तो आप बैरल में 8/9 शहद छोड़ रहे हैं। ► इस प्रकार, 6 ऐसी क्रियाओं के बाद बैरल में शहद की मात्रा होगी = 729 X (8/9)⁶। यदि यह उत्तर सही होना है, तो यह मान 64 के बराबर होना चाहिए (जो स्पष्ट रूप से नहीं है क्योंकि मान भिन्न के रूप में होगा)। ► इसलिए, यह सही विकल्प नहीं है। आप इसी तरह से अन्य विकल्पों को भी बाहर कर सकते हैं।

सोने, चांदी और पैलाडियम के दो मिश्र धातुएं हैं। पहली मिश्र धातु में 40 प्रतिशत पैलाडियम होता है और दूसरी मिश्र धातु में 26 प्रतिशत चांदी होती है। दोनों मिश्र धातुओं में सोने का प्रतिशत समान है। जब 150 किलोग्राम पहली मिश्र धातु और 250 किलोग्राम दूसरी मिश्र धातु को मिलाया जाता है, तो हमें एक नई मिश्र धातु मिलती है जिसमें सोने का प्रतिशत 30 है। नई मिश्र धातु में पैलाडियम की मात्रा कितनी किलोग्राम है? (क) 170 किलोग्राम (ख) 175 किलोग्राम (ग) 160 किलोग्राम (घ) 165 किलोग्राम उत्तर: (क)

हल: चूंकि दोनों मिश्र धातुओं में सोने का प्रतिशत समान है, इसलिए दोनों का कोई भी मिश्रण सोने का एक समान प्रतिशत सांद्रता रखेगा।

इसलिए, हमें मिलता है

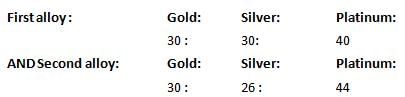
यह आपके अभ्यास दस्तावेज़ का अंत है, EduRev आपके ऑनलाइन अभ्यास परीक्षणों के लिए शुभकामनाएँ देता है।