सारांश: भिन्न (Fractions) | CSAT की तैयारी (हिंदी) - UPSC PDF Download
| Table of contents |

|
| CSAT में महत्व |

|
| भिन्न |

|
| भिन्नों के प्रकार |

|
| भिन्नों की तुलना |

|
| भिन्न का न्यूनतम रूप |

|
| समान भिन्नें |

|
| भिन्नों पर क्रियाएँ |

|
CSAT में महत्व
इस अध्याय से CSAT परीक्षा में सीधे प्रश्न अक्सर नहीं पूछे जाते हैं, लेकिन इसके संकल्पनाओं का उपयोग अन्य विषयों जैसे प्रतिशत, औसत, प्राथमिक बीजगणित आदि में किया जाता है। 2018 से 2023 के वर्षों में, इस अध्याय में उपयोग किए गए विभिन्न संकल्पनाओं जैसे दशमलव भिन्नों आदि के आधार पर प्रश्न पूछे गए हैं। इसलिए, एक छात्र को इस अध्याय के सभी संकल्पनाओं को स्पष्ट करना आवश्यक है।
एक भिन्न किसी पूरे का एक भाग है, चाहे वह कोई वस्तु, चीज़ या क्षेत्र हो। यह एक व्यक्ति की मूलभूत योग्यता का हिस्सा बनाता है, ताकि वह जनसंख्या, समूह या क्षेत्र के भागों का विचार कर सके।
भिन्न
वे सभी गणनात्मक संख्याएँ जो p/q के रूप में होती हैं, जहाँ p और q पूर्णांक होते हैं और p, q का गुणज नहीं होता, भिन्न कहलाते हैं। यहाँ, p को संख्याप्रधान और q को हर कहा जाता है। उदाहरण के लिए, यदि आप कहते हैं कि आपके पास आधी छड़ी है, तो इसका मतलब है कि यदि आप एक छड़ी को दो समान भागों में बाँटते हैं, तो आपके पास एक भाग होगा। इसका अर्थ है कि आपके पास छड़ी के 2 में से 1 भाग है। इसे 1/2 के रूप में व्यक्त किया जा सकता है। यह एक भिन्न कहलाता है।
भिन्नों के प्रकार
- सही भिन्नें: एक भिन्न जिसका अभсолют मूल्य 1 से कम है (अर्थात इसका संख्याप्रधान हर से कम है) को सही भिन्न कहा जाता है।
- गलत भिन्नें: जब हर, संख्याप्रधान से कम हो, तो उसे गलत भिन्न कहा जाता है।
- जटिल भिन्नें: ऐसे भिन्नों में संख्याप्रधान या हर दोनों भिन्न होते हैं।
- संयुक्त भिन्नें: यह भिन्नों का भिन्न है।
- व्युत्क्रम भिन्नें: यह दिए गए भिन्न का व्युत्क्रम होता है। उदाहरण: दिए गए भिन्न = 1/2 तो व्युत्क्रम भिन्न = 2/1।
- मिश्रित भिन्नें: यदि भिन्न में एक पूर्णांक और सही भिन्न एक साथ होते हैं, तो इसे मिश्रित भिन्न कहा जाता है।
- सतत भिन्नें: इसमें संख्याप्रधान या हर में एक अतिरिक्त भिन्न भाग होता है। जब हर में अतिरिक्त भिन्न भाग होता है, तो इसे सरल करने के लिए नीचे से शुरू करके ऊपर की ओर हल किया जाता है।
भिन्नों की तुलना
दो या अधिक भिन्नों की तुलना निम्नलिखित नियमों की मदद से की जा सकती है:
- नियम 1: जब दो भिन्नों का हर समान हो, तो बड़ी भिन्न वह होती है जिसका संख्याप्रधान बड़ा हो।
- नियम 2: जब दो भिन्नों का संख्याप्रधान समान हो, तो बड़ी भिन्न वह होती है जिसका हर छोटा हो।
- नियम 3: जब दो या अधिक भिन्नों की तुलना की जा रही हो जिनके हर और संख्याप्रधान भिन्न हैं, तो निम्नलिखित सरल तकनीक का उपयोग किया जाता है:
- चरण 1: मान लें कि संख्याप्रधान में अधिकतम अंकों की संख्या x है और हर में अधिकतम अंकों की संख्या y है।
- चरण 2: (y − x) ज्ञात करें। यदि (y − x) = 0 या 1 है, तो प्रत्येक भिन्न को 10 से गुणा करें और यदि (y − x) = 2, 3, 4 है, तो प्रत्येक भिन्न को क्रमशः 10², 10³, 10⁴ से गुणा करें।
- चरण 3: गुणा के बाद, केवल परिणामी भिन्न का पूर्णांक मान ज्ञात करें। यदि ऊपर दिए गए चरण से, कोई दो भिन्नों का समान पूर्णांक मान है, तो अगले दशमलव स्थान को ज्ञात करें और इसी तरह आगे बढ़ें।
- चरण 4: ऊपर के दो चरणों में प्राप्त पूर्णांक/दशमलव मानों की तुलना करें। जो भिन्न अधिकतम मान रखती है, वह सबसे बड़ी होती है।
उदाहरण: सबसे बड़ी भिन्न कौन सी है?
यहाँ, x = 3 (113, 303 और 144) और y = 3 (173, 486 और 231) है। ∴ (y − x) = 0। इसलिए, प्रत्येक भिन्न को 10 से गुणा करने पर हमें मिलते हैं। फिर, पूर्णांक मान ज्ञात करें और यदि पूर्णांक मान समान हैं, तो आगे बढ़ें और दशमलव मानों की तुलना करें, जो कि 6.11, 6.53, 6.234, 6.233 के बराबर है। ∴ सबसे बड़ी भिन्न = 113/173।
भिन्न का न्यूनतम रूप
संख्याप्रधान और हर को उनके HCF से विभाजित करके, हम भिन्न को उसके न्यूनतम रूप में प्राप्त करते हैं। उदाहरण: भिन्न 6/14 को न्यूनतम रूप में ज्ञात करने के लिए। चूंकि, 2 संख्याप्रधान (6) और हर (14) में HCF है, इसलिए दोनों को 2 से विभाजित करने पर हमें 3/7 प्राप्त होता है, जो 6/14 का न्यूनतम रूप है।
समान भिन्नें
यदि किसी भिन्न के संख्याप्रधान और हर को समान संख्या से गुणा किया जाता है, तो सभी परिणामी भिन्नों को समान भिन्नें कहा जाता है। सभी समान भिन्नें हैं लेकिन 1/2 न्यूनतम रूप है।
भिन्नों पर क्रियाएँ
भिन्नों पर क्रियाएँ निम्नलिखित रूप में वर्गीकृत की जा सकती हैं:
- भिन्नों का जोड़ और घटाव: यहाँ, दो मामले उत्पन्न होते हैं कि भिन्नों के हर समान हैं या नहीं।
- मामला 1: जब दो भिन्नों के हर समान होते हैं, तो हम हर को एक बार लिखते हैं और संख्याप्रधानों को जोड़ते (या घटाते) हैं।
- मामला 2: यदि हर भिन्न भिन्न हैं, तो हमें एक सामान्य हर ज्ञात करना होगा जो दोनों हरों में विभाजित होगा, यानी हमें हरों का LCM लेना होगा।
दशमलव भिन्नें
वे भिन्न जिनके हर 10 की शक्ति में होते हैं, उन्हें दशमलव भिन्न कहा जाता है। उदाहरण: 0.25 = शून्य दशमलव दो पाँच = एक चौथाई। 0.1 = शून्य दशमलव एक = एक-दशमलव। 13.489 में, 13 एक पूर्णांक भाग है जबकि 0.489 दशमलव भाग है।
किसी दशमलव को भिन्न में परिवर्तित करने की विधि
एक दशमलव भिन्न को परिवर्तित करने के लिए निम्नलिखित नियमों का पालन करें:
- (i) पहले अंक के नीचे दिए गए संख्या का हर 1 होना चाहिए।
- (ii) दशमलव बिंदु को हटाने के बाद, उसके बाद उतने शून्य रखें जितने दशमलव बिंदु के बाद के अंकों की संख्या है।
- (iii) अंत में, भिन्न को उसके न्यूनतम रूप में सरल करें।
दशमलव भिन्नों पर क्रियाएँ
दशमलव भिन्नों पर क्रियाएँ निम्नलिखित रूप में वर्गीकृत की जा सकती हैं:
- दशमलव भिन्नों का जोड़ या घटाव: दशमलव भिन्नों के जोड़ या घटाव में, हम दशमलव भिन्नों को इस प्रकार लिखते हैं कि सभी दशमलव बिंदु एक सीधी रेखा में हों, फिर इन संख्याओं को सरल तरीके से जोड़ा या घटाया जा सकता है।
- दशमलव भिन्नों का गुणा: 10 की शक्तियों से गुणा करने पर, दशमलव बिंदु को दाएँ जितनी जगहों पर ले जाया जाता है, उतनी संख्या में शून्य होते हैं।
उदाहरण: यदि करन, राजा, धर्मेश का 1 के एक योग में हिस्सा 0.68, 0.062 और 0.20 है, तो शेष हिस्सा दीपक का है।
समाप्त और न समाप्त होने वाले पुनरावृत्त दशमलव भिन्न
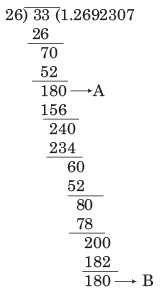
यदि किसी भिन्न का दशमलव अभिव्यक्ति समाप्त होता है, तो भिन्न को समाप्त भिन्न कहा जाता है। लेकिन, यदि हम उदाहरण लें 33 ÷ 26, तो इस विभाजन में, हम देखते हैं कि चरण A और B में शेष समान हैं। 26 द्वारा विभाजन की निरंतर प्रक्रिया में, अंश में 6, 9, 2, 3, 0, 7 की पुनरावृत्ति होती है। इसलिए, ऐसे दशमलव अभिव्यक्तियों को न समाप्त होने वाले पुनरावृत्त दशमलव कहा जाता है।
न समाप्त होने वाले, न पुनरावृत्त दशमलव भिन्न
हर भिन्न को समाप्त या न समाप्त होने वाले पुनरावृत्त दशमवों के रूप में लिखा जा सकता है, यानी ये दशमलव संख्याएँ p/q के रूप में रखी जा सकती हैं। इनको गणनात्मक संख्याएँ कहा जाता है लेकिन कुछ दशमलव संख्याएँ हैं जिन्हें p/q के रूप में नहीं रखा जा सकता, ये न समाप्त होने वाले, न पुनरावृत्त दशमलव होते हैं। इन्हें अगणित संख्याएँ कहा जाता है। उदाहरण: 0.101001000100001…
न समाप्त होने वाले पुनरावृत्त दशमलव को सरल भिन्न में परिवर्तित करने की विधि
पहले, न समाप्त होने वाले पुनरावृत्त दशमलव को बार नोटेशन में लिखें। फिर, संख्याप्रधान में पुनरावृत्त अंकों की संख्या के बराबर नाइन को हर में लिखें। संख्याप्रधान में दशमलव नहीं लगाना है।
उदाहरण: 0.33333... को सरल भिन्न में परिवर्तित करें। (a) 3/10 (b) 1/3 (c) 33/100 (d) 11/32
हल: (b) 0.3333… को 0.3 के रूप में लिखा जा सकता है। अब, इसे सरल भिन्न में परिवर्तित करने के लिए, हमें संख्याप्रधान में उतने ही 9 डालने होंगे जितने दशमलव में हैं। ∴ 1/3।
मिश्रित पुनरावृत्त दशमलव भिन्न
एक दशमलव भिन्न जिसमें कुछ अंक पुनरावृत्त नहीं होते हैं और कुछ पुनरावृत्त होते हैं, मिश्रित पुनरावृत्त दशमलव भिन्न कहलाते हैं। उदाहरण: 1.171734561818।
मिश्रित पुनरावृत्त दशमलव भिन्न को सरल भिन्न में परिवर्तित करने की विधि
पहले, पुनरावृत्त भाग को संख्या (बिना दशमलव) से घटाएँ और पुनरावृत्त अंकों की संख्या के बराबर नाइन डालें और साथ ही, गैर-पुनरावृत्त अंकों की संख्या के बराबर शून्य डालें।
उदाहरण: 3.0072 को सरल भिन्न में परिवर्तित करें। (a) (b) (c) (d)
हल:
CSAT में महत्व
इस अध्याय से अधिकांश समय सीधे प्रश्न CSAT परीक्षा में नहीं पूछे जाते हैं, लेकिन इसके सिद्धांत अन्य विषयों जैसे प्रतिशत, औसत, प्राथमिक बीजगणित और विभिन्न अन्य विषयों के साथ उपयोग किए जाते हैं। 2018 से 2023 के वर्षों में, विभिन्न सिद्धांतों जैसे दशमलव भिन्नों आदि पर आधारित प्रश्न पूछे गए हैं। इसलिए, एक छात्र को इस अध्याय के सभी सिद्धांतों को स्पष्ट करना चाहिए।
एक भिन्न किसी भी चीज़ का एक भाग होती है, चाहे वह एक वस्तु, चीज़ या क्षेत्र हो। यह किसी व्यक्ति की मूलभूत योग्यता का हिस्सा बनाती है, ताकि वह जनसंख्या, समूह या क्षेत्र के भागों का एक विचार रख सके।
भिन्न
सभी परिमेय संख्याएँ जो p/q के रूप में होती हैं, जहाँ p और q पूर्णांक हैं और p, q का गुणांक नहीं है, उन्हें भिन्न कहा जाता है। यहाँ, p को संख्यात्मक कहा जाता है जबकि q को हरात्मक कहा जाता है। उदाहरण के लिए, यदि आप आधे डंडे का संकेत देना चाहते हैं, तो कहा जा सकता है कि यदि आप एक डंडे को दो समान भागों में बाँटते हैं, तो आपके पास एक भाग होगा। इसका मतलब है कि आपके पास डंडे के 2 में से 1 भाग है। इसे 1/2 के रूप में दर्शाया जा सकता है। यह एक भिन्न है।
भिन्नों के प्रकार
- 1. सही भिन्नें: वह भिन्न जिसकी पूर्णांक मूल्य 1 से कम होती है (यानी, उनका संख्यात्मक हरात्मक से कम होता है)।
- 2. असही भिन्नें: जब हरात्मक संख्यात्मक से कम होता है, तो इसे असही भिन्न कहा जाता है।
- 3. जटिल भिन्नें: ऐसी भिन्नों में संख्यात्मक या हरात्मक या दोनों भिन्न होते हैं।
- 4. संयुक्त भिन्नें: यह भिन्नों का भिन्न होती है।
- 5. विपरीत भिन्नें: यह दी गई भिन्न का विपरीत होता है।
- 6. मिश्रित भिन्नें: यदि भिन्नों में एक पूर्णांक और सही भिन्नें मिलकर होती हैं, तो उन्हें मिश्रित भिन्नें कहा जाता है।
- 7. क्रमिक भिन्नें: इनमें संख्यात्मक या हरात्मक में एक अतिरिक्त भिन्न भाग होता है।
भिन्नों की तुलना
दो या दो से अधिक भिन्नों की तुलना निम्नलिखित नियमों की मदद से की जा सकती है:
- नियम 1: जब दो भिन्नों का हरात्मक समान हो, तो बड़ी भिन्न वह होती है जिसका संख्यात्मक बड़ा होता है।
- नियम 2: जब दो भिन्नों का संख्यात्मक समान हो, तो बड़ी भिन्न वह होती है जिसका हरात्मक छोटा होता है।
- नियम 3: जब दो या अधिक भिन्नों की तुलना की जाती है जिनके हरात्मक और संख्यात्मक भिन्न होते हैं, तो निम्नलिखित सरल तकनीक का उपयोग किया जाता है:
- चरण 1: मान लें कि संख्यात्मक में अधिकतम अंक की संख्या x है और हरात्मक में अधिकतम अंक की संख्या y है।
- चरण 2: (y − x) ज्ञात करें। यदि (y − x) = 0 या 1 है, तो प्रत्येक भिन्न को 10 से गुणा करें, और यदि (y − x) = 2, 3, 4 है, तो प्रत्येक भिन्न को क्रमशः 102, 103, 104 से गुणा करें।
- चरण 3: गुणा करने के बाद, केवल परिणामी भिन्न का पूर्णांक मान ज्ञात करें। यदि ऊपर दिए गए चरण से, किसी दो भिन्नों का समान पूर्णांक मान है, तो अगले दशमलव स्थान को ज्ञात करें और आगे बढ़ें।
- चरण 4: ऊपर दिए गए दो चरणों में प्राप्त पूर्णांक/दशमलव मान की तुलना करें। अधिकतम मान वाली भिन्न सबसे बड़ी होती है।
उदाहरण: सबसे बड़ी भिन्न कौन सी है? यहाँ, x = 3 (113, 303 और 144) और y = 3 (173, 486 और 231) है, ∴ (y − x) = 0। इसलिए, प्रत्येक भिन्न को 10 से गुणा करने पर हमें प्राप्त होता है। फिर, पूर्णांक मान ज्ञात करें और यदि पूर्णांक मान समान हैं, तो आगे बढ़ें और दशमलव मान की तुलना करें, जो 6.11, 6.53, 6.234, 6.233 के बराबर है। ∴ सबसे बड़ी भिन्न = 113/173।
भिन्न का न्यूनतम रूप
संख्यात्मक और हरात्मक को उनके महत्तम समापवर्तक द्वारा विभाजित करके, हम भिन्न को इसके न्यूनतम रूप में प्राप्त करते हैं। उदाहरण के लिए, भिन्न 6/14 को न्यूनतम रूप में ज्ञात करने के लिए, चूंकि 2 संख्यात्मक (6) और हरात्मक (14) में महत्तम समापवर्तक है, इसलिए दोनों को 2 से विभाजित करते हैं, हमें 3/7 प्राप्त होता है, जो 6/14 का न्यूनतम रूप है।
समान भिन्नें
यदि किसी भिन्न के संख्यात्मक और हरात्मक को समान संख्या से गुणा किया जाता है, तो सभी परिणामस्वरूप भिन्नों को समान भिन्न कहा जाता है। सभी समान भिन्नें हैं लेकिन 1/2 न्यूनतम रूप है।
भिन्नों पर क्रियाएँ
भिन्नों पर क्रियाएँ निम्नलिखित प्रकारों में वर्गीकृत की जा सकती हैं:
- 1. भिन्नों का जोड़ और घटाव: यहाँ, दो मामले उत्पन्न होते हैं कि भिन्नों के हरात्मक समान हैं या नहीं।
- 2. दशमलव भिन्न: उन भिन्नों को कहा जाता है जिनके हरात्मक का 10 की शक्ति है। उदाहरण के लिए, 0.25 = शून्य बिंदु दो पांच = एक चौथाई।
उदाहरण: यदि करण, राजा, धर्मेश का भाग 1 में 0.68, 0.062 और 0.20 है, तो दीपक का भाग दिया गया है।
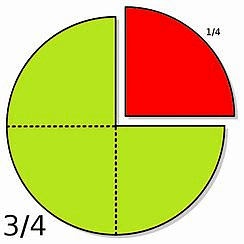
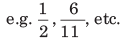
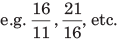
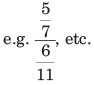
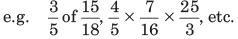
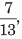
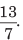
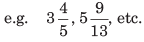
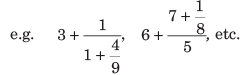
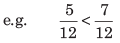
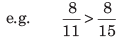
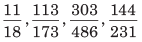
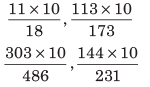
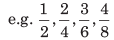
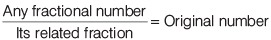
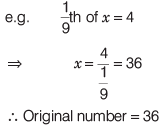
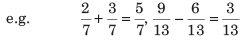
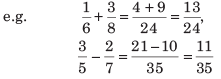
एक चौथाई 0.1 = शून्य दशमलव एक = एक-त्याहाई। 13.489 में, 13 एक पूर्णांक भाग है जबकि 0.489 दशमलव भाग है।
उदाहरण: यदि करण, राजा, और धर्मेश का हिस्सा 1 के एक योग में क्रमशः 0.68, 0.062 और 0.20 है, और शेष हिस्सा दीपक का है, तो दीपक का हिस्सा इस प्रकार दिया गया है: (क) 0.058 (ख) 0.048 (ग) 0.942 (घ) 0.0942।
हल: (क) मान लें दीपक का हिस्सा x है। फिर, करण, राजा, धर्मेश और दीपक के हिस्सों का योग = 1 ⇒ x + 0.68 + 0.062 + 0.20 = 1 ⇒ x + 0.942 = 1।
- ∴ x = 1 − 0.942 = 0.058
इसलिए, दीपक का हिस्सा 0.058 है।
2. दशमलव भिन्नों का गुणन:
10 की शक्तियों द्वारा गुणा करने के लिए, दशमलव बिंदु को दाईं ओर उतनी ही जगहों पर स्थानांतरित किया जाता है जितनी 10 की शक्ति में शून्य/शून्य हैं। उदाहरण: 0.75 × 10 = ?, 0.75 × 10 = 7.5 (दशमलव बिंदु को एक स्थान पर दाईं ओर स्थानांतरित किया गया है)।
10 के अलावा किसी अन्य संख्या से दशमलव का गुणा करने के लिए, हम दशमलव बिंदु की उपेक्षा करते हैं और साधारण तरीके से गुणा करते हैं और अंत में, दिए गए समस्या के अनुसार दाईं ओर से अंकों की संख्या के बाद दशमलव बिंदु रखते हैं।
यदि किसी भिन्न का दशमलव रूप समाप्त होता है, तो भिन्न को समाप्त कहा जाता है। जैसे, लेकिन यदि हम उदाहरण लेते हैं 33 ÷ 26, तो इस विभाजन में, हम देखते हैं कि चरण A और B में शेषफल समान हैं। 26 द्वारा विभाजन की निरंतर प्रक्रिया में, भागफल में अंकों 6, 9, 2, 3, 0, 7 की पुनरावृत्ति होगी। यह विभाजन की प्रक्रिया निरंतर है। इसलिए, ऐसे दशमलव रूपों को निरंतर पुनरावृत्त (दोहराने वाले) दशमलव कहा जाता है। दोहराते अंकों पर, हम रखते हैं।
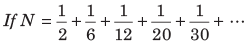

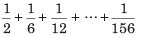
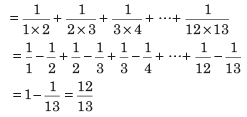
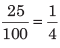
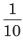
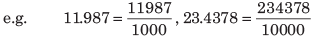
हर भिन्न को समाप्त या गैर-समाप्त आवर्ती दशमलव के रूप में लिखा जा सकता है, अर्थात् ये दशमलव संख्याएँ p / q के रूप में व्यक्त की जा सकती हैं। इन्हें गणितीय संख्याएँ कहा जाता है, लेकिन कुछ दशमलव संख्याएँ हैं जिन्हें p / q के रूप में नहीं लिखा जा सकता, ये गैर-समाप्त, गैर-आवर्ती दशमलव हैं। इन्हें असंगत संख्याएँ भी कहा जाता है। जैसे: 0.101001000100001…
उदाहरण: 0.33333... को साधारण भिन्न में परिवर्तित करें। (क) 3/10 (ख) 1/3 (ग) 33/100 (घ) 11/32 हल: (ख) 0.3333… को 0.3 के रूप में लिखा जा सकता है। अब, इसे साधारण भिन्न में बदलने के लिए, हम भिन्न के हर दशमलव के लिए जितने 9 डालते हैं, उतने ही 9 हर में डालेंगे। ∴
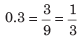
उदाहरण: 3.0072 को साधारण भिन्न में परिवर्तित करें। (क) (ख) (ग) (घ) हल:
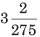
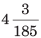
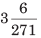
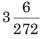
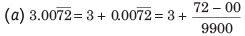
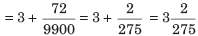
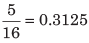
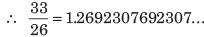
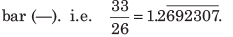
|
67 videos|98 docs|119 tests
|














