संक्षेप: द्विघात समीकरण | CSAT की तैयारी (हिंदी) - UPSC PDF Download

CSAT कोण

CSAT के दृष्टिकोण से और पिछले वर्षों के प्रश्न पत्रों के विश्लेषण के अनुसार, यह ध्यान में आया है कि वर्ष 2023 में इस अध्याय से दो प्रश्न और वर्ष 2022-2016 में प्रत्येक वर्ष एक प्रश्न पूछा गया था।

‘प्राथमिक बीजगणित’ विषय CSAT परीक्षा के लिए बहुत महत्वपूर्ण है, न केवल सीधे प्रश्न जैसे कि एक समीकरण को हल करना, दिए गए समीकरण के आधार पर कुछ घटकों का मान खोजना पूछा जाता है, बल्कि रेखीय समीकरण/द्विघात समीकरण के निर्माण की मूल अवधारणाएँ औसत, मापन और प्रतिशत जैसे विषयों में उपयोगी होती हैं। पॉलीनोमियल एक ग्रीक शब्द है जो ‘Poly’ अर्थात ‘कई’ और ‘Nomial’ अर्थात ‘शर्तें’ से मिलकर बना है, इसलिए एक पॉलीनोमियल कई शर्तों का एक साथ एक अभिव्यक्ति या समीकरण के रूप में संयोजन है।

एक अभिव्यक्ति के रूप में: f(x) = a0 + a1x + a2x² + ... + anxⁿ जहाँ a0, a1, a2, ..., an स्थिरांक (वास्तविक संख्या) हैं, an ≠ 0 है, और n एक गैर-ऋणात्मक पूर्णांक है, इसे वास्तविक संख्याओं के संदर्भ में x के लिए एक पॉलीनोमियल कहा जाता है। वास्तविक संख्याएँ a0, a1, a2, ..., an पॉलीनोमियल के गुणांक कहलाती हैं। यदि a0, a1, a2, ..., an सभी पूर्णांक हैं, तो इसे पूर्णांक के संदर्भ में पॉलीनोमियल कहा जाता है। यदि वे रैशनल नंबर हैं, तो इसे रैशनल के संदर्भ में पॉलीनोमियल कहा जाता है। उदाहरण के लिए: (i) 4x² + 7x - 9 एक पूर्णांक के संदर्भ में पॉलीनोमियल है। (ii) 7/3x³ - 2/3x² - 7/3x + 5 एक रैशनल के संदर्भ में पॉलीनोमियल है। (iii) 4x² - √3x + √5 एक वास्तविक संख्याओं के संदर्भ में पॉलीनोमियल है। पॉलीनोमियल से संबंधित कुछ महत्वपूर्ण शर्तें इस प्रकार हैं:

• मोनोमियल: एक पॉलीनोमियल जिसमें केवल एक शर्त होती है, उसे मोनोमियल कहा जाता है। उदाहरण: 7, 2x और 8x³ मोनोमियल हैं।
• बाइनोमियल: एक पॉलीनोमियल जिसमें दो शर्तें होती हैं, उसे बाइनोमियल कहा जाता है। उदाहरण: 3x + 4, 8x² - 3x और x² + 8 बाइनोमियल हैं।
• ट्रिनोमियल: एक पॉलीनोमियल जिसमें तीन शर्तें होती हैं, उसे ट्रिनोमियल कहा जाता है। उदाहरण: 7x² - 3x + 8 एक ट्रिनोमियल है।

बहुपद का डिग्री

एक बहुपद में सबसे उच्च डिग्री के पद का घातांक, उसके डिग्री के रूप में जाना जाता है।

बहुपद के प्रकार

नीचे दिए गए पांच प्रकार के बहुपद हैं:

• शून्य बहुपद एक शून्य डिग्री का बहुपद कहलाता है। उदाहरण के लिए, f(x) = 8, f(x) = -5/2। शून्य बहुपद की डिग्री निर्धारित नहीं होती।
• रेखीय बहुपद एक एकल डिग्री का बहुपद कहलाता है। सामान्यतः, f(x) = ax + b, जहाँ a ≠ 0 होता है। उदाहरण के लिए, f(x) = 3x − 7 एक रेखीय बहुपद है क्योंकि x की सबसे उच्च डिग्री 1 है।
• गुणात्मक बहुपद एक दो डिग्री का बहुपद कहलाता है। सामान्यतः, f(x) = ax² + bx + c, जहाँ a ≠ 0 होता है। उदाहरण के लिए, f(x) = x² − 7x + 8 एक गुणात्मक बहुपद है क्योंकि x की सबसे उच्च डिग्री 2 है।
• घन बहुपद एक तीन डिग्री का बहुपद कहलाता है। सामान्यतः, f(x) = ax³ + bx² + cx + d, जहाँ a ≠ 0 होता है। उदाहरण के लिए, f(x) = 2x³ − x² + 8x − 4 एक घन बहुपद है क्योंकि x की सबसे उच्च डिग्री 3 है।
• बिक्वाड्रेटिक बहुपद एक चार डिग्री का बहुपद कहलाता है। सामान्यतः, f(x) = ax⁴ + bx³ + cx² + dx + e, जहाँ a ≠ 0 होता है। उदाहरण के लिए, f(x) = 4x⁴ + 3x³ + 9x² + 5x + 2 = 0 एक बिक्वाड्रेटिक बहुपद है क्योंकि x की सबसे उच्च डिग्री 4 है।

एक बहुपद का शून्य

यदि एक वास्तविक संख्या α एक बहुपद f(x) का शून्य (या मूल) है, तो f(α) = 0। उदाहरण के लिए, यदि x = 1 बहुपद 3x³ − 2x² + x − 2 का मूल है, तो f(1) = 0। हम जानते हैं, f(x) = 3x³ − 2x² + x − 2, अतः f(1) = 3 × 1³ − 2 × 1² + 1 − 2 = 3 − 2 + 1 − 2 = 0। इसलिए, x = 1 बहुपद f(x) का मूल है।

पोलिनोमियल की डिग्री n तक अधिकतम n जड़ें होती हैं। एक रैखिक पोलिनोमियल f(x) = ax + b, जहाँ a ≠ 0, का एक अद्वितीय मूल होता है जिसे x = -b/a द्वारा दिया जाता है। हर वास्तविक संख्या शून्य पोलिनोमियल की जड़ होती है। एक गैर-शून्य स्थिर पोलिनोमियल की कोई जड़ नहीं होती।

• एक रैखिक पोलिनोमियल f(x) = ax + b, जहाँ a ≠ 0, का एक अद्वितीय मूल होता है जिसे x = -b/a द्वारा दिया जाता है।

उदाहरण: नीचे दिए गए पोलिनोमियल के प्रकार खोजें (डिग्री के आधार पर)। (i) 3x² + 4x + 5 (ii) 3 + 3z + 4z⁴ हल: (i) यहाँ, दिए गए पोलिनोमियल में x की सबसे बड़ी शक्ति 2 है। इसलिए, यह एक द्विघात पोलिनोमियल है। (ii) यहाँ, दिए गए पोलिनोमियल में z की सबसे बड़ी शक्ति 4 है। इसलिए, यह एक बिक्वाड्रेटिक पोलिनोमियल है।

शेष प्रमेय

मान लीजिए f(x) एक पोलिनोमियल है जिसकी डिग्री एक या उससे अधिक है और a कोई वास्तविक संख्या है। यदि f(x) को (x - a) से विभाजित किया जाता है, तो शेष f(a) के बराबर होता है। उदाहरण: जब f(x) = 2x³ − 13x² + 17x − 10 को (x − 2) से विभाजित किया जाता है, तो शेष ज्ञात करें। (a) 8 (b) 9 (c) 10 (d) 12 हल: (a) जब f(x) को (x − 2) से विभाजित किया जाता है, तो शेष f(2) द्वारा दिया जाता है: f(2) = 2(2)³ - 13(2)² + 17(2) - 10 = 16 - 52 + 34 - 10 = 8 इस प्रकार, f(x) = 2x³ − 13x² + 17x − 10 को x − 2 से विभाजित करने पर शेष 8 के बराबर है।

गुणन प्रमेय

मान लीजिए f(x) एक पोलिनोमियल है जिसकी डिग्री एक या उससे अधिक है और a कोई वास्तविक संख्या है जिससे f(a) = 0 हो, तो (x − a) f(x) का एक गुणक है। इसके विपरीत, यदि (x − a) f(x) का एक गुणक है, तो f(a) = 0 होता है। उदाहरण: दिखाएँ कि (x + 2) x² + 4x + 4 का एक गुणक है। हल: मान लीजिए f(x) = x² + 4x + 4, तब (x + 2) = {x − (−2)} f(x) का एक गुणक है, यदि f(−2) = 0 हो। ∴ f(−2) = (−2)² + 4(−2) + 4 = 4 - 8 + 4 = 0 इसलिए, (x + 2) f(x) का एक गुणक है।

महत्वपूर्ण सूत्र

• (x y)² = x² y² + 2xy
• (x − y)² = x² + y² − 2xy
• (x² − y²) = (x + y)(x − y)
• (x y z)² = x² y² z² + 2(xy + yz + zx)
• (x y)² (x − y)² = 2(x² y²)
• (x y)² − (x − y)² = 4xy
• (x y)³ = x³ y³ + 3xy (x y)
• (x³ − y³) = (x − y)(x² + y² + xy)
• (x³ y³) = (x y)(x² + y² − xy)
• (x³ y³ z³ − 3xyz) = (x y z)(x² y² z² − xy − yz − zx)
• यदि x y z = 0, तो x³ y³ z³ = 3xyz

रेखीय समीकरण

जब हम दो बीजगणितीय अभिव्यक्तियों को समानता के चिह्न का उपयोग करके समान करते हैं, तो यह एक समीकरण बनाता है। एक रेखीय समीकरण एक बीजगणितीय समीकरण है जिसमें प्रत्येक पद या तो एक स्थिरांक होता है या एक स्थिरांक और एक एकल चर का गुणनफल होता है। रेखीय समीकरण पहले दर्जे के समीकरण होते हैं और इनमें एक या अधिक चर हो सकते हैं। यदि समीकरण में केवल एक चर है, तो समीकरण स्वयं ही उस चर का मान प्राप्त करने के लिए पर्याप्त है, और यदि समीकरण में दो चर हैं, तो चरों का मान प्राप्त करने के लिए दो संगत समीकरणों की आवश्यकता होती है। सामान्यतः, यदि एक समीकरण में n चर हैं, तो n संगत समीकरणों की आवश्यकता होती है ताकि सभी n चरों के मान प्राप्त किए जा सकें।

एक चर में रैखिक समीकरण

ये पहले दर्जे के समीकरण हैं जिनमें एक अज्ञात चर होता है। समीकरण जो इस रूप में होता है ax + b = 0, जहां a, b ∈ R और a ≠ 0 है, उसे एक चर में रैखिक समीकरण कहा जाता है। इसमें केवल एक चर x है, जिसका मान ज्ञात करना है। उदाहरण के लिए, (x + 5) = 0 और (y − 7) = 0 एक चर में रैखिक समीकरण हैं, जिसमें हमें समीकरण के आधार पर x या y का मान ज्ञात करना है। उदाहरण: सत्यापित करें कि x = 2 रैखिक समीकरण 2x + 7 = 13 − x का समाधान है। हल: दिए गए रैखिक समीकरण को देखते हैं: 2x + 7 = 13 − x। x = 2 को समीकरण में प्रतिस्थापित करने पर, हमें मिलता है: LHS = 2 × 2 + 7 = 4 + 7 = 11, RHS = 13 − 2 = 11। अतः, LHS = RHS। इसलिए, x = 2 समीकरण का समाधान है।

दो चर में रैखिक समीकरण

ये पहले दर्जे के समीकरण हैं जिनमें दो अज्ञात चर होते हैं। समीकरण जो इस रूप में होता है ax + by + c = 0, जहां a, b, c ∈ R, a ≠ 0 और b ≠ 0 है, उसे दो चर में रैखिक समीकरण कहा जाता है। इसमें दो चर x और y हैं, जिनका मान ज्ञात करना है। x और y के किसी भी जोड़ी मान, जो समीकरण ax + by + c = 0 को संतुष्ट करते हैं, को उसका समाधान कहा जाता है। जब दो या अधिक समीकरणों को एक ही सेट के मान द्वारा संतुष्ट किया जाता है, तो उन्हें समकालिक समीकरण कहा जाता है।

दो समकालिक रैखिक समीकरणों को हल करने के तरीके

दो रैखिक समीकरणों को हल करने के तरीके निम्नलिखित हैं:

प्रतिस्थापन की विधि

• चरण 1: एक चर (मान लीजिए y) का मान दूसरे चर x के संदर्भ में ज्ञात करें, जो किसी भी समीकरण से लिया जा सकता है।
• चरण 2: प्राप्त y के मान को दूसरे समीकरण में प्रतिस्थापित करें। इस प्रकार, हमें एक चर x में एक समीकरण प्राप्त होता है।
• चरण 3: इस समीकरण को x के लिए हल करें।
• चरण 4: चरण 1 में प्राप्त x के मान को प्रतिस्थापित करें और y का मान ज्ञात करें।

उदाहरण: समीकरण x + y = 7, 3x − 2y = 11 को हल करें और फिर x और y के मान ज्ञात करें। (a) x = 5, y = 2 (b) x = 2, y = 5 (c) x = 3, y = 1 (d) x = −1, y = 3 हल: (a) दिए गए समीकरण हैं x + y = 7 …(i) और 3x − 2y = 11 …(ii) समीकरण (i) से, y = (7 − x)। समीकरण (ii) में y = (7 − x) को प्रतिस्थापित करने पर, हमें मिलता है: 3x − 2(7 – x) = 11 ⇒ 3x − 14 + 2x = 11 ⇒ 5x = 25 ⇒ x = 5। समीकरण (i) में x के मान को प्रतिस्थापित करने पर, हमें मिलता है: 5 + y = 7 अतः, y = 7 − 5 = 2। इसलिए, x = 5 और y = 2 आवश्यक समाधान है।

समाधान की विधि

• चरण 1: दो समीकरण प्राप्त करें।
• चरण 2: समीकरण को इस प्रकार गुणा करें कि विलोपित होने वाले चर का गुणांक समान हो जाए।
• चरण 3: चरण 2 में प्राप्त समीकरणों को जोड़ें या घटाएं, यह इस आधार पर कि समान गुणांक वाले पद विपरीत या समान चिह्न के हैं।
• चरण 4: चरण 3 में प्राप्त एक चर का समीकरण हल करें।
• चरण 5: चरण 4 में प्राप्त मान को किसी एक समीकरण में प्रतिस्थापित करें और दूसरे चर का मान खोजें।
• चरण 6: चरण 4 और 5 में प्राप्त चर के मान समाधानों का गठन करते हैं।

दो रेखीय समीकरणों को हल करने की शॉर्टकट विधि (क्रॉस-मल्टीप्लिकेशन विधि)

मान लें कि दो समीकरण हैं a₁x + b₁y = c₁ और a₂x + b₂y = c₂। तब, समाधान को इस प्रकार लिखा जाता है:

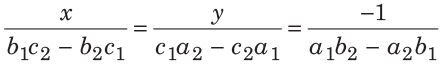
यानी, समाधानशीलता के आधार पर रेखीय समीकरणों के प्रकार:

• (i) संगत समीकरणों का प्रणाली: एक रेखीय समीकरणों का प्रणाली संगत कहा जाता है, यदि इसका एक समाधान है।
• (ii) असंगत समीकरणों का प्रणाली: एक रेखीय समीकरणों का प्रणाली असंगत कहा जाता है, यदि इसका कोई समाधान नहीं है।

समीकरणों के एक प्रणाली की संगति

समीकरणों की प्रणाली पर विचार करें: a1x + b1y + c1 = 0 और a2x + b2y + c2 = 0

• यदि a1/b2 ≠ b1/b2, तो एक अद्वितीय समाधान है।
• यदि …, तो अनंत संख्या में समाधान हैं।
• यदि …, तो कोई समाधान नहीं है।

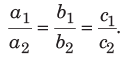
उदाहरण: समीकरणों को हल करें: x + 2y = 7, x − y = 1 और फिर x और y के मान ज्ञात करें।

• (a) 5, 4
• (b) 1, 4
• (c) 3, 2
• (d) 3, 3

हल: (c) रैखिक समीकरण हल करने की शॉर्टकट विधि का उपयोग करते हुए, यहाँ, a1 = 1, b1 = 2, c1 = 7 और a2 = 1, b2 = −1, c2 = 1 है।

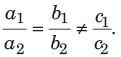
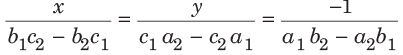
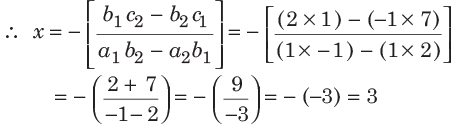
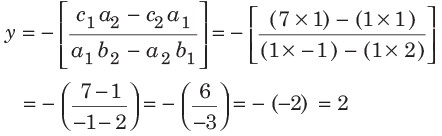
इसलिए, x = 3 और y = 2 आवश्यक समाधान है।

द्विघात समीकरण

• (i) x² + 5x + 6 = 0 की जड़ें हैं: x = −2, −3।
• (ii) 15x² − x − 28 = 0 की जड़ें हैं: x = 7/5, -4/3।
• (iii) x² − 8 = 0 की जड़ें हैं: x = 2√2, -2√2।

द्विघात समीकरणों की जड़ों को खोजने की विधि

सामान्यतः, द्विघात समीकरण की जड़ें निम्नलिखित विधि द्वारा ज्ञात की जा सकती हैं:

• 1. गुणनखंडन द्वारा: यदि द्विघात समीकरण ax² + bx + c = 0 को इस रूप में व्यक्त किया जा सके: (x − α)(x − β) = 0, तो समीकरण की जड़ें α और β हैं।

उदाहरण: समीकरण x² − 10x + 24 = 0 की संभावित जड़ों के मान ज्ञात करें।

• (a) 4, 4
• (b) 6, 4
• (c) 6, 6
• (d) 7, 6

हल: (b) हमारे पास है:

x² − 10x + 24 = 0 ⇒ x² − 6x − 4x + 24 = 0 ⇒ x(x − 6) − 4(x − 6) = 0 ⇒ (x − 6)(x − 4) = 0 ⇒ (x − 6) = 0 या (x − 4) = 0 ⟹ x = 6 या 4।

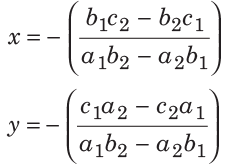
2. सीधे सूत्र का उपयोग यदि द्विघात समीकरण ax² + bx + c = 0 है, तो हम समीकरण की जड़ों को खोजने के लिए नीचे दिए गए मानक सूत्र, जिसे द्विघात सूत्र कहा जाता है, का उपयोग कर सकते हैं। यदि α और β द्विघात समीकरण की जड़ें हैं, तो

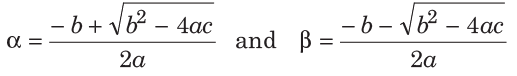
इसके अलावा, b² − 4ac = D (अवकलन)

• हमारे पास है, अवकलन, D = b² − 4ac।
  • (i) यदि D < 0="" है,="" तो="" जड़ें="" α="" और="" β="" काल्पनिक="" हैं।="" />
  • (ii) यदि D > 0 है, तो जड़ें α और β वास्तविक और भिन्न हैं।
  • (iii) यदि D = 0 है, तो जड़ें α और β वास्तविक और समान हैं।
  • यदि D एक पूर्ण वर्ग है, तो जड़ें समानुपातिक संख्याएँ हैं।
  • यदि D सकारात्मक है लेकिन एक पूर्ण वर्ग नहीं है, तो जड़ें असमानुपातिक संख्याएँ हैं जिसमें एक अंश है।

द्विघात समीकरण के गुणांक और जड़ों के बीच संबंध

मान लीजिए ax² + bx + c = 0 एक द्विघात समीकरण है और α, β जड़ें हैं। तब, जड़ों का योग और जड़ों का गुणनफल,

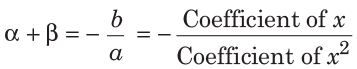
यदि द्विघात समीकरण की जड़ों का योग = (α + β) और द्विघात समीकरण का जड़ों का गुणनफल = αβ है, तो द्विघात समीकरण के पद हैं x² − (α + β)x + αβ = 0, यानि x² − (जड़ों का योग)x + जड़ों का गुणनफल = 0।

• (i) यदि a = c है, तो जड़ें एक-दूसरे के व्युत्क्रम हैं।
• (ii) यदि c = 0 है, तो एक जड़ शून्य है।
• (iii) यदि c = −a है, तो जड़ें एक-दूसरे के नकारात्मक व्युत्क्रम हैं।
• (iv) यदि b = 0 और c = 0 है, तो दोनों जड़ें शून्य के बराबर हैं।
• (v) यदि a और c के संकेत विपरीत हैं, तो जड़ें विपरीत संकेत की होनी चाहिए।
• (vi) यदि b = 0 है, तो जड़ें एक-दूसरे के नकारात्मक हैं।

उदाहरण हल किया गया

उदाहरण 1: निम्नलिखित बहुपद p (x) = x³ + 2x - 6/x का डिग्री क्या है? (a) 2 (b) 4 (c) 3 (d) 5 उत्तर: (b) हल: इसलिए, बहुपद का डिग्री सबसे उच्च घातांक डिग्री का पद है, अर्थात 4।

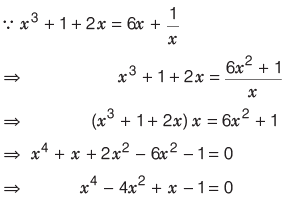
उदाहरण 2: रमेश और गणेश के पास प्रारंभ में कुछ संतरे थे। यदि रमेश ने गणेश को 5 संतरे दिए, तो गणेश के पास रमेश की तुलना में तीन गुना अधिक संतरे होंगे। इसके बजाय, यदि गणेश ने रमेश को 5 संतरे दिए, तो दोनों के पास समान संख्या में संतरे होंगे। रमेश और गणेश के बीच वितरित संतरों का अनुपात ज्ञात करें। (a) 3 : 5 (b) 1 : 3 (c) 5 : 7 (d) 7 : 9 उत्तर: (a) मान लें कि रमेश के पास संतरे की संख्या x है और गणेश के पास संतरे की संख्या y है। फिर, पहले शर्त के अनुसार, y + 5 = 3 (x - 5) ⇒ 3x - y - 20 = 0 ...(i) दूसरी शर्त के अनुसार, x + 5 = y - 5 ⇒ x - y + 10 = 0 …(ii) समीकरण (ii) को समीकरण (i) से घटाने पर हमें मिलता है 2x - 30 = 0 ⇒ x = 15। समीकरण (ii) में x का मान लगाने पर हमें मिलता है y = 25। अतः रमेश और गणेश के बीच वितरित संतरों का अनुपात = 15 : 25 = 3 : 5