द्विघात समीकरण: अभ्यास प्रश्न | CSAT की तैयारी (हिंदी) - UPSC PDF Download

प्रश्न 1: यदि (p – x)(p – y) = 1 और (x – y = √5), तो, (a) 4√5 (b) 8√5 (c) 6√7 (d) 10√5 का मान क्या है?

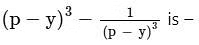
उत्तर: (b) समाधान: दिए गए: (p – x)(p – y) = 1 इसके अलावा, (x - y)=√5 उपयोग की गई सूत्र: (x – y)³ = x³ – y³ – 3xy(x – y) गणना: (p – x)(p – y) = 1

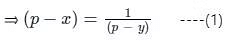
⇒ x - y = √5 ----(2) 'p' को समीकरण (2) के बाईं ओर जोड़ें और घटाएं

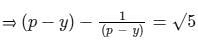
दोनों तरफ घन लेते हुए, हमें मिलता है –

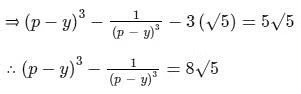
प्रश्न 2: बहुपद 6x² + 3x² – 5x + 1 के शून्य के व्युत्क्रम का योग क्या है? (a) 2 (b) 3 (c) 4 (d) 5

उत्तर: (d) समाधान: दिए गए: 6x² + 3x² – 5x + 1 गणना: 6x² + 3x² – 5x + 1 ⇒ 9x² – 5x + 1 मान लें 'a' और 'b' समीकरणों की दो जड़ें हैं। जैसे कि हम जानते हैं, जड़ों का योग (α + β) = (-b)/a = 5/9 और जड़ों का गुणनफल (αβ) = c/a = 1/9। प्रश्न के अनुसार ⇒ 1/α + 1/β ⇒ (α + β)/αβ ⇒ [5/9] / [1/9] = 5

प्रश्न 3: समीकरण x² – 12x + k = 0 में से एक जड़ x = 3 है। दूसरी जड़ है: (a) x = -4 (b) x = 9 (c) x = 4 (d) x = -9

उत्तर: (b) समाधान: संकल्पना: द्विघात समीकरण की जड़ें समीकरण को संतुष्ट करती हैं, इसलिए एक जड़ के मान को रखकर, एक अज्ञात चर का मान और इस प्रकार दूसरी जड़ ज्ञात की जा सकती है। गणना: हम समीकरण x² – 12x + k = 0 में x = 3 का मान रखते हैं, ⇒ 9 – 36 + k = 0 ⇒ k = 27। समीकरण में k का मान रखते हुए, हमें मिलता है: x² – 12x + 27 = 0 ⇒ x² – 9x – 3x + 27 = 0 ⇒ x(x – 9) – 3(x – 9) = 0 ⇒ (x – 3)(x – 9) = 0 ⇒ x = 3 और 9 ∴ समीकरण की दूसरी जड़ 9 है।

प्रश्न 4: यदि x⁶ + x⁵ + x⁴ + x³ + x² + x + 1 = 0, तो, x⁴² + x⁸⁴ का मान ज्ञात करें। (a) -1 (b) 1 (c) 2 (d) -2

उत्तर: (c) समाधान: दिए गए: x⁶ + x⁵ + x⁴ + x³ + x² + x + 1 = 0 ----(1) गणना: x से गुणा करते हैं, हमें मिलता है – ⇒ x⁷ + x⁶ + x⁵ + x⁴ + x³ + x² + x = 0 ----(2) समीकरण (2) – (1), हमें मिलता है – ⇒ x⁷ – 1 = 0 ⇒ x⁷ = 1। प्रश्न के अनुसार – x⁴² + x⁸⁴ का मान =

प्रश्न 5: वह द्विघात समीकरण खोजें जिसका एक मूल 5 = 2√5 है।

• (a) x² + 10x + 5 = 0
• (b) x² - 5x + 10 = 0
• (c) x² - 10x + 5 = 0
• (d) x² + 5x - 10 = 0

उत्तर: (c) हल: दिया गया: समीकरण का एक मूल 5 = 2√5 है। संकल्पना: यदि द्विघात समीकरण का एक मूल इस रूप में है (a√b), तो दूसरा मूल उसका संयुग्म (a - √b) होना चाहिए और इसके विपरीत।

द्विघात समीकरण: x² - (मूल का योग) (मूल का गुणनफल) = 0

गणना:

द्विघात समीकरण = x² - (α + β)x + αβ = 0

अब, द्विघात समीकरण = x² - 10x + 5 = 0

इसलिए, आवश्यक द्विघात समीकरण x² - 10x + 5 = 0 है।

प्रश्न 6: समीकरण ax² + bx = 0 के मूल समान हैं यदि:

• (a) b² = 4a
• (b) b² < />
• (c) b² > 4a
• (d) ab = 1/4

उत्तर: (d) हल: दिया गया: समीकरण ax² + bx = 0 है। उपयोग की गई संकल्पना: द्विघात समीकरण का सामान्य रूप ax² + bx + c = 0 है।

मूलों के लिए शर्तें:

• समान और वास्तविक मूल के लिए, b² – 4ac = 0
• असमान और वास्तविक मूल के लिए, b² – 4ac > 0
• कल्पनिक मूल के लिए, b² – 4ac < />

गणना: समान और वास्तविक मूल के लिए, b² – 4ac = 0 ⇒ b² = 4ac

द्विघात समीकरण के सामान्य रूप की तुलना करने पर हमें मिलेगा b = 1, a = a और c = b

तदनुसार, b² = 4ac ⇒ 1 = 4ab ⇒ ab = 1/4

इसलिए, सही संबंध ab = 1/4 है।

प्रश्न 7: समीकरण 5x² + 2x + Q = 2 का एक मूल दूसरे का व्युत्क्रम है। Q² का मान क्या है?

• (a) 25
• (b) 1
• (c) 49
• (d) 4

उत्तर: (c) हल: दिया गया: 5x² + 2x + Q = 2

दिया गया α = 1/β ⇒ α.β = 1 ----(i)

संकल्पना: मानक द्विघात समीकरण, ax² + bx + c = 0 को मानते हैं। α और β ऊपर दिए गए द्विघात समीकरण के दो मूल हैं।

मूलों का योग दिया गया है: α + β = -b/a = -(x के गुणांक/x² के गुणांक)

मूलों का गुणनफल दिया गया है: α × β = c/a = (स्थायी पद /x² के गुणांक)

गणना: मान लें कि 5x² + 2x + Q - 2 = 0 के मूल α और β हैं। प्रश्न के अनुसार, α = 1/β ⇒ α.β = 1

सामान्य समीकरण ax² + bx + c = 0 के साथ तुलना करें: a = 5, b = 2, c = Q - 2 ⇒ (Q – 2)/5 = 1 ⇒ Q - 2 = 5 ⇒ Q = 7

इसलिए, Q² = 7² = 49 है।

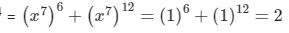
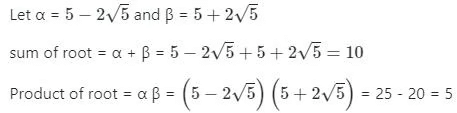
प्रश्न 8: यदि 3x² – ax – 6 = ax² + 2x + 2 का केवल एक (दोहराया हुआ) समाधान है, तो a का सकारात्मक पूर्णांक समाधान होगा: (क) 3 (ख) 2 (ग) 4 (घ) 5

उत्तर: (ख) समाधान: दिया गया: 3x² – ax – 6 = ax² + 2x + 2 ⇒ 3x² – ax² – ax – 6 – 2 = 0 ⇒ (3 – a)x² – (a + 2)x – 4 = 0 उपयोग किया गया सिद्धांत: यदि एक द्विघात समीकरण (ax² + bx + c = 0) के समान जड़ें हों, तो विवर्तनांक (discriminant) शून्य होना चाहिए अर्थात् b² – 4ac = 0 गणना: ⇒ D = B² – 4AC = 0 ⇒ (a + 2)² – 4(3 – a)(–4) = 0 ⇒ a² + 4a + 4 – 48 + 16a = 0 ⇒ a² + 20a – 44 = 0 ⇒ a² + 22a – 2a – 44 = 0 ⇒ a(a + 22) – 2(a + 22) = 0 ⇒ a = 2, -22 ∴ a का सकारात्मक पूर्णांक समाधान = 2

प्रश्न 9: 2 √5 और 2 − √5 के जड़ों के लिए द्विघात समीकरण है (क) x² - 4x - 1 = 0 (ख) x² + 4x - 1 = 0 (ग) x² - 4x + 1 = 0 (घ) x² + 4x + 1 = 0

उत्तर: (क) समाधान: दिया गया: दो जड़ें हैं 2 √5 और 2 - √5। उपयोग किया गया सिद्धांत: द्विघात समीकरण है: x² - (जड़ों का योग)x + (जड़ों का गुणनफल) = 0 गणना: मान लीजिए समीकरण की जड़ें A और B हैं। A = 2 √5 और B = 2 - √5 ⇒ A + B = 2 √5 + 2 - √5 = 4 ⇒ A × B = (2 √5)(2 - √5) = 4 - 5 = -1 तब समीकरण है ∴ x² - 4x - 1 = 0 गलती के बिंदु: एक द्विघात समीकरण के लिए, ax² + bx + c = 0, जड़ों का योग = (-b/a) = 4/1 और जड़ों का गुणनफल = c/a = -1/1 तब, b = -4 इसलिए, x का गुणांक नकारात्मक है।

प्रश्न 10: यदि α और β समीकरण x² – x – 1 = 0 के जड़ें हैं, तो समीकरण जिसकी जड़ें α/β और β/α हैं: (क) x² + 3x – 1 = 0 (ख) x² + x – 1 = 0 (ग) x² – x + 1 = 0 (घ) x² + 3x + 1 = 0

उत्तर: (घ) समाधान: दिया गया: x² – x – 1 = 0 उपयोग किया गया सूत्र: यदि दिया गया समीकरण ax² + bx + c = 0 है तो जड़ों का योग = -b/a और जड़ों का गुणनफल = c/a गणना: चूंकि α और β जड़ें हैं x² – x – 1 = 0, तब ⇒ α + β = -(-1) = 1 ⇒ αβ = -1 अब, यदि (α/β) और (β/α) जड़ें हैं, तब, ⇒ जड़ों का योग = (α/β) + (β/α) ⇒ जड़ों का योग = (α² + β²)/αβ ⇒ जड़ों का योग = [(α + β)² – 2αβ]/αβ ⇒ जड़ों का योग = (1)² – 2(-1)]/(-1) = -3 ⇒ जड़ों का गुणनफल = (α/β) × (β/α) = 1 अब, तब समीकरण है, ⇒ x² – (जड़ों का योग)x + (गुणनफल) = 0 ⇒ x² – (-3)x + (1) = 0 ⇒ x² + 3x + 1 = 0

प्रश्न 11: दिए गए प्रश्न में, दो समीकरण क्रमांक I और II दिए गए हैं। दोनों समीकरणों को हल करें और उपयुक्त उत्तर चुनें।

• I. x² – 2x – 80 = 0
• II. y² – 10y – 171 = 0

(a) x > y (b) x < y="" (c)="" x="" ≥="" y="" (d)="" x="y" या="" x="" और="" y="" के="" बीच="" संबंध="" स्थापित="" नहीं="" किया="" जा="" />

उत्तर: (d)

हल:

समीकरण I: x² – 2x – 80 = 0 ⇒ x² – 10x + 8x – 80 = 0 ⇒ x(x – 10) + 8(x – 10) = 0 ⇒ (x + 8)(x – 10) = 0 ⇒ x = -8, 10

समीकरण II: y² – 10y – 171 = 0 ⇒ y² – 19y + 9y – 171 = 0 ⇒ y(y – 19) + 9(y – 19) = 0 ⇒ (y – 19)(y + 9) = 0 ⇒ y = 19, -9

x और y के बीच तुलना (तालिका के माध्यम से):

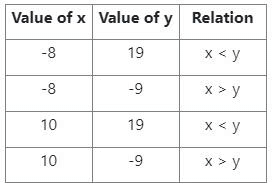
इसलिए x = y या संबंध स्थापित नहीं किया जा सकता।

प्रश्न 12: दिए गए प्रश्न में, दो समीकरण क्रमांक I और II दिए गए हैं। दोनों समीकरणों को हल करें और उपयुक्त उत्तर चुनें।

• I. x² + 8x – 48 = 0
• II. y² – 8y – 105 = 0

(a) x = y या x और y के बीच संबंध स्थापित नहीं किया जा सकता। (b) x > y (c) x < y="" (d)="" x="" ≤="" />

उत्तर: (a)

हल:

समीकरण I: x² + 8x – 48 = 0 ⇒ x² + 12x – 4x – 48 = 0 ⇒ x(x + 12) – 4(x + 12) = 0 ⇒ (x + 12) – 4(x + 12) = 0 ⇒ x = -12, 4

समीकरण II: y² – 8y – 105 = 0 ⇒ y² – 15y + 7y – 105 = 0 ⇒ y(y – 15) + 7(y – 15) = 0 ⇒ (y – 15)(y + 7) = 0 ⇒ y = 15, -7

x और y के बीच तुलना (तालिका के माध्यम से):

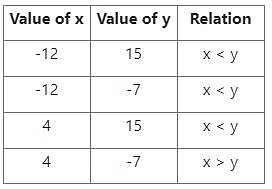
इसलिए x = y या x और y के बीच संबंध स्थापित नहीं किया जा सकता।

प्रश्न 13: दिए गए प्रश्न में, दो समीकरण क्रमांक I और II दिए गए हैं। दोनों समीकरणों को हल करें और उपयुक्त उत्तर चुनें।

• I. x² + x – 90 = 0
• II. y² + 4y – 96 = 0

(a) x < y="" (b)="" x="" ≤="" y="" (c)="" x="y" या="" x="" और="" y="" के="" बीच="" संबंध="" स्थापित="" नहीं="" किया="" जा="" सकता।="" (d)="" x="" ≥="" />

उत्तर: (c)

हल:

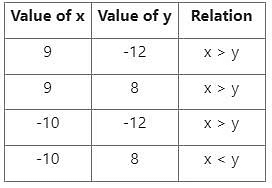
समीकरण I: x² + x – 90 = 0 ⇒ x² + 10x – 9x – 90 = 0 ⇒ x(x + 10) – 9(x + 10) = 0 ⇒ (x – 9)(x + 10) = 0 ⇒ x = 9, -10

समीकरण II: y² + 4y – 96 = 0 ⇒ y² + 12y – 8y – 96 = 0 ⇒ y(y + 12) – 8(y + 12) = 0 ⇒ (y + 12)(y – 8) = 0 ⇒ y = -12, 8

x और y के बीच तुलना (तालिका के माध्यम से):

तो x = y या x और y के बीच संबंध स्थापित नहीं किया जा सकता।

प्रश्न 14: यदि द्विघात समीकरण ax² + 2bx + c = 0 की जड़ें समान हैं, तो (a) a, b, c A.P में हैं (b) a, b, c G.P में हैं (c) a, b, c H.P में हैं (d) इनमें से कोई नहीं

उत्तर: (b) समाधान: अवधारणा: यदि ax² + bx + c = 0 की जड़ें समान हैं, तो D = b² - 4ac = 0

गणना: दिए गए द्विघात समीकरण ax² + 2bx + c = 0, जड़ें समान हैं यदि विभाजक (discriminant) शून्य है: (2b)² - 4ac = 0 ⇒ 4b² = 4ac ⇒ b² = ac ⇒ b = √ac

तो, सही उत्तर है (2) a, b, c ज्यामितीय प्रगति (Geometric Progression) में हैं।

प्रश्न 15: यदि x = -2/3, तो 9x² – 3x – 11 बराबर है (a) -13 (b) 13 (c) -5 (d) -17

उत्तर: (c) समाधान: दिए गए: x = -2/3

गणना: 9x² – 3x – 11 = ? ⇒ 9 × (-2/3)² – 3(-2/3) – 11 = ? ⇒ 9 × (4/9) – (-2) – 11 = ? ⇒ 4 + 2 – 11 = ? ⇒ 6 – 11 = ? ⇒ -5 = ?

∴ आवश्यक मान -5 है।