सारांश: औसत (Averages) | CSAT की तैयारी (हिंदी) - UPSC PDF Download

सीएसएटी में महत्व

यह अध्याय बेसिक न्‍यूमेरसी का सबसे महत्वपूर्ण अध्याय है जो सीएसएटी परीक्षाओं के लिए है। पिछले वर्षों के प्रश्नपत्रों के विश्लेषण से यह स्पष्ट है कि इस अध्याय से सीधे प्रश्न नहीं पूछे जाते, लेकिन इसके मूल सिद्धांत डेटा इंटरप्रिटेशन के लिए आवश्यक हैं। वर्ष 2024 में 2 प्रश्न पूछे गए थे और 2023 में 1 प्रश्न पूछे गए थे, जबकि वर्ष 2015-2022 के बीच लगभग 1-2 प्रश्न औसत के सीधे अनुप्रयोग पर पूछे गए थे।

औसत क्या है?

औसत को डेटा के एक सेट में केंद्रीय मान के रूप में परिभाषित किया जा सकता है।

• औसत को एक सेट में सभी मानों के योग को मानों की कुल संख्या से विभाजित करके सरलता से निकाला जा सकता है। दूसरे शब्दों में, एक औसत मान डेटा सेट का मध्य मान दर्शाता है। डेटा सेट किसी भी चीज़ का हो सकता है जैसे उम्र, पैसा, रन आदि।

उदाहरण: पहले पांच लगातार विषम संख्याओं का औसत क्या है?

समाधान:

पहली पांच लगातार विषम संख्याएं हैं: 1, 3, 5, 7, 9।

यहाँ, डेटा या अवलोकनों की संख्या 5 है और इन 5 संख्याओं का योग 25 है।

तो, औसत = 25 / 5 = 5।

औसत का अनुप्रयोग

प्रकार I: औसत उम्र

जब कोई व्यक्ति एक समूह को छोड़ता है और समूह में एक नया व्यक्ति उस स्थान पर शामिल होता है, तो:

(i) औसत उम्र में वृद्धि की स्थिति में,

नए व्यक्ति की उम्र = छोड़े गए व्यक्ति की उम्र (समूह में व्यक्तियों की संख्या × औसत उम्र में वृद्धि)

(ii) औसत उम्र में कमी होने पर,

नए व्यक्ति की उम्र = छोड़े गए व्यक्ति की उम्र - (समूह में व्यक्तियों की संख्या × औसत उम्र में कमी)

उदाहरण: 10 दोस्तों के एक समूह की औसत उम्र 10 वर्ष है। यदि इनमें से एक दोस्त समूह छोड़ देता है लेकिन उसकी जगह एक 22 वर्ष का दोस्त समूह में शामिल होता है, तो औसत उम्र 8 वर्ष हो जाती है। समूह से छोड़े गए दोस्त की उम्र ज्ञात करें।

• (a) 40 वर्ष
• (b) 42 वर्ष
• (c) 44 वर्ष
• (d) 46 वर्ष

हल: (b)

व्याख्या:

नए दोस्त की उम्र = छोड़े गए दोस्त की उम्र - [समूह में व्यक्तियों की संख्या × औसत उम्र में कमी]

⇒ 22 = छोड़े गए दोस्त की उम्र - (10 × (10 - 8))

∴ छोड़े गए दोस्त की उम्र = 22 + (10 × 2)

= 22 + 20

= 42 वर्ष

प्रकार II: संख्याओं का औसत

1. स्वाभाविक संख्याओं से संबंधित औसत

(i) n तक की लगातार स्वाभाविक संख्याओं का औसत

= (n + 1) / 2

(ii) n तक की लगातार स्वाभाविक संख्याओं के वर्गों का औसत

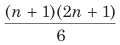
(iii) n तक की लगातार स्वाभाविक संख्याओं के घनों का औसत

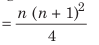
उदाहरण: पहले पांच स्वाभाविक संख्याओं के वर्गों का औसत ज्ञात करें।

• (a) 10
• (b) 11
• (c) 3
• (d) 5

हल: (b)

पहले पांच स्वाभाविक संख्याओं के वर्गों का औसत

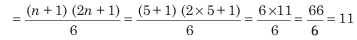
2. सम संख्याओं से संबंधित औसत

(i) n लगातार सम संख्याओं का औसत = (n + 1)

(ii) n लगातार सम संख्याओं के वर्गों का औसत =

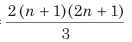
(iii) n तक के लगातार सम संख्याओं के वर्गों का औसत =

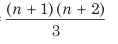
उदाहरण: 10 तक की लगातार सम संख्याओं के वर्गों का औसत ज्ञात करें।

समाधान: (b)

10 तक के लगातार सम संख्याओं का वर्ग का औसत

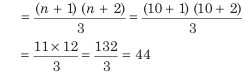
3. विषम संख्याओं से संबंधित औसत

(i) n लगातार विषम संख्याओं का औसत = n

(ii) n तक के लगातार विषम संख्याओं का औसत = (n + 1) / 2

उदाहरण: 9 तक के लगातार विषम संख्याओं का औसत निकालें।

(a) 4 (b) 5 (c) 7 (d) 9

समाधान: (b)

व्याख्या: 9 तक के लगातार विषम संख्याओं का औसत = (n + 1) / 2 = (9 + 1) / 2 = 10 / 2 = 5

प्रकार III औसत गति

1. यदि कोई निश्चित दूरी x km/h की गति से तय की जाती है और वही दूरी y km/h की गति से तय की जाती है, तो यात्रा के दौरान औसत गति है

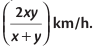
उदाहरण: यदि यात्रा का आधा भाग 15 km/h की गति से और अगला आधा भाग 12 km/h की गति से तय किया गया है, तो पूरे यात्रा के दौरान औसत गति निकालें।

समाधान:

औसत गति =

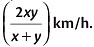
यहाँ, x = 15 और y = 12

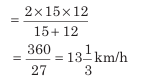
2. यदि कोई व्यक्ति या मोटर कार x km/h, y km/h, और z km/h की गति से तीन समान दूरी तय करता है, तो पूरे यात्रा के लिए औसत गति

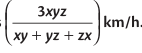
उदाहरण: एक ट्रेन पहले 160 किमी की यात्रा 120 km/h की गति से, अगला 160 किमी 140 km/h की गति से, और अंतिम 160 किमी 80 km/h की गति से तय करती है। पूरे यात्रा के लिए ट्रेन की औसत गति निकालें।

समाधान:

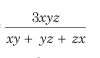
यहाँ, x = 120, y = 140 और z = 80

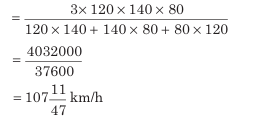
3. यदि कोई व्यक्ति A किमी की यात्रा x km/h की गति से, B किमी की यात्रा y km/h की गति से, और C किमी की यात्रा z km/h की गति से करता है, तो पूरे यात्रा के दौरान औसत गति

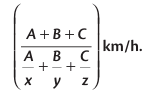
उदाहरण: एक व्यक्ति 3 km/h की गति से 9 किमी, 5 km/h की गति से 25 किमी, और 10 km/h की गति से 30 किमी की यात्रा करता है। पूरे यात्रा के लिए औसत गति निकालें।

समाधान:

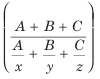
यहाँ, A= 9, B= 25, C=30, x= 3, y=5, z=10

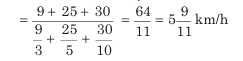
4. यदि कोई व्यक्ति दूरी के Aवें भाग को x किमी/घंटा की गति से, Bवें भाग को y किमी/घंटा की गति से, और शेष Cवें भाग को z किमी/घंटा की गति से कवर करता है, तो पूरे यात्रा के दौरान औसत गति है

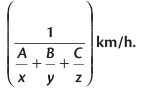
उदाहरण: एक ट्रेन 50% यात्रा को 30 किमी/घंटा की गति से, 25% यात्रा को 25 किमी/घंटा की गति से, और शेष को 20 किमी/घंटा की गति से कवर करती है। पूरे यात्रा के दौरान ट्रेन की औसत गति ज्ञात करें।

औसत गति=

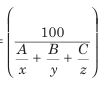
यहाँ, A=50, B=25, C=25, x=30, y=25 और z= 20

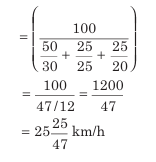
माध्यिका और मोड

• एक सीमित संख्या की सूची का माध्यिका सभी अवलोकनों को सबसे कम मान से सबसे अधिक मान तक व्यवस्थित करके और बीच का मान चुनकर ज्ञात की जा सकती है।
• मोड वह मान है जो सबसे अधिक बार आता है: मोड = 3*माध्यिका - 2*औसत

नोट:

प्रथम n क्रमिक प्राकृतिक संख्याओं का योग = [n(n + 1)]/2

प्रथम n क्रमिक प्राकृतिक संख्याओं का औसत = (n + 1)/2

शॉर्टकट तकनीकें
औसत पर आधारित प्रश्नों को आसानी से शॉर्टकट का उपयोग करके हल किया जा सकता है। शॉर्टकट का उपयोग करके, किसी भी प्रश्न को जल्दी और कुशलता से हल किया जा सकता है, जिससे समय की बचत होती है।

शॉर्टकट तकनीकें

औसत से संबंधित प्रश्नों को शॉर्टकट का उपयोग करके आसानी से हल किया जा सकता है। शॉर्टकट का उपयोग करके, किसी भी प्रश्न को तेजी से और प्रभावी ढंग से हल किया जा सकता है, जो बहुत सारा समय बचा सकता है।

1. औसत या औसत में परिवर्तन खोजने के लिए

उदाहरण 1:

किसी बल्लेबाज का औसत 16 पारियों में 36 है। अगली पारी में, वह 70 रन बनाता है। उसका नया औसत क्या होगा?

• a) 44
• b) 38
• c) 40
• d) 48

पारंपरिक तरीके से हल करना:

नया औसत = (पुराना योग + नया स्कोर)/(कुल पारियों की संख्या) = ((16 × 36) + 70)/((16 + 1)) = 38

शॉर्टकट तकनीक:

• चरण 1) नए स्कोर और पुराने औसत के बीच का अंतर लें = 70 – 36 = 34
• चरण 2) ये 34 अतिरिक्त रन हैं जो 17 पारियों में फैलते हैं। इसलिए, पारी का औसत 34/17 = 2 से बढ़ेगा।
• चरण 3) इसलिए, औसत बढ़ता है => 36 + 2 = 38।

यहां कुछ और औसत प्रश्न और उनके समाधान इसी तकनीक का उपयोग करके दिए गए हैं।

उदाहरण 2:

किसी विशेष विद्यालय में 19 बच्चों का औसत अंक 50 है। जब एक नए छात्र का अंक 75 आता है, तो कक्षा का नया औसत क्या होगा?

चरण 1) पुराने औसत और नए अंकों के बीच का अंतर लें = 75 - 50 = 25

चरण 2) यह 25 का स्कोर 20 छात्रों में वितरित होता है => 25/20 = 1.25

चरण 3) इसलिए, औसत 1.25 से बढ़ता है => 50 + 1.25 = 51.25।

2. एक और उदाहरण जहां औसत घटता है:

उदाहरण 3:

श्री मार्क के 3 बच्चों की औसत उम्र 8 वर्ष है। एक नया बच्चा पैदा होता है। सभी बच्चों की औसत उम्र ज्ञात कीजिए?

नई उम्र 0 वर्ष होगी। पुराने औसत और नई उम्र के बीच का अंतर = 0 - 8 = -8

यह 8 वर्ष की उम्र 4 बच्चों में फैली हुई है => (-8/4 = -2) इसलिए, औसत घटकर 8 - 2 = 6 वर्ष हो जाती है।

3. औसत दिया जाने पर नया मान खोजने के लिए:

29 छात्रों की औसत आयु 18 वर्ष है। यदि शिक्षक की आयु भी शामिल की जाए, तो कक्षा की औसत आयु 18.2 वर्ष हो जाती है। शिक्षक की आयु ज्ञात करें।

• a) 28
• b) 32
• c) 22
• d) 24

समाधान: पारंपरिक तरीके से हल करते हुए:

मान लेते हैं कि शिक्षक की औसत आयु = x (29 × 18 + x × 1) / 30

x के लिए हल करते हुए, हमें x = 24 मिलता है।

शॉर्टकट तकनीक:

शॉर्टकट का उपयोग करते हुए, पहले के समान विधि पर आधारित:

चरण 1: औसत में परिवर्तन की गणना करें = 18.2 – 18 = 0.2। यह परिवर्तन 30 के नमूने के आकार पर परिलक्षित होता है।

नया मान औसत से 30 × 0.2 = 6 वर्ष बढ़ जाता है, अर्थात् 18 + 6 = 24; जो कि शिक्षक की आयु है।

औसत ज्ञात करने के लिए विचलन की विधि

मानित औसत का सिद्धांत नया नहीं है। इसका उपयोग सांख्यिकी में औसत खोजने में गणना को कम करने के लिए किया जाता है, जहां डेटा बहुत बड़ा होता है।

यहाँ, हम कुछ औसत और भारित औसत पर आधारित क्षमता प्रश्नों को हल करने के लिए मानित औसत के अनुप्रयोग को प्रदर्शित करेंगे।

चलो समझने के लिए एक उदाहरण लेते हैं:

उदाहरण: 30 छात्रों की कक्षा में, औसत आयु 12 वर्ष है। यदि कक्षा के शिक्षक की आयु को शामिल किया जाए, तो कक्षा की नई औसत आयु 13 वर्ष हो जाती है। कक्षा शिक्षक की आयु ज्ञात करें।

मानक दृष्टिकोण

मानक दृष्टिकोण लागू करते हुए, 30 छात्रों की कुल आयु = 360 वर्ष। जब कक्षा शिक्षक को शामिल किया जाता है, तो कक्षा की नई कुल आयु = 403 वर्ष। ध्यान दें कि कुल आयु में वृद्धि केवल कक्षा शिक्षक के कारण है। इसलिए, कक्षा शिक्षक की आयु = 403 – 360 = 43 वर्ष है।

भिन्नता विधि

भिन्नता विधि को समझने के लिए, आइए हम समस्या का अनुकरण करें। औसत आयु के मामले में, मान लीजिए कि प्रत्येक छात्र के पास 12 चॉकलेट हैं।

• कक्षा के शिक्षक ने कुछ चॉकलेट लाने का निर्णय लिया और कक्षा में चॉकलेट का पुनर्वितरण इस प्रकार किया गया कि प्रत्येक व्यक्ति, जिसमें कक्षा के शिक्षक भी शामिल हैं, के पास समान संख्या में चॉकलेट हो; जिसका परिणाम हर व्यक्ति के लिए 13 चॉकलेट (नया औसत) है।
• अब, यह स्पष्ट है कि यदि कक्षा के शिक्षक केवल 12 चॉकलेट लाते हैं, तो औसत वही रहता है, अर्थात 12 ही (क्योंकि उनके पास चॉकलेट की संख्या समूह के औसत चॉकलेट की संख्या के बराबर है)।
• लेकिन यहाँ कक्षा के शिक्षकों के समावेश के साथ, औसत 1 से बढ़ जाता है। इसका मतलब है कि उन्होंने प्रत्येक छात्र को 1 चॉकलेट दी ताकि प्रत्येक 30 छात्रों के पास अब 13 चॉकलेट हों।

इसलिए, उन्होंने 30 × 13 = 390 चॉकलेट लाए। या कक्षा के शिक्षक की आयु 43 वर्ष है।

औसत के बारे में महत्वपूर्ण तथ्य

• यदि प्रत्येक संख्या में एक निश्चित मात्रा n बढ़ाई/घटाई जाती है, तो औसत भी उसी मात्रा से बढ़ता या घटता है।
• यदि प्रत्येक संख्या को एक निश्चित मात्रा n से गुणा/भाग किया जाता है, तो औसत भी उसी मात्रा से गुणा या भाग होता है।
• यदि आधी संख्याओं में एक ही मान जोड़ा जाता है और दूसरी आधी संख्याओं से वही मान घटाया जाता है, तो औसत के अंतिम मान में कोई परिवर्तन नहीं होगा।

वजनी औसत

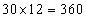
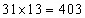
भारित अंकगणितीय औसत, जिसे सामान्यतः दर्शाया जाता है

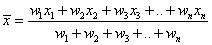
जहाँ x1, x2, x3, …, xn औसत हैं और w1, w2, w3, .., wn उनके संबंधित वजन हैं।

उदाहरण: 25 लड़कों और 15 लड़कियों की एक कक्षा में, लड़कों और लड़कियों के औसत ऊँचाई क्रमशः 150 सेंटीमीटर और 140 सेंटीमीटर है। कक्षा की औसत ऊँचाई ज्ञात करें।

मानक विधि:

लड़कों के समूह का कुल वजन = और लड़कियों के समूह का कुल वजन = इसलिए, कक्षा की औसत ऊँचाई =

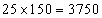
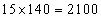
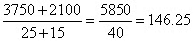
विचलन विधि:

मान लें कि प्रत्येक लड़का और प्रत्येक लड़की क्रमशः 150 और 140 चॉकलेट ले जा रहे हैं।

• हमें कुल चॉकलेट वितरित करनी है ताकि प्रत्येक लड़का और लड़की समान संख्या में चॉकलेट ले जाए। चूंकि प्रत्येक लड़का प्रत्येक लड़की से 10 चॉकलेट अधिक ले जा रहा है, इसलिए हम प्रत्येक लड़के से 10 चॉकलेट ले लेते हैं ताकि अब प्रत्येक लड़का और लड़की 140 चॉकलेट ले जाए। हमारे पास अतिरिक्त चॉकलेट की मात्रा समान है।

• ये अतिरिक्त चॉकलेट लड़कों और लड़कियों के बीच समान रूप से वितरित की जानी हैं। इसलिए, प्रत्येक को =6.25 और चॉकलेट मिलेगी। इसलिए कक्षा की औसत = 140 + 6.25 = 146.25 सेंटीमीटर।

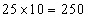
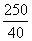
हल किए गए उदाहरण

प्रश्न 1: EPL में चयनित 15 खिलाड़ियों द्वारा औसतन 16 गोल किए गए हैं। एक खिलाड़ी द्वारा किए गए अधिकतम गोल 20 हैं और न्यूनतम 12 हैं। खिलाड़ियों द्वारा किए गए गोल 12 से 20 के बीच हैं। अधिकतम कितने खिलाड़ी ऐसे हो सकते हैं जिन्होंने कम से कम 18 गोल किए हैं?

• c) 9
• d) 6
• e) इनमें से कोई नहीं

समाधान: विकल्प (c)

18 या उससे अधिक गोल करने वाले खिलाड़ियों की संख्या को अधिकतम करने के लिए, यह मान लेना चाहिए कि केवल एक व्यक्ति ने 20 गोल किए हैं। इसके विपरीत, एक व्यक्ति 12 गोल करेगा।

यानी, 15 - 2 = 13 खिलाड़ी बचे हैं।

अब, हर दो खिलाड़ियों के लिए जो 18 गोल कर रहे हैं, एक खिलाड़ी 12 गोल करेगा। यह औसत 16 तक पहुँचने के लिए किया जाता है। हमारे पास 8 खिलाड़ी होंगे जिनका स्कोर 18 है और 4 खिलाड़ी होंगे जिनका स्कोर 12 है। अंतिम खिलाड़ी का स्कोर 16 होगा। इस प्रकार, 18 और उससे अधिक गोल करने वालों की अधिकतम संख्या = 9।

प्रश्न 2: 8 लड़कियों के समूह का औसत वजन 50 किलोग्राम है। यदि 2 लड़कियाँ R और S, P और Q की जगह लेती हैं, तो नया औसत वजन 48 किलोग्राम हो जाता है। P का वजन = Q का वजन और R का वजन = एक और लड़की T का वजन जो समूह में शामिल है और नए औसत वजन से 48 किलोग्राम हो जाता है। T का वजन = R का वजन। P का वजन ज्ञात करें?

• a) 48 किलोग्राम
• b) 52 किलोग्राम
• c) 46 किलोग्राम
• d) 56 किलोग्राम

समाधान: विकल्प (d)

8 x 50 - R - S - P - Q = 48 × 8

R - S - P - Q = -16

P - Q - R - S = 16

R = S और P = Q

P - R = 8

एक और व्यक्ति शामिल किया जाता है और वजन = 48 किलोग्राम

मान लीजिए कि वजन a है = (48 × 8 - a) / 9 = 48

A = 48 किलोग्राम = R का वजन

=> P का वजन = 48 + 8 = 56 किलोग्राम।

प्रश्न 3: EPL में 15 चयनित खिलाड़ियों द्वारा किए गए लक्ष्यों की औसत संख्या 16 है। एक खिलाड़ी द्वारा बनाए गए लक्ष्यों की अधिकतम संख्या 20 है और न्यूनतम 12 है। खिलाड़ियों द्वारा बनाए गए लक्ष्य 12 और 20 के बीच हैं। कम से कम 18 गोल करने वाले खिलाड़ियों की अधिकतम संख्या क्या हो सकती है? क) 10 ख) 5 ग) 9 घ) 6

हल: विकल्प (ग) 18 गोल या उससे अधिक करने वाले खिलाड़ियों की संख्या को अधिकतम करने के लिए, यह मान लेना चाहिए कि केवल एक व्यक्ति ने 20 गोल किए हैं। इसके विपरीत, एक व्यक्ति 12 गोल करेगा। अर्थात्, 15 - 2 = 13 खिलाड़ी शेष हैं।