Practice Questions: Ratio & Proportion | General Test Preparation for CUET UG - CUET Commerce PDF Download
| Table of contents |

|
| Introduction |

|
| Easy Level |

|
| Medium Level |

|
| Hard Level |

|
Introduction
This practice document is designed to help you prepare for the CUET UG exam by strengthening your concepts across varying levels of difficulty—Easy, Medium, and Hard. It focuses on foundational understanding with basic concepts, followed by more challenging problems to improve your problem-solving speed and accuracy. The main idea of this document is to practice the questions before you go and attempt your nationwide tests @EduRev so that you will be more relating to questions asked in that exam & be more confident about your answers.
All The Best!
Easy Level
At this level, questions are targeted to improve your knowledge of basic concepts. These are extremely important for conceptual understanding at the foundation level.
Let's start with the practice questions
Example 1: If three numbers are in the ratio of 1 : 3 : 5 and half the sum is 9, then the ratio of cubes of the numbers is:
(a) 6 : 12 : 13
(b) 1 : 3 : 25
(c) 1 : 27 : 125
(d) 3 : 5 : 7
Ans. (c)
Solution: 1 : 3 : 5So x, 3x and 5x add up to 18.
So the numbers are 2, 6 and 10.
Ratio of cubes = 8 : 216 : 1000 = 1: 27: 125.
Example 2: Three quantities A, B, C are such that AB = KC, where k is a constant. When A is kept constant, B varies directly as C; when B is kept constant, A varies directly C and when C is kept constant, A varies inversely as B. Initially, A was at 5 and A : B : C was 1 : 3 : 5. Find the value of A when B equals 9 at constant C.
(a) 8
(b) 8.33
(c) 9
(d) 9.5
Ans. (b)
Solution:
Initial values are 5, 15 and 25.Thus we have 5 * 15 = K * 25.
Hence, K = 3.
Thus, the equation is AB = 3C.
For the problem, keep C constant at 25.
Then, A * 9 = 3 * 25. i.e., A = 75/9 = 8.33
Example 3: A began a business with Rs. 4,500 and was joined afterwards by B with Rs. 5,400. If the profits at the end of the year were divided in the ratio 2 : 1, then B joined the business after:
(a) 5 months
(b) 4 months
(c) 6 months
(d) 7 months
Ans. (d)
Solution:The ratio of profit-sharing = 4500 × 12: 5400 × n where n is the period for which B invested.
Ratio = 4500 × 12 : 5400 × n = 10 : n
Now, this ratio is equal to 2 : 1
∴ 10 : n = 2 : 1 ⇒ n = 5 monthsThus, B joined A after 12 – 5 = 7 months
 |
Practice Test: Ratio & Proportion- 2
|
Start Test |
Medium Level
Almost 70% of questions in exams are of Medium difficulty level. Though the conceptually they seem easier, the trick is to solve the calculations faster & we curated problems for you to help you do problems easier.
Example 1: Monthly incomes of X and Y are in the ratio 1 : 3 and their expenses are in the ratio 19 : 40. X saves Rs. 18,860 less than that Y and in total they save Rs. 36,020. The income of X and Y respectively are:
(a) Rs. 10,480 and Rs. 31440
(b) Rs. 9,000 and Rs. 27,000
(c) Rs. 14,200 and Rs. 42,600
(d) Rs. 18,000 and Rs. 31,440
Ans. (a)
Solution: Let the income of X be Rs. p and income of Y be Rs. 3p
Let expenses of X be Rs. 19q and expenses of Y be Rs. 40q
Hence, savings of X = Rs. (p – 19q) and savings of Y = Rs. (3p – 40q)Total savings = (4p – 59q) = 36020
Difference of savings = (2p – 21q) = 18860
Solving the above equations, we get p = 10480
Thus, the income of X and Y is Rs. 10,480 and Rs. 31, 440, respectively.
Example 2: A student scored marks in the ratio 5 : 4 : 6 : 8 : 7 in five subjects having equal maximum marks. In all, he scored 50% of the maximum marks in all the five subjects taken together. In how many subjects did he score more than 55% of the maximum marks?
(a) 1
(b) 2
(c) 3
(d) 4
Ans. (b)
Solution: Let his marks be 5x, 4x, 6x, 8x, and 7x respectively.
Aggregate marks obtained = 30x = 50% of aggregate maximum marks.
Thus, aggregate maximum marks = 60x
Maximum marks per subject = 12 x 55% of maximum marks per subject = 6.6x
Hence in two subjects, marks are more than 6.6x.
Example 3: A person buys some apples and mangoes from the market. The cost price of a mango is twice that of an apple and the selling price of a mango is thrice that of an apple. By selling an apple at twice its cost price, he makes 150% profit on the whole. Find the ratio of the number of mangoes to that of apples that he bought from the market.
(a) 3 : 5
(b) 3 : 4
(c) 1 : 2
(d) 2 : 3
Ans. (c)
Solution: Suppose the person buys apples and M mangoes and the cost price of an apple is Rs. x.
Therefore, the cost price of the mango will be 2x.
Total cost price = Ax + 2Mx.
Now the selling price of an apple is 2x.
∴ SP of a mango will be 6x.
Total SP = 2Ax + 6Mx.
Now we have 2Ax + 6Mx = 5 2 (Ax + 2Mx) or M/A=½.
Hard Level
Many questions of such difficulty comes into CUET UG exam. These will help you to develop the deep conceptual understanding. Lets start with examples.
Example 1: From a full barrel containing 729 litres of honey, we pour off ‘a’ litre and add water to fill up the barrel. After stirring the solution thoroughly, we pour off ‘a’ litre of the solution and again add water to fill up the barrel. After the procedure is repeated 6 times, the solution in the barrel contains 64 litres of honey. Find a.
(a) 243 litres
(b) 81 litres
(c) 2.7 litres
(d) 3 litres
Ans. (a)
Solution:
Check each of the options as follows: Suppose you are checking option b which gives the value of as 81 litres. Then, it is clear that when you are pouring out 81 litres, you are leaving 8/9 of the honey in the barrel.
Thus, the amount of honey contained after 6 such operations will be given by
= 729 X (8/9)6. If this answer has to be correct, this value must be equal to 64 (which it clearly is not since the value will be in the form of a fraction.)Hence, this is not the correct option. You can similarly rule out the other options.
Example 2: There are two alloys of gold, silver and platinum. The first alloy is known to contain 40 per cent of platinum and the second alloy 26 per cent of silver. The percentage of gold is the same in both alloys. Having alloyed 150 kg of the first alloy and 250 kg of the second, we get a new alloy that contains 30 per cent of gold. How many kilograms of platinum is there in the new alloy?
(a) 170 kg
(b) 175 kg
(c) 160 kg
(d) 165 kg
Ans. (a)
Solution: Since the percentage of gold in both alloys is the same, any mixture of the two will contain the same percentage concentration of gold.
Hence, we get
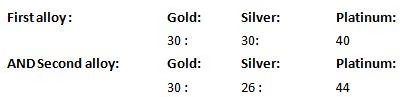
This brings you to the end of the practice document. EduRev wishes you the best for your online practice tests on our platform.
|
164 videos|606 docs|954 tests
|
FAQs on Practice Questions: Ratio & Proportion - General Test Preparation for CUET UG - CUET Commerce
| 1. What are the basic concepts of ratio and proportion? |  |
| 2. How do you solve problems involving ratios? |  |
| 3. Can you give an example of a practical application of ratios and proportions? |  |
| 4. What are some common mistakes to avoid when working with ratios and proportions? |  |
| 5. How can I practice ratio and proportion problems effectively? |  |
















