गणितीय क्रियाएँ | CSAT की तैयारी (हिंदी) - UPSC PDF Download
परिचय
इस प्रकार की समस्याओं के लिए मूल दृष्टिकोण कोडिंग और डिकोडिंग के समान है। इसमें प्रतीकों या ज्यामितीय आकृतियों और उनके अर्थों का ध्यानपूर्वक अध्ययन करना होता है। फिर, प्रश्नों का उत्तर देने के लिए उन प्रतीकों के स्थान पर अर्थों का उपयोग किया जाना चाहिए।
संकेत और संकेतन
इन प्रकार के प्रश्नों के लिए प्रतीक गणितीय ऑपरेशनों जैसे +, –, ×, ÷, >, <, ³,="" £,="और" #="" का="" प्रतिनिधित्व="" करते="" हैं।="" इसलिए,="" छात्रों="" को="" प्रतीकों="" को="" गणितीय="" ऑपरेशनों="" से="" बदलना="" चाहिए="" और="" दिए="" गए="" अभिव्यक्ति="" का="" मूल्य="" निकालने="" के="" लिए="" bodmas="" नियम="" का="" पालन="" करना="" चाहिए।="" अन्य="" प्रतीक="" जैसे="" dñ,="" *,="" @,="" $,="" आदि="" का="" उपयोग="" उचित="" परिभाषाओं="" के="" साथ="" किया="" जा="" सकता="">
उदाहरण 1: यदि ' ' का अर्थ '–' है, '–' का अर्थ '×' है, '×' का अर्थ ' ' है और '÷' का अर्थ ' ' है, तो 15 × 3 ÷ 15 5 – 2 = ? (क) 0 (ख) 10 (ग) 20 (घ) 6
सही उत्तर विकल्प (ख) है। चिह्न बदलने के बाद = 15 = 3 15 – 5 × 2 = 5 15 – 10 = 10।
उदाहरण 2: यदि 2 * 3 = 12, 3 * 4 = 20 और 4 * 5 = 30, तो 2 * 6 है (क) 18 (ख) 12 (ग) 21 (घ) इनमें से कोई नहीं।
सही उत्तर विकल्प (ग) है।
दोनों पक्षों के संख्याएँ * के साथ एक बढ़ाई जाती हैं और फिर उत्तर प्राप्त करने के लिए गुणा किया जाता है। 2*6 = 3 × 7 = 21।
उदाहरण 3: यदि x $ y = (x y xy –1) (x y xy 1), तो (4 $ 10) का मान है। (क) 2915 (ख) 2195 (ग) 2951 (घ) 2955

सही उत्तर विकल्प (a) है। $ के परिभाषा के अनुसार, (4$10) होगा (4 10 4 × 10 - 1) (4 10 4 × 10 1) = 2915। इसलिए, उत्तर (a) है।
उदाहरण 4: यदि * का अर्थ है "से बड़ा है", @ का अर्थ है "से छोटा है"; और $ का अर्थ है "बराबर है" और यदि a $ b और b @ c, तो (a) c * b (b) b * c (c) c * a (d) (a) और (c) दोनों।
सही उत्तर विकल्प (d) है। प्रतीकों को उनके दिए गए अर्थ के साथ बदलें। यदि a $ b और b @ c का अर्थ होगा a = b और b < c,="" तो="" c="" /> b या c > a यानी, c * b, c * a दिए गए विकल्पों से सही हैं।
ज्यामितीय आकृतियाँ
ये आकृतियाँ कई हिस्सों में विभाजित की जाएँगी, जिनमें से प्रत्येक भाग में एक संख्या या एक अक्षर भरा जाएगा, सिवाय एक भाग के। आकृतियों में संख्याएँ या अक्षर एक विशेष पैटर्न का पालन करते हैं। उद्देश्य इस पैटर्न की पहचान करना और गायब संख्या या अक्षर को खोजना है। ज्यामितीय आकृतियों पर आधारित समस्याएँ विभिन्न प्रकार की होती हैं।
प्रकार 1: वृत्तों पर आधारित
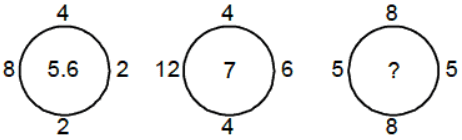
इस प्रकार में, तीन वृत्त दिए जाएंगे जिनके बाहर संख्याएँ होंगी। पहले दो वृत्तों में, वृत्त के अंदर की संख्या एक विशेष पैटर्न के अनुसार लिखी गई है। छात्र का उद्देश्य तीसरे वृत्त की गायब संख्या को खोजना है।
- उदाहरण 5: (a) 7.16 (b) 9.25 (c) 6.23 (d) 8.33
सही उत्तर विकल्प (a) है।
वृत्त के अंदर की संख्या = √16 + √10 = 4 + 3.16 = 7.16
उदाहरण 6: (a) 14 (b) 10 (c) 6 (d) 4
सही उत्तर विकल्प (d) है। वृत्त के बाहर की संख्याओं का घनमूल वृत्त के अंदर की संख्या देता है।
प्रकार 2: भागों में विभाजित वृत्त
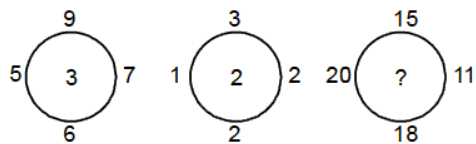
ऐसे प्रश्नों में, वृत्त को तीन भागों में विभाजित किया जाता है। संख्याओं पर एक अंकगणितीय क्रिया करने से गायब संख्या मिलती है।
- उदाहरण 7: (a) 2 (b) 11 (c) 33 (d) 44
सही उत्तर विकल्प (b) है। 60 - 40 = 10, 20 - 29 = 7, गायब संख्या 55 - 66 = 11 है।
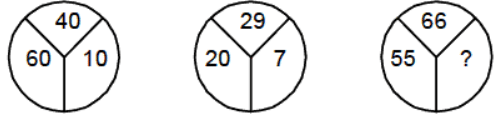
उदाहरण 8: (a) 9 (b) 6 (c) 8 (d) 4
सही उत्तर विकल्प (d) है। (11 – 4)2 = 49, (3 – 2)2 = 1, गायब संख्या (20 – 18)2 = 4 है।
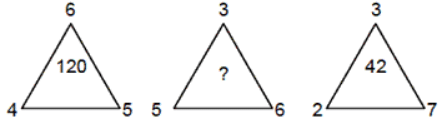
प्रकार 3: त्रिकोणों पर आधारित समस्याएँ
ऐसे प्रश्नों में, तीन त्रिकोण दिए जाते हैं जिनमें अंदर और बाहर संख्याएँ होती हैं। त्रिकोण के अंदर की संख्या बाहर की संख्याओं पर कुछ अंकगणितीय ऑपरेटरों का उपयोग करके प्राप्त की जाती है।
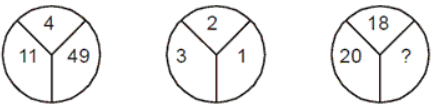
- उदाहरण 9: (a) 2 (b) 1 (c) 0 (d) इनमें से कोई नहीं
सही उत्तर विकल्प (d) है। (5 + 7 + 4) ÷ 4 = 4, गायब संख्या (1 + 2 + 1) ÷ 4 = 1 है।
उदाहरण 10: (a) 70 (b) 80 (c) 90 (d) 1
सही उत्तर विकल्प (c) है। (4 × 5 × 6) = 120, गायब संख्या (5 × 6 × 3) = 90 है।
प्रकार 4: वर्गों पर आधारित समस्याएँ
ऐसे प्रश्नों में तीन वर्ग होते हैं जिनमें पाँच संख्याएँ होती हैं, इनमें से 4 संख्याएँ वर्ग के चार कोनों पर होती हैं और एक मध्य संख्या कुछ अंकगणितीय क्रिया का पालन करती है।
- उदाहरण 11: (a) 4 (b) 6 (c) 5 (d) 7
सही उत्तर विकल्प (c) है। गायब संख्या = ...
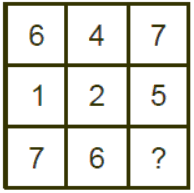
प्रकार 5: मैट्रिक्स पर आधारित समस्याएँ
ऐसे प्रश्नों में, एक वर्ग को नौ भागों में विभाजित किया गया है, तीन पंक्तियाँ और तीन कॉलम हैं, जिनमें से नौ भागों में से आठ भाग भरे होते हैं और एक भाग खाली रहता है। छात्रों को गायब संख्या खोजने के लिए कुछ अंकगणितीय क्रिया का उपयोग करना पड़ता है।
- उदाहरण 12: (a) 8 (b) 9 (c) 13 (d) 12
सही उत्तर विकल्प (d) है। (6 + 1) = 7, (4 + 2) = 6, कॉलम के अनुसार -4। गायब संख्या = 7 - 5 = 12 है।
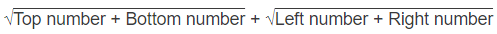
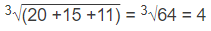

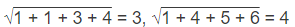
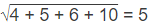
|
67 videos|98 docs|119 tests
|




















