उदाहरण (हल के साथ): पाई चार्ट | CSAT की तैयारी (हिंदी) - UPSC PDF Download
प्रश्न 1: यदि एनआरआई द्वारा निवेश 4000 करोड़ रुपये है, तो कॉरपोरेट हाउस और एफआईआई द्वारा मिलकर किया गया निवेश कितना है:
- a.) 24000 करोड़
- b.) 24363 करोड़
- c.) 25423.4 करोड़
- d.) 25643.3 करोड़
उत्तर: यदि एनआरआई द्वारा किया गया निवेश 4000 करोड़ रुपये है, जो कुल मूल्य का 11% है।
फिर, कुल मूल्य होगा = 4000 * 100/11
= 36363.63
अब, कॉरपोरेट हाउस और एफआईआई द्वारा मिलकर किया गया निवेश 36363.63 का 67% होगा, अर्थात् 24,363.63 करोड़।
प्रश्न 2: कुल निवेश का कितना प्रतिशत एफआईआई या एनआरआई से आ रहा है?
- a.) 33%
- b.) 44%
- c.) 11%
- d.) 22%
उत्तर 2: यह एक बहुत सीधा प्रश्न है और उत्तर 44% है।
प्रश्न 3: यदि एफआईआई और कॉरपोरेट हाउस के अलावा कुल निवेश 335,000 करोड़ रुपये है, तो एनआरआई और ऑफशोर फंड का निवेश (लगभग) कितना होगा:
- a.) 274,100
- b.) 285,600
- c.) 293,000
- d.) निर्धारित नहीं किया जा सकता
उत्तर 3: यह प्रश्न पहले प्रश्न की तरह हल किया जाएगा। एफआईआई और कॉरपोरेट हाउस के अलावा कुल निवेश 33% है, जो 335,000 करोड़ रुपये है।
फिर सभी का कुल निवेश होगा 335,000 * 100/33
= 1015151.5151
और एनआरआई और ऑफशोर फंड कुल निवेश का 27% बनाते हैं। इसलिए, 0.27 * 1015151.5151, अर्थात् 274,090.90।
प्रश्न 4: एनआरआई से कॉरपोरेट हाउस में भारत बांड में निवेश प्रवाह का अनुमानित अनुपात क्या है?

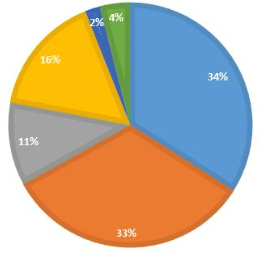
a.) 1:4
b.) 1:3
c.) 3:1
उत्तर 4: यह एक सरल प्रश्न है। NRI द्वारा निवेश 11% है और कॉर्पोरेट हाउस का निवेश 34% है। इसलिए, अनुपात 11:34 होगा, अर्थात् लगभग 1:3।
प्रश्न 5: कॉर्पोरेट क्षेत्र में, केंद्रीय कोण में लगभग कितनी डिग्री होनी चाहिए?
a.) 120
b.) 121
c.) 122
d.) 123
उत्तर 5: प्रश्न को हल करने के लिए आपको प्रतिशत को डिग्री में बदलना सीखना होगा और यह काफी सरल है। आपको बस प्रतिशत को 360° से गुणा करना है, अर्थात् 11/100 * 360° = 39.6°।
अब इस प्रश्न में, हमें कॉर्पोरेट हाउस का केंद्रीय कोण निकालना है, अर्थात् 0.34 का 360° का गुणा, अर्थात् 122.4°।
प्रश्न 6: यदि अगले वर्ष FII से कुल निवेश प्रवाह को दोगुना किया जाए और सभी अन्य स्रोतों से निवेश प्रवाह इस वर्ष अपने मौजूदा स्तर पर स्थिर रहें, तो अगले वर्ष (लगभग) भारतीय बांड में FII निवेश का अनुपात क्या होगा?
a.) 40%
b.) 50%
c.) 60%
d.) 70%
उत्तर 6: वर्तमान में FII का हिस्सा 100 में से 33 है।
यदि इनका मूल्य दोगुना किया जाता है और सभी अन्य निवेश स्थिर रखे जाते हैं, तो उनका नया मूल्य 66 होगा, जो 133 में से होगा = लगभग 50%।
प्रश्न 7: यदि दोगुना होने के बाद (पिछले प्रश्न में) FII का प्रवाह US$ 500 मिलियन के बराबर है, तो भारतीय बांड में कुल निवेश US$ में क्या होगा?
a.) 1000
b.) 1500
c.) 800
उत्तर 7: 500 मिलियन कुल निवेश का 50% है, जैसा कि हमने पिछले प्रश्न में पाया। इसलिए, कुल निवेश होगा 500 * 100/50 अर्थात् 1000 मिलियन डॉलर।
उदाहरण 2: निम्नलिखित चित्र का ध्यान से अध्ययन करें और प्रश्नों के उत्तर दें:
मानव शरीर का प्रतिशत संगठन
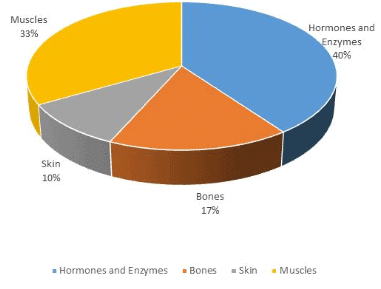
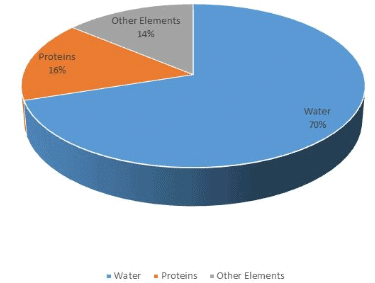
प्रश्न 1: मानव शरीर के कुल वजन का कितना प्रतिशत मानव शरीर की त्वचा में प्रोटीन के वजन के बराबर है?
- a.) 0.016
- b.) 1.6
- c.) 0.16
- d.) निर्धारित नहीं किया जा सकता
उत्तर 1: इस प्रश्न का समाधान करने के लिए आपको दोनों पाई चार्ट का उपयोग करना होगा। चूंकि शरीर में प्रोटीन का कुल प्रतिशत 16% है। और, मानव शरीर में त्वचा का कुल प्रतिशत 10% है। इसलिए, त्वचा में प्रोटीन का प्रतिशत 10% का 16 है, अर्थात् 1.6।
प्रश्न 2: 50 किलोग्राम वजन वाले व्यक्ति के शरीर में पानी की मात्रा क्या होगी?
- a.) 20 किलोग्राम
- b.) 35 किलोग्राम
- c.) 41 किलोग्राम
- d.) 5 किलोग्राम
उत्तर 2: पानी शरीर का 70% बनाता है। इसलिए, यदि व्यक्ति का वजन 50 किलोग्राम है, तो इसका 70% पानी होगा। पानी का वजन 35 किलोग्राम होगा।
प्रश्न 3: मांसपेशियों में प्रोटीन के वितरण के अनुपात और हड्डियों में प्रोटीन के वितरण के अनुपात का क्या है?
- a.) 1:18
- b.) 1:2
- c.) 2:1
- d.) 18:1
उत्तर 3: फिर से, दोनों पाई चार्ट का उपयोग करते हुए, हम जानते हैं कि शरीर के वजन का 33% मांसपेशियों में है जबकि 17% हड्डियों में है और इसका 16% प्रोटीन होगा।
इसलिए, 0.16*33: 0.16*17, जो लगभग 2:1 के बराबर है।
प्रश्न 4: मानव शरीर में प्रोटीन और अन्य सूखे तत्वों के वितरण को दिखाने के लिए, वृत्त का आर्क केंद्र पर कोण बनाना चाहिए;
- a.) 54o
- b.) 126o
- c.) 108o
- d.) 252o
उत्तर 4: उदाहरण 1 में दिए गए सूत्र का उपयोग करते हुए, उत्तर 5 हमें मिलता है,
[(16% + 14%)/100] * 360o = 108o.
प्रश्न 5: मानव शरीर का ऐसा कौन सा भाग है जो न तो हड्डियों से बना है और न ही त्वचा से?
- a.) 1/40
- b.) 3/80
- c.) 2/5
- d.) इनमें से कोई नहीं
उत्तर 5: अब हम मान लेते हैं कि शरीर को - संख्या के रूप में 1 और 17/100 तथा 10/100 हड्डियों और त्वचा के रूप में माना जाता है, अर्थात् 1/6 और 1/10
इसलिए, आवश्यक उत्तर है 1 – (1/6 + 1/10) = 11/15.
XAT 2012: निम्नलिखित पाई चार्ट एक बल्लेबाज द्वारा टेस्ट पारी में बनाए गए रन के प्रतिशत वितरण को दर्शाता है।
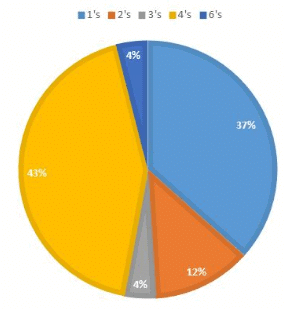
प्रश्न 1: यदि बल्लेबाज ने कुल 306 रन बनाए हैं, तो उसने कितने 4 और 6 मारे?
- a.) 31 और 3 क्रमशः
- b.) 32 और 2 क्रमशः
- c.) 32 और 3 क्रमशः
- d.) 33 और 1 क्रमशः
- e.) 33 और 2 क्रमशः
उत्तर 1: एक बल्लेबाज द्वारा बनाए गए कुल रन 306 हैं। 4 और 6 के द्वारा मारे गए % क्रमशः 43 और 4 हैं।
इस प्रकार, 4 के लिए 0.43 * 306/4 और 6 के लिए 0.04 * 306/6 क्रमशः 4 और 6 थे।
अर्थात, 33 और 2.
प्रश्न 2: यदि 5 डॉट बॉल 4 के लिए मारी गई हैं, और यदि बल्लेबाज द्वारा किए गए दो शॉट्स जिनसे उसने प्रत्येक में 3 रन बनाए थे, यदि एक रन की जगह एक रन ही मिलता, तो 4 के लिए बनाए गए रन के प्रतिशत के लिए क्षेत्र का केंद्रीय कोण क्या होगा?
- a.) 160
b.) 163
c.) 165
d.) 167
e.) 170
उत्तर 2: चूंकि एक बल्लेबाज द्वारा बनाए गए कुल रन 306 हैं, इसलिए 4 के माध्यम से प्राप्त कुल रन 306 का 0.43 हैं, अर्थात् 132। अब अगर इसमें 5 और चौके जोड़े जाते हैं, तो कुल 152 हो जाता है।
अब 5 चौके जोड़ने और 2 तीनों को घटाने और साथ ही 2 एकों को जोड़ने के बाद बल्लेबाज द्वारा प्राप्त कुल रन 306 + 16 = 322 है।
4 के लिए केंद्रीय कोण होगा 152/322 * 360 = 170°।
SNAP 2005: वित्तीय वर्ष 2004-05 के लिए एक समूह की कंपनियों की क्षेत्रवार बिक्री का अध्ययन करें और निम्नलिखित प्रश्न का उत्तर दें:
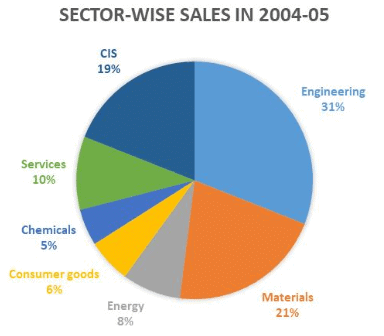
प्रश्न 1: इस समूह की कंपनियाँ कई क्षेत्रों में काम करती हैं। होल्डिंग कंपनी ने समूह की बिक्री का एक बड़ा हिस्सा (कम से कम 80%) एक साथ योगदान देने वाले क्षेत्रों की न्यूनतम संख्या (5 से अधिक नहीं) की निगरानी करने का निर्णय लिया है। सही क्षेत्रों का सेट पहचानें।
- a.) इंजीनियरिंग, सेवाएँ, CIS और उपभोक्ता सामान
- b.) इंजीनियरिंग, सेवाएँ, CIS, ऊर्जा और उपभोक्ता सामान
- c.) इंजीनियरिंग, सामग्री, सेवाएँ और CIS
d.) इंजीनियरिंग, सामग्री, CIS और ऊर्जा
उत्तर 1: इस प्रश्न का समाधान बहुत आसान है। बस पाई चार्ट का उपयोग करें और चार सबसे अधिक योगदान देने वाले क्षेत्रों को जोड़ें, यानी इंजीनियरिंग, सामग्री, CIS, सेवाएँ। उनका कुल योग
(33 21 19 10) 91% है यानी 80% से अधिक।
प्रश्न 2: क्षेत्रों के बीच बिक्री के मुकाबले औसत लाभ 10% है जबकि इंजीनियरिंग का लाभ मार्जिन 12% और CIS का 20% है। शेष क्षेत्रों में औसत लाभ क्या है?
- a.) 5.87%
- b.) 6.12%
- c.) 4.94%
- d.) 4%
उत्तर 2: कुल बिक्री = 782,750।
औसत लाभ = 10% यानी 78,275
इंजीनियरिंग और CIS का लाभ क्रमशः 244,830 का 12% और 148,160 का 20% है, यानी 29,379.6 और 29,632।
इसलिए, शेष क्षेत्रों का लाभ 78,275 – 59,011.6 = 19,263.4 है।
इस प्रकार, शेष क्षेत्रों के लिए औसत लाभ का % (19,263.4/ 78,275) * 100/5 = 4.94% है।
CAT 2018: नीचे दिया गया बहु-स्तरीय पाई-चार्ट 2016 और 2017 के दौरान एक बड़े रिटेल इलेक्ट्रॉनिक्स आउटलेट के लिए LED टेलीविज़न सेट की बिक्री को दर्शाता है। बाहरी परत इस अवधि के दौरान मासिक बिक्री को दर्शाती है, जिसमें प्रत्येक लेबल उस महीने के बाद उस महीने की बिक्री संख्या दर्शाता है। कुछ महीनों के लिए, चार्ट में बिक्री की संख्या नहीं दी गई है। मध्य परत तिमाही के अनुसार कुल बिक्री की संख्या दिखाती है (कुछ मामलों में, तिमाही के बगल में कुल तिमाही बिक्री संख्या नहीं दी गई है)। सबसे अंदरूनी परत वार्षिक बिक्री को दर्शाती है। यह ज्ञात है कि 2016 की दूसरी तिमाही (अप्रैल, मई, जून) के तीन महीनों के दौरान बिक्री की संख्या एक अंकगणित प्रगति बनाती है, जैसे कि उस वर्ष की चौथी तिमाही (अक्टूबर, नवंबर, दिसंबर) में तीन-मासिक बिक्री की संख्या।
प्रश्न 1: दिसंबर 2017 में बिक्री में प्रतिशत वृद्धि क्या है, दिसंबर 2016 की बिक्री की तुलना में?
- a.) 38.46
- b.) 22.22
- c.) 50.00
- d.) 28.57
प्रश्न 2: 2017 के किस तिमाही में 2016 की समान तिमाही की तुलना में बिक्री में प्रतिशत वृद्धि सबसे अधिक थी?
- a.) Q4
- b.) Q1
- c.) Q2
- d.) Q3
प्रश्न 3: पिछले तिमाही की बिक्री की तुलना में बिक्री में प्रतिशत कमी किस तिमाही में सबसे अधिक थी?
- a.) 2016 का Q2
- b.) 2017 का Q2
- c.) 2017 का Q4
- d.) 2017 का Q1
प्रश्न 4: पिछले महीने की बिक्री की तुलना में बिक्री में प्रतिशत वृद्धि किस महीने में सबसे अधिक थी?
- a.) अक्टूबर 2017
- b.) अक्टूबर 2016
- c.) मार्च 2016
- d.) मार्च 2017
उत्तर: प्रश्नों को आसानी से हल करने के लिए, हम पहले दिए गए जानकारी को एक संकुचित तालिका में प्रस्तुत कर सकते हैं ताकि इसे पढ़ना और समझना आसान हो सके।
| महीना/ बिक्री आंकड़ा | 2016 | 2017 |
|---|---|---|
| Q1 जनवरी | 80 | 120 |
| फरवरी | 60 | 100 |
| मार्च | 100 | 160 |
| Q2 अप्रैल | 40 | 60 |
| मई | 75 | |
| जून | 65 | |
| Q3 जुलाई | 75 | 60 |
| अगस्त | 120 | |
| सितंबर | 55 | 70 |
| Q4 अक्टूबर | 100 | 150 |
| नवंबर | 170 | |
| दिसंबर |
जैसा कि आप ऊपर की तालिका में देख सकते हैं, कुछ महीनों की बिक्री गायब है और हमें सबसे पहले दिए गए जानकारी से उनका मूल्यांकन करना होगा और फिर ऊपर दिए गए प्रश्नों के उत्तर खोजने होंगे।
अब, प्रश्न में यह दिया गया है कि 2016 में अप्रैल, मई और जून के महीने एक A.P. (Arithmetic Progression) का निर्माण करते हैं, और इसी तरह 2016 की चौथी तिमाही के महीने, अर्थात् अक्टूबर, नवंबर, दिसंबर भी।
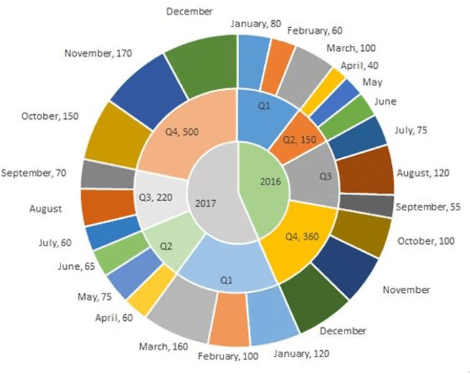
क्वार्टर 2 में कुल बिक्री = 150
मान लें कि a-d, a, a+d ए.पी. (Arithmetic Progression) के तीन पद हैं।
इसलिए, a-d, a, a+d = 150
- 3a = 150
- a = 50
चूंकि, अप्रैल की बिक्री 40 है, अर्थात् a-d = 40
- d = 10
इसका उपयोग करके, हम आसानी से बाकी महीनों की बिक्री के मान निकाल सकते हैं, अर्थात् 50 और 60 क्रमशः।
इसी तरह, उपरोक्त विधि का उपयोग करके, हम नवंबर'16 और दिसंबर'16 के लिए मान निकाल सकते हैं। इस मामले में, a होगा 120 और d = 20।
इस प्रकार, इन महीनों की बिक्री क्रमशः 120 और 140 है।
अब जैसा कि आप तालिका में देख सकते हैं, हमने दिसंबर'17 और अगस्त'17 को छोड़कर सभी गायब मासिक बिक्री के आंकड़े निकाल लिए हैं, जिन्हें आसानी से ज्ञात किया जा सकता है।
क्वार्टर 4 में कुल बिक्री 2017 = 500
और अक्टूबर'17 और नवंबर'17 में बिक्री क्रमशः 150 और 170 है।
इसलिए, दिसंबर की बिक्री = 500 - 150 - 170 = 180 और इसी प्रकार, अगस्त'17 की बिक्री = 220 - 60 - 70 = 90
इसलिए, हमारी तालिका निम्नलिखित बनती है,
| महीना/बिक्री आंकड़ा | 2016 | 2017 | |||
|---|---|---|---|---|---|
| क्वार्टर 1 | जनवरी | 80 | 240 | 120 | 380 |
| क्वार्टर 2 | अप्रैल | 40 | 150 | 60 | 200 |
| मई | 50 | 75 | |||
| जून | 60 | 65 | |||
| क्वार्टर 3 | जुलाई | 75 | 250 | 60 | 220 |
| अगस्त | 120 | 90 | |||
| क्वार्टर 4 | अक्टूबर | 100 | 300 | 150 | 500 |
| नवंबर | 120 | 170 | |||
| दिसंबर | 140 | 180 |
अब हम ऊपर दी गई तालिका का उपयोग करके सभी प्रश्नों का उत्तर देने के लिए तैयार हैं।
उत्तर 1: दिसंबर'17 की बिक्री में दिसंबर'16 की तुलना में प्रतिशत वृद्धि = (180 - 140)/140 × 100 = 40/140 × 100 = 28.57%
उत्तर 2: हमें प्रतिशत के संदर्भ में बिक्री में सबसे उच्च वृद्धि वाले क्वार्टर का मूल्यांकन करने की आवश्यकता है।
| क्वार्टर | बिक्री में वृद्धि | प्रतिशत के संदर्भ में |
|---|---|---|
| क्वार्टर 1 | 40 | 58.33% |
| क्वार्टर 2 | 50 | 33.33% |
| क्वार्टर 3 | (30) | (12%) |
| क्वार्टर 4 | 0 | 66.67% |
इस प्रकार, उपरोक्त तालिका का उपयोग करते हुए, हमें उत्तर मिलता है कि क्वार्टर 4 है।
उत्तर 3: जैसा कि हम तालिका से स्पष्ट रूप से देख सकते हैं, बिक्री में गिरावट केवल 2016 और 2017 के दोनों वर्षों के क्वार्टर 2 में है।
Q2-2016 में गिरावट = (240 - 150)/240 × 100 = 37.5%
Q2-2017 में गिरावट = (380 - 200)/380 × 100 = 47.37%
इस प्रकार, उत्तर है तिमाही 2’2017
उत्तर 4: दिए गए विकल्प केवल मई और अक्टूबर के लिए हैं और हम देख सकते हैं कि अक्टूबर 2017 में बिक्री नवंबर में 70 से बढ़कर 150 हो गई है, इसलिए यह अन्य दिए गए महीनों की तुलना में सबसे अधिक है। सही विकल्प a) अक्टूबर 2017
|
67 videos|98 docs|119 tests
|















