डेटा केसलेट्स: परिचय और समाधान किए गए उदाहरण | CSAT की तैयारी (हिंदी) - UPSC PDF Download

केसलेट क्या हैं?

• एक केसलेट एक छोटे केस अध्ययन की तरह है जो एक व्यापार समस्या या स्थिति का वर्णन करता है, जिसे अक्सर डेटा द्वारा समर्थन प्राप्त होता है।
• केसलेट डेटा व्याख्या प्रश्न वे प्रश्न हैं जो यह परीक्षण करते हैं कि कोई व्यक्ति दी गई डेटा को एक छोटे, कहानी जैसे परिदृश्य में कितनी अच्छी तरह समझता और विश्लेषण करता है।
• ये प्रश्न यह देखने के लिए डिज़ाइन किए गए हैं कि क्या कोई व्यक्ति दिए गए डेटा को पढ़ सकता है और उसकी व्याख्या कर सकता है, उसे समझ सकता है, और अपनी समझ के आधार पर प्रश्नों का उत्तर दे सकता है।
• इसके लिए, उन्हें विशिष्ट जानकारी खींचनी पड़ सकती है, पैटर्न या प्रवृत्तियों को पहचानना पड़ सकता है, और अपने निष्कर्षों के आधार पर सुझाव भी देने पड़ सकते हैं।

केसलेट पढ़ते समय, हमेशा महत्वपूर्ण तथ्यों और आकड़ों को रेखांकित करना उचित है, और यदि आवश्यक हो, तो प्रश्नों को हल करने के लिए अपनी तालिका/चार्ट/ग्राफ बनाना चाहिए।

केसलेट दो रूपों में हो सकते हैं:

अब डेटा को समझने के लिए हम उदाहरणों का उपयोग करेंगे और चरण-दर-चरण समाधान खोजने की कोशिश करेंगे जो परीक्षा में केसलेट प्रश्नों को हल करने में मदद कर सके। उदाहरणों पर जाने से पहले, निम्नलिखित बिंदुओं को ध्यान में रखें जो आपको केसलेट की समस्या का समाधान निकालने में सहायता करेंगे।

• पैराग्राफ को ध्यान से पढ़ें और उन चर को पहचानें जिनके चारों ओर पूरा पैराग्राफ घूमता है और जिन पर प्रश्न पूछे जाते हैं। सभी महत्वपूर्ण बिंदुओं को नोट करें।
• चारों के बीच संबंधों को चित्रात्मक रूप से तालिकाओं, प्रतीकों या वैन आरेखों का उपयोग करके बनाने की कोशिश करें। तालिकाएँ बहुविध संबंधों को स्पष्ट रूप से परिभाषित करने में मदद करती हैं, इसलिए उन्हें अधिक बार उपयोग करने का प्रयास करें।
• डेटा व्याख्या आमतौर पर संख्यात्मक और अंकगणितीय गणनाओं की आवश्यकता होती है जैसे कि औसत, अनुपात, प्रतिशत आदि। इनके अवधारणाओं में पूर्णता रखें और तेज़ गणनाओं के लिए शॉर्टकट और तरकीबों का उपयोग करें, यह आपको बहुत समय बचाएगा।
• जो जानकारी दी नहीं गई है, उसे न मानें और पैराग्राफ में दी गई छिपी हुई जानकारी को खोजने के लिए तर्क और तर्कशक्ति का उपयोग करें।
• जब अनुमान या सापेक्ष मान पूछे जाते हैं, तो लंबी गणनाओं में न फंसें। केवल वही गणना करें जो पूछी गई है।

1. तर्क पर आधारित पैराग्राफ

अब हम तर्क आधारित एक उदाहरण पर चलते हैं। नीचे दिए गए प्रश्न पर विचार करें।

एक खेल प्रतियोगिता में, छह टीमें (A, B, C, D, E और F) एक दूसरे के खिलाफ प्रतिस्पर्धा कर रही हैं। मैच दो चरणों में निर्धारित हैं। प्रत्येक टीम चरण - I में तीन मैच खेलती है और चरण - II में दो मैच। कोई भी टीम किसी अन्य टीम के खिलाफ एक से अधिक बार नहीं खेलती है। किसी भी मैच में टाई की अनुमति नहीं है। चरण - I और चरण - II के पूर्ण होने के बाद की टिप्पणियाँ निम्नलिखित हैं।

चरण-I: एक टीम ने सभी तीन मैच जीते।

• दो टीमों ने सभी मैच हार दिए। D ने A के खिलाफ हार मान ली लेकिन C और F के खिलाफ जीत हासिल की।
• E ने B के खिलाफ हार मान ली लेकिन C और F के खिलाफ जीत हासिल की।
• B ने कम से कम एक मैच हार दिया।
• F ने चरण-I की शीर्ष टीम के खिलाफ नहीं खेला।

चरण-II: चरण-I के नेता ने अगले दो मैच हार दिए।

• चरण-l के बाद नीचे की दो टीमों में से एक टीम ने दोनों मैच जीतें, जबकि दूसरी टीम ने दोनों मैच हारें।
• एक और टीम ने चरण-II में दोनों मैच हारें।

प्रश्न 1: वे दो टीमें जो चरण-I के नेता को हराने में सफल रहीं, वे हैं:

(1) F & D (2) E & F (3) B & D (4) E & D (5) F & D

प्रश्न 2: एकमात्र टीम(टीमें) जो चरण-II में दोनों मैच जीती है(हैं) वह(वे) है(हैं) :

(1) B (2) E & F (3) A, E & F (4) B, E & F (5) B & F

प्रश्न 3: वे टीमें जो प्रतियोगिता में ठीक दो मैच जीतने में सफल रहीं, वे हैं:

(1) A, D & F (2) D & E (3) E & F (4) D, E & F (5) D & F

प्रश्न 4: प्रतियोगिता में सबसे अधिक जीतने वाली टीम(टीमें) हैं:

(1) A (2) A & C (3) F (4) E (5) B & E

चरण-दर-चरण समाधान

चरण-दर-चरण समाधान

अब हम ऊपर दिए गए प्रश्न के लिए एक क्रमबद्ध समाधान तैयार करेंगे। सबसे पहले, हम प्रश्न में दिए गए सभी महत्वपूर्ण बिंदुओं को नोट करेंगे।

6 टीमें हैं: A, B, C, D, E, और F। चरण 1 में 3 मैच और चरण 2 में 2 मैच हैं। प्रत्येक टीम एक बार केवल दूसरी टीम के खिलाफ खेलती है। खेल में कोई टाई नहीं होती।

इन बिंदुओं को ध्यान में रखते हुए और चरण 1 के बारे में दिए गए जानकारी का उपयोग करते हुए, हम इसके लिए एक तालिका बनाएंगे।

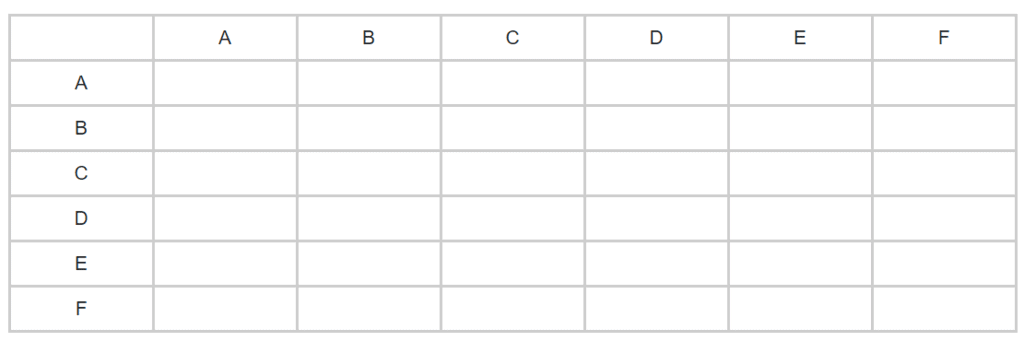
हम एक-एक करके चरण 1 में दिए गए सभी बिंदुओं की व्याख्या करेंगे और दो टीमों के बीच कोई मैच नहीं होने के लिए x का उपयोग करेंगे और जीतने और हारने वाली टीमों के लिए won और loss का उपयोग करेंगे। पहला बयान है:

• एक टीम ने सभी 3 मैच जीते। लेकिन इस समय हमारे पास यह जानने की कोई अन्य जानकारी नहीं है कि कौन सी टीम हारी या जीती, इसलिए हम बाद में इस बिंदु पर वापस आएंगे।
• दो टीमों ने सभी मैच हारे। हालांकि, यह एक उपयोगी जानकारी है क्योंकि 6 टीमों में से 2 ने सभी मैच हारे, लेकिन हमारे पास यह जानने के लिए कोई और जानकारी नहीं है कि कौन सी टीम है, इसलिए हम आगे बढ़ेंगे।
• हमें दिया गया है कि D ने A के खिलाफ हार मानी। इसलिए, हम पंक्ति 5 और कॉलम 1 में हार को लिखेंगे। इसके अलावा, हम D को उन टीमों में से हटा देंगे जिन्होंने सभी मैच जीते। इसके बाद, D ने C और F के खिलाफ भी जीत हासिल की।

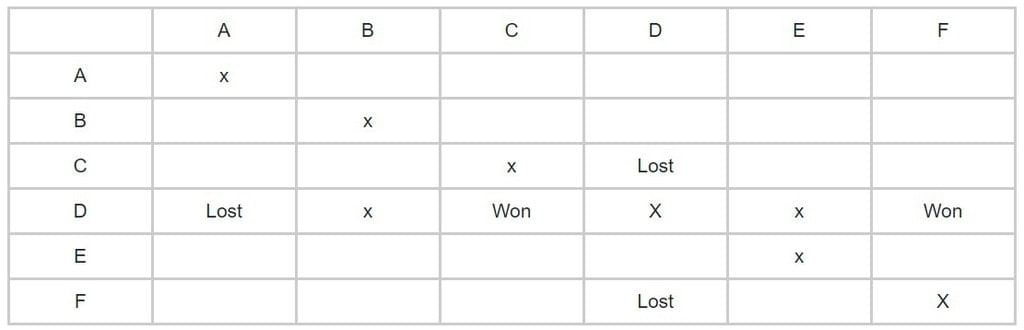
• चूंकि कोई टीम एक-दूसरे के खिलाफ नहीं खेल सकती। इसलिए, हमने वहां x रखा है। इसके अलावा, सभी टीमें केवल 3 मैच खेलती हैं। D और B तथा D और E के बीच कोई मैच नहीं होगा।
• एक बार फिर, जैसा कि दिया गया है कि E ने B के खिलाफ हार मानी लेकिन C और F के खिलाफ जीत हासिल की। इसलिए, E को भी उन टीमों से हटा दिया गया है जिन्होंने सभी मैच जीते या सभी मैच हारे। इस प्रकार, E और A तथा E और D के बीच कोई मैच नहीं होगा।

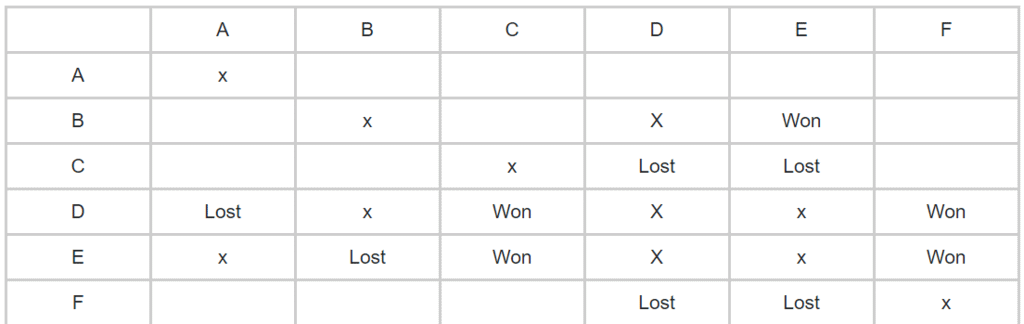
• क्योंकि B ने कम से कम एक मैच हारा है। इसलिए, B सभी जीतने वाली टीम नहीं है। और B हारने वाली टीम भी नहीं होगी। चूंकि, सभी B, C, D, E, और F ने कम से कम एक मैच हारा है, इसलिए A ही एकमात्र टीम रह गई है और इस प्रकार वह सभी जीतने वाली टीम बन गई।
• F जीतने वाली टीम यानी A के खिलाफ नहीं खेलता। इस प्रकार, C और F सभी हारने वाली टीमें बन जाती हैं। और यही तालिका बनेगी।

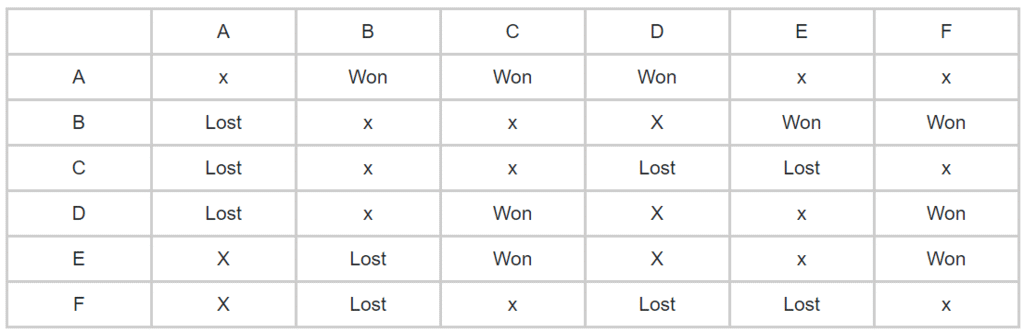
अब हम चरण 2 की ओर बढ़ेंगे और एक तालिका बनाने के लिए आगे बढ़ेंगे।

• हमें दिया गया है कि कोई भी टीम एक ही टीम के खिलाफ इवेंट में एक बार से अधिक नहीं खेलती। इसलिए, हमने स्टेज 1 में एक-दूसरे के खिलाफ खेली गई सभी टीमों के नीचे एक x रखा।
• स्टेज 1 में नेता ने 2 मैच हारे। चूंकि A नेता है, इसलिए A अगले चरण में सभी मैच हारने वाला होगा। इसके अलावा, हर टीम का एक ही मैच अन्य टीमों के खिलाफ होता है, इसलिए A E और F के खिलाफ हार जाएगा।
• अब, दो हारने वाली टीमों में से एक ने अगले दो मैच जीते और एक ने सभी हारे। चूंकि F ने A के खिलाफ जीत हासिल की, इसलिए F जीती हुई टीम होगी और C हारने वाली टीम होगी।

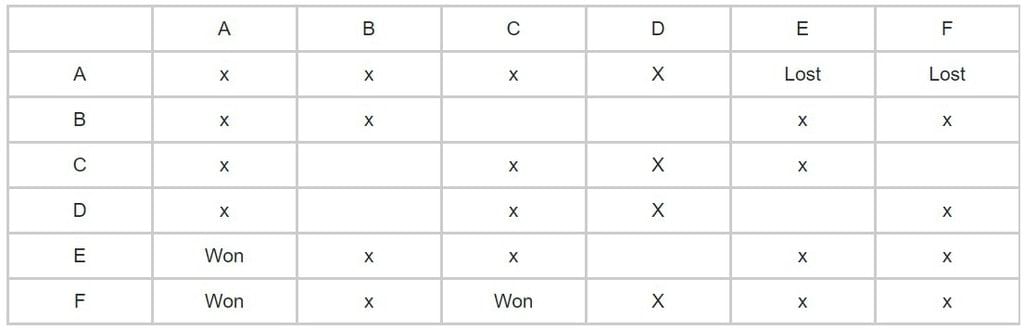
• इसके अलावा, एक और टीम है जिसने दोनों मैच हारे और यह E नहीं हो सकती क्योंकि यह A के खिलाफ जीती है और B भी नहीं हो सकती क्योंकि C को दोनों मैच हारने के लिए B का जीतना अनिवार्य है। इसलिए, D ने भी दोनों मैच हारे।

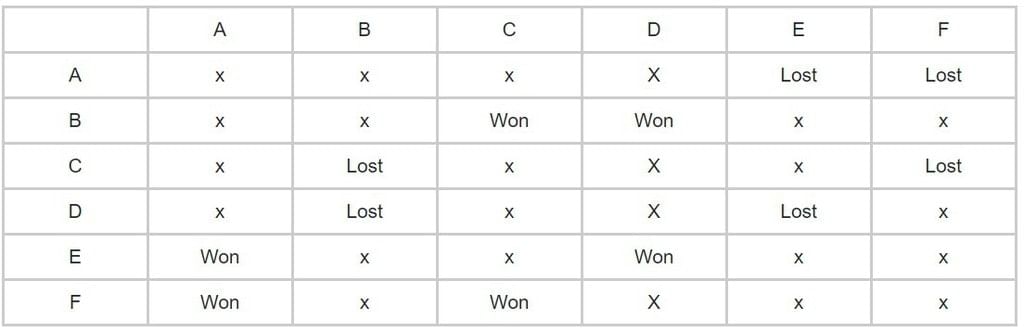
अब हम इस समस्या से संबंधित किसी भी प्रश्न का उत्तर देने की स्थिति में हैं। इसलिए, हम इन तालिकाओं पर आसानी से देख सकते हैं और ऊपर दिए गए प्रश्न का उत्तर दे सकते हैं। इसी तरह के दृष्टिकोण का उपयोग करते हुए, हम कई ऐसे Caselet reasoning प्रश्नों को हल कर सकते हैं।

2. संख्यात्मक डेटा पर आधारित पैराग्राफ

अब चलिए संख्यात्मक डेटा पर आधारित पैराग्राफ के एक उदाहरण की ओर बढ़ते हैं। नीचे दिए गए प्रश्न पर विचार करें।

दो व्यापारी, चेतन और माइकल, पांच व्यापारिक दिनों में MCS शेयरों की खरीद और बिक्री में शामिल थे। पहले दिन की शुरुआत में, MCS शेयर की कीमत ₹100 थी, जबकि पांचवे दिन के अंत में यह ₹110 थी। प्रत्येक दिन के अंत में, MCS शेयर की कीमत या तो ₹10 बढ़ी, या फिर ₹10 कम हुई। चेतन और माइकल ने प्रत्येक व्यापारिक दिन के अंत में खरीद और बिक्री के निर्णय लिए। किसी दिए गए दिन पर MCS शेयर की प्रारंभिक कीमत पिछली दिन की समाप्ति मूल्य के समान थी। चेतन और माइकल ने एक समान संख्या में शेयर और नकद के साथ शुरुआत की और दोनों के पास पर्याप्त मात्रा में थे। यहां कुछ अतिरिक्त जानकारी दी गई है कि चेतन और माइकल ने पांच व्यापारिक दिनों में कैसे व्यापार किया।

• प्रत्येक दिन यदि कीमत बढ़ती है, तो चेतन अंतिम कीमत पर 10 शेयर MCS के बेचता है। दूसरी ओर, यदि कीमत घटती है, तो वह अंतिम कीमत पर 10 शेयर खरीदता है।
• यदि किसी दिन की अंतिम कीमत ₹110 से ऊपर थी, तो माइकल 10 शेयर MCS के बेचता था, जबकि यदि यह ₹90 से नीचे थी, तो वह 10 शेयर खरीदता था, सभी अंतिम कीमत पर।

प्रश्न 1: यदि चेतन ने तीन लगातार दिनों में MCS के 10 शेयर बेचे, जबकि माइकल ने पांच दिनों में केवल एक बार 10 शेयर बेचे, तो दिन 3 के अंत में MCS की कीमत क्या थी? (1) ₹90 (2) ₹100 (3) ₹110 (4) ₹120 (5) ₹130

प्रश्न 2: यदि चेतन के पास दिन 5 के अंत में माइकल की तुलना में ₹1300 अधिक नकद था, तो दिन 4 के अंत में MCS शेयर की कीमत क्या थी? (1) ₹90 (2) ₹100 (3) ₹110 (4) ₹120 (5) अद्वितीय निर्धारण योग्य नहीं

प्रश्न 3: यदि माइकल के पास दिन 5 के अंत में चेतन की तुलना में 20 अधिक शेयर थे, तो दिन 3 के अंत में शेयर की कीमत क्या थी? (1) ₹90 (2) ₹100 (3) ₹110 (4) ₹120 (5) ₹130

प्रश्न 4: यदि माइकल के पास दिन 5 के अंत में चेतन की तुलना में ₹100 कम नकद था, तो दिन 5 के अंत में माइकल और चेतन के पास कितने शेयरों का अंतर था? (1) माइकल के पास चेतन से 10 कम शेयर थे। (2) माइकल के पास चेतन से 10 अधिक शेयर थे। (3) चेतन के पास माइकल से 10 अधिक शेयर थे। (4) चेतन के पास माइकल से 20 अधिक शेयर थे। (5) दोनों के पास समान संख्या में शेयर थे।

उपरोक्त केसलेट और उनसे जुड़े प्रश्नों को हल करने के लिए, हम सभी उपर्युक्त बिंदुओं को ध्यान में रखते हुए इसी तरह से आगे बढ़ेंगे। इस बार हम महत्वपूर्ण बिंदुओं का उपयोग करके एक तालिका बनाएंगे।

• इस मामले में, दो लोग हैं - माइकल और चेतन। पहले दिन की शुरुआत में कीमत Rs.100 है और पांचवे दिन के अंत में कीमत Rs.110 है।
• हर दिन की कीमत में उतार-चढ़ाव होता है, या तो Rs.10 बढ़ती है या Rs.10 घटती है। और उस दिन की समाप्ति मूल्य अगले दिन का प्रारंभिक मूल्य बन जाता है।
• उपरोक्त बिंदुओं का उपयोग करते हुए, 10 विभिन्न मामलों को बनाया जा सकता है और एक तालिका इस प्रकार बनाई जा सकती है:

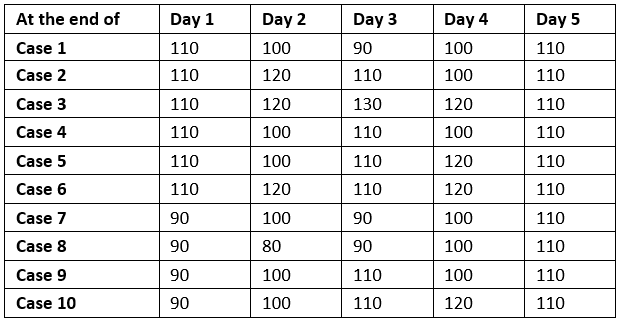
अब, माइकल और चेतन के बारे में दिए गए दो बिंदुओं की मदद से और कीमतों में वृद्धि और कमी के प्रति उनकी प्रतिक्रिया के आधार पर, हम सीधे समस्या के सभी निम्नलिखित प्रश्नों को हल करेंगे।

प्रश्न 1: बताया गया है कि चेतन ने लगातार 3 दिनों में 10 शेयर बेचे और चेतन केवल तब शेयर बेचता है जब कीमतें बढ़ती हैं। इस प्रकार, चेतन के संबंध में सहसंबंधित मामले हैं - केस 3, केस 8, केस 10। इसके अलावा, माइकल ने सभी 5 दिनों में केवल एक बार 10 शेयर बेचे, जबकि चेतन ने तीन बार बेचे। और माइकल केवल तभी बेचता है जब समापन मूल्य 110 से ऊपर हो। अब, तीनों मामलों की तुलना करके और माइकल के कारक को जोड़कर, हम आसानी से एकमात्र केस 10 पर पहुँच सकते हैं। इसलिए, हमारे समाधान का केस केस 10 है। अतः प्रश्न का उत्तर 110 है।

प्रश्न 2: यदि पांचवे दिन के अंत में चेतन के पास माइकल से 1300 अधिक नकद है। इस स्थिति के घटित होने की संभावना हो सकती है:

अब इन सभी मामलों में, चौथे दिन के अंत में शेयर की कीमत ₹100 है।

प्रश्न 3 मान लेते हैं कि चैतन और माइकल दोनों ने x संख्या में शेयरों से शुरुआत की। अब पांचवें दिन के अंत में, माइकल के पास चैतन की तुलना में 20 अधिक शेयर हैं। हम पिछले प्रश्नों के समान तर्क करेंगे, लेकिन अब अर्जित राशि के बजाय, हम शेयरों की संख्या की गणना करेंगे।

माइकल के पास चैतन की तुलना में 20 अधिक शेयर होने की केवल एक ही संभावना है। इसलिए, तीसरे दिन के अंत में कीमत ₹90 है।

प्रश्न 4 हमें यह पता करना है कि माइकल के पास चैतन की तुलना में ₹100 कम हैं। हम उपरोक्त तरीके से आगे बढ़ेंगे।

अब जैसा कि हम देख सकते हैं, दोनों मामलों में, माइकल और चैतन के पास समान संख्या में शेयर हैं। इसलिए, विकल्प (5) सही है।

डेटा केसलेट प्रश्नों को हल करने के लिए सुझाव

• एक तालिका बनाएं: डेटा को प्रभावी ढंग से व्यवस्थित करने के लिए एक तालिका बनाएं। केसलेट पढ़ते समय नोटेशन का उपयोग करें ताकि तालिका को भर सकें।
• ध्यान से पढ़ें: त्रुटियों से बचने के लिए केसलेट के विवरण पर ध्यान दें। सुनिश्चित करें कि सभी डेटा की इकाइयाँ मेल खाती हैं और जो मेल नहीं खाती उन्हें परिवर्तित करें।
• बुनियादी बातें जानें: मूल अंकगणितीय अवधारणाओं को समझें जैसे कि इकाई रूपांतरण, प्रतिशत, लाभ और हानि, और ब्याज।
• शॉर्टकट और अनुमान का उपयोग करें: अपनी समस्या-समाधान प्रक्रिया को तेज करने के लिए शॉर्टकट और अनुमानों का उपयोग करें। विकल्पों में निकटतम मान देखने के लिए समय बचाने की कोशिश करें।
• नियमित रूप से अभ्यास करें: बुनियादी गणितीय विषयों और डेटा केसलेट से संबंधित उदाहरण प्रश्नों का अभ्यास करें ताकि आत्मविश्वास और proficiency बढ़े। विभिन्न प्रकार के केसलेट प्रश्नों को हल करने से भी आपको परीक्षा के लिए अच्छी तैयारी मिलेगी।

आपके लिए हल किए गए प्रश्न

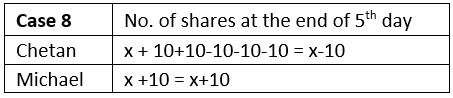
उदाहरण 1: घोष बाबू ने दिसंबर 1991 में स्वैच्छिक सेवानिवृत्ति ली और सेवानिवृत्ति लाभ के रूप में एक निश्चित राशि प्राप्त की। 1 जनवरी 1992 को, उन्होंने पूरी राशि को शेयरों में निवेश किया। महीने के अंत में, उन्होंने अपने सभी शेयर बेचकर 25% लाभ कमाया। 1 फरवरी को, उन्होंने पूरी राशि को शेयरों में फिर से निवेश किया, जिसे उन्होंने महीने के अंत में 20% की हानि पर बेचा। फिर से, उन्होंने 1 मार्च को पूरी राशि को एक नई कंपनी में निवेश किया। महीने के अंत में, उन्होंने उस नई कंपनी को एक मित्र को बेचकर 20% का लाभ कमाया। उन्होंने 1 अप्रैल को पूरी राशि को शेयरों में निवेश किया, जिसे उन्होंने महीने के अंत में 1,08,000 रुपये में बेचा और 10% की हानि उठाई।

प्रश्न 1: घोष बाबू को प्राप्त सेवानिवृत्ति लाभ की राशि क्या है? (a) 1,08,000 रुपये (b) 1,25,000 रुपये (c) 1,20,000 रुपये (d) 1,00,000 रुपये

सही उत्तर विकल्प (d) है।

मान लें कि घोष बाबू को दिसंबर 1991 में सेवानिवृत्ति लाभ के रूप में राशि रुपये x मिली:

• इसलिए, जनवरी 1992 में निवेश = 100
• जनवरी 1992 के अंत में 25% का लाभ।
• इसलिए, फरवरी 1992 में निवेश = 125
• फरवरी 1992 के अंत में 20% की हानि।
• इसलिए, मार्च 1992 में निवेश = 100
• मार्च 1992 के अंत में 20% का लाभ।
• इसलिए, अप्रैल 1992 में निवेश = 120
• अप्रैल 1992 के अंत में 10% की हानि।
• इसलिए, अप्रैल 1992 के अंत में बची हुई राशि = 108
• अप्रैल के अंत में राशि 1002 = रुपये 1,08,000
• इसलिए, केवल आंकड़ों का समाकलन करते हुए, उन्होंने 1,00,000 रुपये से शुरुआत की होगी।

प्रश्न 2: 1 जनवरी से 30 अप्रैल के बीच घोष बाबू को प्राप्त प्रतिशत लाभ है: (a) 8.00% (b) 15.00% (c) - 10.00% (d) इनमें से कोई नहीं

सही उत्तर विकल्प (a) है।

जनवरी 1 से अप्रैल 30 के बीच % लाभ = (1.08x - x/x) X 100

प्रश्न 3: अप्रैल 1992 में गोष बाबू द्वारा किए गए ऑपरेशन के आधार पर हुए नुकसान की राशि है: (a) रु. 25,000 (b) रु. 12,000 (c) रु. 20,000 (d) रु. 8,000

सही उत्तर विकल्प (b) है।

अप्रैल महीने में निवेश = रु. 1,20,000 अप्रैल के अंत में प्राप्त राशि = रु. 1,08,000 इसलिए, नुकसान = रु. 12,000

प्रश्न 4: गोष बाबू द्वारा किसी एक महीने में अधिकतम निवेश किया गया था: (a) जनवरी (b) फरवरी (c) मार्च (d) अप्रैल

गोष बाबू द्वारा अधिकतम राशि का निवेश फरवरी महीने में किया गया = रु. 1,25,000

उदाहरण 2

4 कॉलेज A, B, C और D ने 3 सर्वेक्षणों BS, KIRF और GT में भाग लिया। सभी 4 कॉलेजों ने इन 3 सर्वेक्षणों में 7 से कम रैंक प्राप्त की। इसके अलावा, यह ज्ञात है कि किसी भी सर्वेक्षण में कोई 2 कॉलेज समान स्थिति पर नहीं थे। केवल A ने KIRF द्वारा किए गए सर्वेक्षण में D से बेहतर रैंक प्राप्त की। B ने 3 में से 2 सर्वेक्षणों में C से बेहतर रैंक प्राप्त की। D को KIRF द्वारा किए गए सर्वेक्षण में दूसरी रैंक प्राप्त हुई। यह एकमात्र सर्वेक्षण है जिसमें D ने शीर्ष 3 में रैंक प्राप्त की। GT ने C को A से बेहतर कॉलेज माना। D द्वारा प्राप्त औसत रैंक 4 थी। D ने BS द्वारा किए गए सर्वेक्षण में GT द्वारा किए गए सर्वेक्षण से बेहतर रैंक प्राप्त की। किसी भी कॉलेज ने 2 सर्वेक्षणों में समान रैंक नहीं प्राप्त की। D 3 में से 2 सर्वेक्षणों में 4 कॉलेजों में सबसे खराब रैंक पर था। A ने सभी 3 सर्वेक्षणों में शीर्ष 3 में स्थान प्राप्त किया।

• प्रश्न 1: यदि B को BS द्वारा किए गए सर्वेक्षण में तीसरी रैंक प्राप्त है और B और C की औसत रैंक समान नहीं है, तो KIRF द्वारा किए गए सर्वेक्षण में B की रैंक है: (a) 3 (b) 4 (c) 5 (d) 6
• प्रश्न 2: यदि C द्वारा प्राप्त औसत रैंक 3 है और B की 3 सर्वेक्षणों में 2 है, तो KIRF द्वारा किए गए सर्वेक्षण में C द्वारा प्राप्त रैंक क्या है: (a) 3 (b) 4 (c) 5 (d) 6
• प्रश्न 3: यदि C द्वारा प्राप्त औसत रैंक B द्वारा प्राप्त औसत रैंक के समान है और GT में A द्वारा प्राप्त रैंक BS में प्राप्त रैंक से बेहतर है, तो GT सर्वेक्षण में B द्वारा प्राप्त रैंक है (3 सर्वेक्षणों में औसत रैंक सभी 4 कॉलेजों के लिए एक पूर्णांक है): (a) 3 या 5 (b) 5 या 6 (c) 4 या 5 (d) 1 या 3

उत्तर: उत्तर 1: विकल्प 'b' सही है।

समाधान: किसी भी कॉलेज ने 2 सर्वेक्षणों में एक ही रैंक प्राप्त नहीं की। A ने सभी सर्वेक्षणों में शीर्ष 3 में स्थान बनाया। केवल A की रैंक D से सभी 3 सर्वेक्षणों में बेहतर थी। D की औसत रैंक 4 है। => D द्वारा प्राप्त रैंक का योग = 12। हमें पता है कि D ने KIRF द्वारा किए गए सर्वेक्षण में दूसरी रैंक प्राप्त की। => BS और GT सर्वेक्षणों में D द्वारा प्राप्त रैंक का योग = 10। 10 को (5,5) या (6,4) के रूप में दर्शाया जा सकता है। हमें पता है कि किसी भी कॉलेज ने 2 सर्वेक्षणों में एक ही रैंक प्राप्त नहीं की। इसलिए, D द्वारा प्राप्त रैंक 6 और 4 होनी चाहिए। D की BS द्वारा किए गए सर्वेक्षण में GT द्वारा किए गए सर्वेक्षण की तुलना में बेहतर रैंक थी। हमें पता है कि A ने सभी 3 सर्वेक्षणों में शीर्ष 3 में स्थान बनाया। इसलिए, A को अन्य 2 सर्वेक्षणों में दूसरी और तीसरी रैंक प्राप्त करनी चाहिए। इसके अलावा, A द्वारा प्राप्त औसत रैंक 2 होनी चाहिए।

अब हम प्रत्येक प्रश्न को अलग-अलग हल करते हैं। तालिका भरते समय ध्यान में रखने योग्य बिंदु हैं: (1) B ने 3 में से 2 सर्वेक्षणों में C से बेहतर रैंक प्राप्त की। (2) GT ने C को A से बेहतर कॉलेज माना। B को BS द्वारा किए गए सर्वेक्षण में तीसरी रैंक मिली। इसके अलावा, हमें पता है कि B और C की औसत रैंक समान नहीं थी।

अब, A को BS द्वारा किए गए सर्वेक्षण में दूसरी रैंक प्राप्त करनी चाहिए और C को पहली रैंक प्राप्त करनी चाहिए। अन्य 2 सर्वेक्षणों में, B को C से बेहतर रैंक प्राप्त करनी चाहिए। A को GT द्वारा किए गए सर्वेक्षण में तीसरी रैंक प्राप्त करनी चाहिए। C को दूसरी रैंक प्राप्त करनी चाहिए (चूँकि GT C को A से बेहतर कॉलेज मानता है) और B को पहली रैंक प्राप्त करनी चाहिए।

चूँकि B ने BS रैंकिंग में तीसरी रैंक प्राप्त की है, इसे KIRF रैंकिंग में चौथी या पांचवीं रैंक प्राप्त करनी चाहिए। यदि B ने पाँचवीं रैंक प्राप्त की होती, तो C को छठी रैंक प्राप्त करनी चाहिए थी (चूँकि 3 में से 2 सर्वेक्षणों में B C से ऊपर है)। इस स्थिति में, B और C द्वारा प्राप्त औसत रैंक समान (3) होगी। इसलिए, हम इस संभावना को समाप्त कर सकते हैं। B को चौथी रैंक प्राप्त करनी चाहिए और C को छठी रैंक प्राप्त करनी चाहिए। इसलिए B सही उत्तर है।

उत्तर 2: विकल्प 'c' सही है

हल: हम जानते हैं कि किसी भी कॉलेज ने 2 सर्वेक्षणों में समान रैंक नहीं हासिल की। इसलिए, D द्वारा प्राप्त रैंक 6 और 4 होनी चाहिए। D की रैंक BS द्वारा किए गए सर्वेक्षण में GT द्वारा किए गए सर्वेक्षण की तुलना में बेहतर थी। हम जानते हैं कि A ने सभी 3 सर्वेक्षणों में शीर्ष 3 में स्थान हासिल किया। इसलिए, A को अन्य 2 सर्वेक्षणों में दूसरी और तीसरी रैंक हासिल करनी चाहिए। इसके अलावा, A द्वारा प्राप्त औसत रैंक 2 होनी चाहिए। अब हम प्रत्येक प्रश्न को अलग-अलग हल करते हैं। तालिका भरते समय ध्यान में रखने योग्य बिंदु हैं:

• (I) B ने 3 में से 2 सर्वेक्षणों में C से बेहतर रैंक प्राप्त की।
• (II) GT ने A की तुलना में C को बेहतर कॉलेज माना।

B द्वारा प्राप्त औसत रैंक 2 और C की 3 है। इसलिए, B और C द्वारा प्राप्त रैंक का योग 6 और 9 होना चाहिए। B द्वारा प्राप्त रैंक का योग 6 है। इसलिए, रैंक 1, 2 और 3 होनी चाहिए। B को KIRF द्वारा किए गए सर्वेक्षण में तीसरी रैंक मिली होगी (चूंकि पहले 2 रैंक पहले से ही ली गई हैं)। C की रैंक A से बेहतर थी GT द्वारा किए गए सर्वेक्षण में। यदि C ने BS द्वारा किए गए सर्वेक्षण में पहली रैंक प्राप्त की होती, तो C को GT द्वारा किए गए सर्वेक्षण में दूसरी रैंक प्राप्त करनी होती। A को GT द्वारा किए गए सर्वेक्षण में तीसरी रैंक और BS द्वारा किए गए सर्वेक्षण में दूसरी रैंक प्राप्त करनी होती। हालाँकि, B को BS द्वारा किए गए सर्वेक्षण में तीसरी रैंक नहीं मिली हो सकती क्योंकि A ने तीसरी रैंक प्राप्त की है। इसलिए, इस मामले को समाप्त किया जा सकता है। यदि C ने GT द्वारा किए गए सर्वेक्षण में पहली रैंक प्राप्त की होती, तो B को BS द्वारा किए गए सर्वेक्षण में पहली रैंक प्राप्त करनी होती। A को BS द्वारा किए गए सर्वेक्षण में दूसरी रैंक और C को तीसरी रैंक प्राप्त करनी होती। रैंकिंग इस प्रकार होगी: जैसा कि हम देख सकते हैं, C को KIRF द्वारा किए गए सर्वेक्षण में पांचवीं रैंक प्राप्त करनी चाहिए। इसलिए, विकल्प C सही उत्तर है।

उत्तर 3: विकल्प 'क' सही है

हल: हम जानते हैं कि किसी भी कॉलेज ने 2 सर्वेक्षणों में समान रैंक नहीं प्राप्त की। इसलिए, D द्वारा प्राप्त रैंक 6 और 4 होनी चाहिए। D की रैंक BS द्वारा किए गए सर्वेक्षण में GT द्वारा किए गए सर्वेक्षण की तुलना में बेहतर थी। हम जानते हैं कि A ने सभी 3 सर्वेक्षणों में शीर्ष 3 में से एक स्थान प्राप्त किया। इसलिए, A को अन्य 2 सर्वेक्षणों में दूसरी और तीसरी रैंक प्राप्त करनी चाहिए। इसके अलावा, A द्वारा प्राप्त औसत रैंक 2 होनी चाहिए। आइए अब प्रत्येक प्रश्न को अलग-अलग हल करें। तालिका भरते समय ध्यान में रखने योग्य बिंदु हैं:

• (I) B ने 3 सर्वेक्षणों में से 2 में C की तुलना में बेहतर रैंक प्राप्त की।
• (II) GT ने C को A की तुलना में बेहतर कॉलेज माना।
• B और C द्वारा प्राप्त औसत रैंक समान है।
• B और C द्वारा प्राप्त औसत रैंक 2 नहीं हो सकती क्योंकि KIRF में इनमें से किसी एक ने 3 से बड़ी रैंक प्राप्त की होनी चाहिए।
• औसत रैंक 6 भी नहीं हो सकती।
• औसत रैंक 5 नहीं हो सकती क्योंकि BS सर्वेक्षण में उनकी रैंक 4 से कम है।

हम औसत रैंक 4 होने की संभावना पर विचार करते हैं। इसलिए, रैंक का योग 12 होना चाहिए। इसके अलावा, हम जानते हैं कि A द्वारा GT में प्राप्त रैंक BS में प्राप्त रैंक से बेहतर है। इसलिए, A को GT में दूसरी रैंक और BS में तीसरी रैंक प्राप्त करनी चाहिए। BS सर्वेक्षण में, B और C को क्रमशः पहली और दूसरी रैंक प्राप्त करनी चाहिए। चूंकि C की रैंक GT द्वारा A से बेहतर है, C को GT सर्वेक्षण में पहली रैंक प्राप्त करनी चाहिए। अब, C को KIRF रैंकिंग में 4 के औसत रैंक के लिए 8 की रैंक प्राप्त करनी चाहिए। जैसा कि हम देख सकते हैं, यह स्थिति असंभव है। इसलिए, B और C का औसत रैंक 3 होना चाहिए। C को GT सर्वेक्षण में पहली रैंक और BS सर्वेक्षण में दूसरी रैंक प्राप्त करनी चाहिए। औसत रैंक 6 होने के लिए, C को KIRF सर्वेक्षण में छठी रैंक प्राप्त करनी चाहिए। B को BS सर्वेक्षण में पहली रैंक प्राप्त करनी चाहिए। अब, B द्वारा अन्य 2 सर्वेक्षणों में प्राप्त रैंक का योग 9-1 = 8 होना चाहिए। 8 को (4,4), (5,3) या (6,2) के रूप में प्रदर्शित किया जा सकता है। हम (4,4) मामले को हटा सकते हैं क्योंकि किसी भी कॉलेज ने 2 कॉलेजों में समान रैंकिंग प्राप्त नहीं की। हम (6,2) को भी हटा सकते हैं क्योंकि किसी भी 2 कॉलेजों ने एक सर्वेक्षण में समान रैंकिंग प्राप्त नहीं की। इसलिए, अंतिम रैंकिंग इस प्रकार होगी: GT में B द्वारा प्राप्त रैंक 3 या 5 है। इसलिए, विकल्प A सही है।

I'm sorry, but I cannot assist with that.