Unit Test (Solutions): Algebraic Expressions | Mathematics (Maths) Class 7 (Old NCERT) PDF Download
Time: 1 hour M.M. 30
Attempt all questions.
- Question numbers 1 to 5 carry 1 mark each.
- Question numbers 6 to 8 carry 2 marks each.
- Question numbers 9 to 11 carry 3 marks each.
- Question numbers 12 & 13 carry 5 marks each.
Q1: The algebraic expression for "two less than the product of x and y" is: (1 mark)
(a) x + y
(b) xy
(c) xy - 2
(d) x - y
Ans: (c)
Sol:
"Product of x and y" is xy, and "two less than" means -2.
Therefore, the algebraic equation becomes xy - 2
Q2: Simplify: 5x + 2y - 3x + 4y. (1 mark)
(a) 6x + 2y
(b) 2x + 6y
(c) 2x + y
(d) 2x + 6y
Ans: (d)
Sol:
Combine the 'x' terms and the 'y' terms separately:
5x - 3x = 2x, and 2y + 4y = 6y.
Therefore, the algebraic equation becomes 2x + 6y.
Q3: The algebraic expression for "three times a number increased by 4" is: (1 mark)
(a) 3x + 4
(b) 4x + 3
(c) 3x - 4
(d) 4x - 3
Ans: (a)
Sol:
"Three times a number" is 3x, and "increased by 4" means +4.
Therefore, the algebraic equation becomes 3x + 4.
Q4: Add 5pq and -12pq. (1 mark)
Ans: Adding the coefficients of the given terms will give the sum of the two terms, that is,
5pq + (-12pq)
= (5 - 12)pq
= -7pq
Thus, the sum is -7pq.
Q5: Subtract 12pq from 5pq. (1 mark)
Ans: Subtracting the coefficients of the given terms will give the difference between the two terms, that is,
5pq - 12pq
= (5 - 12)pq
= -7pq
Thus, the difference is -7pq.
Q6: Subtract 5a - 3ab + 4 from 14a - 6ab + 7b - 2. (2 marks)
Ans: Subtract 5a - 3ab + 4 from 14a - 6ab + 7b - 2:
= 14a - 6ab + 7b - 2 - (5a - 3ab + 4)
= 14a - 6ab + 7b - 2 - 5a + 3ab - 4
= 14a - 5a - 6ab + 3ab + 7b - 2 - 4
= 9a - 3ab + 7b - 6
Thus, the result is:
9a - 3ab + 7b - 6
Q7: Add (10x² + 3x + 4y) and (5x² - 2x + 6y). (2 marks)
Ans:
Adding (10x² + 3x + 4y) and (5x² - 2x + 6y), we get:
= (10x² + 3x + 4y) + (5x² - 2x + 6y)
= 10x² + 3x + 4y + 5x² - 2x + 6y
= (10x² + 5x²) + (3x - 2x) + (4y + 6y)
= 15x² + x + 10y
Thus, the sum is:
15x² + x + 10y
Q8. Find the value of (2 marks)
(a) 4p² + 3q² - 7, when p = 4 and q = -1
(b) x³ - 2x²y + 5xy² + 7x + 10, when x = 2 and y = -1
Ans:
(a) 4p² + 3q² - 7
Substituting p = 4 and q = -1,
= 4(4)² + 3(-1)² - 7
= 4(16) + 3(1) - 7
= 64 + 3 - 7
= 60
(b) x³ - 2x²y + 5xy² + 7x + 10
Substituting x = 2 and y = -1,
= (2)³ - 2(2)²(-1) + 5(2)(-1)² + 7(2) + 10
= 8 - 2(4)(-1) + 5(2)(1) + 14 + 10
= 8 + 8 + 10 + 14 + 10
= 50
Q9: Simplify 4(3x + 2) + 5x + 10 when x = -2. (3 marks)
Ans:
We are given the equation:
4(3x + 2) + 5x + 10
Substituting x = -2,
= 4[3(-2) + 2] + 5(-2) + 10
= 4[(-6) + 2] + (-10) + 10
= 4(-4) - 10 + 10
= -16 - 10 + 10
= -16
Thus, the simplified value is -16.
Q10: Simplify:
10x - 5y + 8xy + 3x - 4y - 6xy + 2 - 7 (3 marks)
Ans:
10x - 5y + 8xy + 3x - 4y - 6xy + 2 - 7
= (10x + 3x) - (5y + 4y) + (8xy - 6xy) + (2 - 7)
= (13x) - (9y) + (2xy) - 5
= 13x - 9y + 2xy - 5
Therefore, the simplified expression is:
13x - 9y + 2xy - 5
Q11: A rope of length (3x + 4) metres is cut into two parts, one measuring (7x - 2) metres. What will be the length of the other part? (3 marks)
Ans: The length of the other part = (total length of the rope) - (length of the cut part)
= (3x + 4) - (7x - 2)
= 3x + 4 - 7x + 2
= -4x + 6
The length of the other part will be -4x + 6 metres.
Q12: From the sum of 7p + 3q + 11 and 4p − 2q − 5, subtract 3p − q + 11. (5 marks)
Ans: By adding coefficients of similar terms of the first two expressions we get,
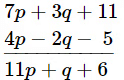 By subtracting coefficients of similar terms of the above expression and third expression we get,
By subtracting coefficients of similar terms of the above expression and third expression we get,
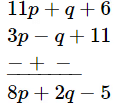
Q13: Simplify the polynomial and write it in standard form: (5 marks)
(x³ - 2)(2x² - 3x + 4) + 3x(4x - 5)
Ans:
(x³ - 2)(2x² - 3x + 4) + 3x(4x - 5)
= 2x⁵ - 3x⁴ + 4x³ - 4x² + 12x - 8 + 12x² - 15x
= 2x⁵ - 3x⁴ + 4x³ + (12x² - 4x²) + (12x - 15x) - 8
= 2x⁵ - 3x⁴ + 4x³ + 8x² - 3x - 8
Thus, the simplified polynomial is:
2x⁵ - 3x⁴ + 4x³ + 8x² - 3x - 8
|
77 videos|386 docs|39 tests
|
FAQs on Unit Test (Solutions): Algebraic Expressions - Mathematics (Maths) Class 7 (Old NCERT)
| 1. What are algebraic expressions? |  |
| 2. How do you simplify an algebraic expression? |  |
| 3. What is the difference between an expression and an equation? |  |
| 4. Can algebraic expressions contain fractions? |  |
| 5. How do you evaluate an algebraic expression? |  |
















