Practice Test: Data Sufficiency | Data Insights for GMAT PDF Download
Q1. Company Q has 18,000 employees, 40 percent of whom are married. What percent of the employees are married and have been with the company for more than 15 years?
(1) The number of employees who are married is 3 times the number of unmarried employees who have been with the company for no more than 15 years.
(2) The number of married employees who have been with the company for more than 15 years is 4 times the number of married employees who have been with the company for no more than 15 years.
(a) Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
(b) Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
(c) BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
(d) EACH statement ALONE is sufficient to answer the question asked.
(e) Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Ans: Option B is correct.
Sol: From the stem, we can make
Total Employees =18000 .Married Emp =7200. unmarried Emp= 10800.
Question : Married Employees > 15years?
- Statement 1: It does not provide any information about married employees >15 years. Insufficient.
- Statement 2: From this we can deduce that 4x+x= 7200 (Where x is the unknown variable). Upon solving we can find number of married employees >15 years. Sufficient.
Thus, Option B is correct.
Q2: Given that n is an integer, is n — 1 divisible by 3?
(1) n2 + n is not divisible by 3
(2) 3n +5 ≥ = k+8 , where k is a positive multiple of 3
(a) Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
(b) Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
(c) BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
(d) EACH statement ALONE is sufficient.
(e) Statements (1) and (2) TOGETHER are NOT sufficient.
Ans: (a)
Sol: (1) n2 + n is not divisible by 3 → n(n+1) is not divisible by 3 → neither n nor n+1 is divisible by 3.
Now, n-1, n and n+1 are three consecutive integers, thus one of them must be divisible by 3,
so if n and n+1 are NOT, then n-1 must be. Sufficient.
(2) 3n +5 ≥ = k + 8 , where k is a positive multiple of 3. Not sufficient.
Q3: If x, y and z are positive integers such that x4y3 = z2, is x9 - y6 odd?
(1) 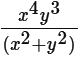 can be written in the form 4k+3, where k is a positive integer
can be written in the form 4k+3, where k is a positive integer
(2) z = x + y
(a) Statement (1) alone is sufficient, but statement (2) alone is not sufficient.
(b) Statement (2) alone is sufficient, but statement (1) alone is not sufficient.
(c) Both statements together are sufficient, but neither alone is sufficient.
(d) Each statement alone is sufficient.
(e) Statements (1) and (2) together are not sufficient.
Ans: (d)
Sol: Step-I: Given Info
We are given three positive integers x, y and z such that x4y3 = z2, and we are asked to find if x9 – y6 is odd
Step-II: Interpreting the Question Statement
For the expression x9 – y6 to be odd, both the expressions need to be of opposite even/odd nature i.e. one has to be odd and another has to be even (as even- odd = odd or odd-even = odd). Since the even/odd nature of x9 would have the same even/odd nature as x and even/odd nature of y6 would be the same even/odd nature as y, if we can determine the similar or opposite nature of x, y we can determine the even/odd nature of x9–y6.
Step-III: Statement-I
We are told that 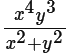 can be written in the form 4k + 3, where k is a positive integer. We observe here that a fraction has been simplified to an odd number (as 4k is always even and even + odd = odd) which would imply that both the numerator and the denominator are either even or odd.
can be written in the form 4k + 3, where k is a positive integer. We observe here that a fraction has been simplified to an odd number (as 4k is always even and even + odd = odd) which would imply that both the numerator and the denominator are either even or odd.
Hence, we can say that the product of x and y and the sum of x and y have the same even/odd nature.
This is possible only if x, y are both even. Since, we have determined the similar nature of x, y we can say with certainty that expression x9 –y6 is always even.
Hence, statement-I is sufficient to answer the question.
Step-IV: Statement-II
Statement-II tells us that z = x + y , we know that z is expressed as a product of x and y. Since the product of x, y have the same even/odd nature as that of the sum of x and y, we can say with certainty that x, y are both even. Hence, statement-II is sufficient to answer the question.
Step-V: Combining Statements I & II
Since, we have a unique answer from Statement- I & II we don’t need to be combine Statements- I & II.
Hence, the correct answer is Option D
Q4: Color X ink is created by blending red, blue, green, and yellow inks in the ratio 6 : 5 : 2: 2. What is the number of liters of green ink that was used to create a certain batch of color X ink?
(1) The amount of red ink used to create the batch is 2 liters more than the amount of blue ink used to create the batch.
(2) The batch consists of 30 liters of color X ink.
(a) Statement (1) alone is sufficient, but statement (2) alone is not sufficient.
(b) Statement (2) alone is sufficient, but statement (1) alone is not sufficient.
(c) Both statements together are sufficient, but neither alone is sufficient.
(d) Each statement alone is sufficient.
(e) Statements (1) and (2) together are not sufficient.
Ans: (d)
Sol: Let the number of liters of red ink be = 6*x
blue ink be = 5*x
green ink be = 2*x
yellow ink be = 2*x
Statement 1 says , 6*x - 5*x = 2
x = 2
So the number of liters of green ink = 2 *2 = 4 liters
Statement 2 says , 15 *x = 30
x = 2
So the number of liters of green ink = 2 *2 = 4 liters
Each statement is sufficient.
Option D is the answer.
Q5: Twelve jurors must be picked from a pool of n potential jurors .If m of the potential jurors are rejected by the defense counsel and the prosecuting attorney ,how many different possible juries could be picked from the remaining potential jurors?
(1) If one less potential juror had been rejected, it would be possible to create 13 different juries.
(2) n = m + 12
(a) Statement (1) alone is sufficient, but statement (2) alone is not sufficient.
(b) Statement (2) alone is sufficient, but statement (1) alone is not sufficient.
(c) Both statements together are sufficient, but neither alone is sufficient.
(d) Each statement alone is sufficient.
(e) Statements (1) and (2) together are not sufficient.
Ans: (d)
Sol: Essentially, there is an (n-m) pool of jurors to select a group of 12 from. As a result, the number of possible juries is equivalent to (n - m)C12, or: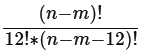
For simplicity's sake, let's set X = n - m (the pool of jurors available after processing by the defense counsel). As a result the number of possible juries is equivalent to: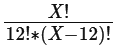
Statement 1: If one less potential juror had been rejected ,it would be possible to create 13 different juries:
As a result, X increases to X + 1: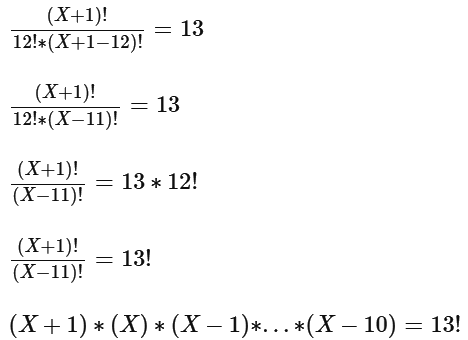
Therefore, by using our understanding of factorials, we can determine X (or n-m) to be 12. The answer to the original question then becomes 1, and Statement 1 is proven to be sufficient.
Statement 2: n=m+12:
Rearranging the equation sets n-m = 12, which is enough to show that the answer to the original question is 1 possible jury, and Statement 2 also proves to be sufficient.
Therefore, both statements are sufficieint by themselves, and the answer is D.
Q6: 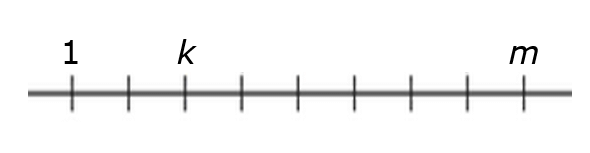 If the tick marks shown on the line above are equally spaced, what is the value of m?
If the tick marks shown on the line above are equally spaced, what is the value of m?
(1) k = 13/11
(2) (k + m)/3 + 1/33 = 1
(a) Statement (1) alone is sufficient, but statement (2) alone is not sufficient.
(b) Statement (2) alone is sufficient, but statement (1) alone is not sufficient.
(c) Both statements together are sufficient, but neither alone is sufficient.
(d) Each statement alone is sufficient.
(e) Statements (1) and (2) together are not sufficient.
Ans: (d)
Sol: If "d" is the spacing between tick marks, then k = 1 + 2d, and m = 1 + 8d. So we really only have one unknown, and any equation that lets us find "d' will be sufficient. Statement 1 tells us that d = 1/11, so it is sufficient. Substituting into Statement 2, we find
(k + m)/3 + 1/33 = 1
k + m + 1/11 = 3
(1 + 2d) + (1 + 8d) + 1/11 = 3
2 + 10d + 1/11 = 3
10d = 10/11
d = 1/11
and Statement 2 is sufficient.
Of course, since this is DS, you can stop solving the equation in Statement 2 as soon as you notice you'll get a numerical answer for d.
Q7: When a certain drug was administered to a group of patients, some patients showed improvement and some patients experienced side effects. If at least 10 patients experienced side effects and 60 percent of the patients who showed improvements also experienced side effects, did more patients in the group show improvement than experience side effects?
(1) 90 percent of the patients in the group showed improvement.
(2) 90 percent of the patients in the group who experienced side effects also showed improvement.
(a) Statement (1) alone is sufficient, but statement (2) alone is not sufficient.
(b) Statement (2) alone is sufficient, but statement (1) alone is not sufficient.
(c) Both statements together are sufficient, but neither alone is sufficient.
(d) Each statement alone is sufficient.
(e) Statements (1) and (2) together are not sufficient.
Ans: (d)
Sol: (1) 90 percent of the patients in the group showed improvement.
Let us find the maximum possible number of those who could have had side effects.
We know that 60% of these 90% showed side effects. To maximize, let is take the remaining 100-90 or 10% patients who did not show improvement showed side effects too. Thus, total = 10% + 60% of 90% = 10% + 54% or 64%.
64%<90% or y<x.
Sufficient
(2) 90 percent of the patients in the group who experienced side effects also showed improvement.
So, this is the common group in terms of y, that is 90% of y belong to overlap.
But we also know that 60 percent of the patients who showed improvements also experienced side effects,so, 60% of x belong to overlap. Also, the overlap space cannot be different.
This gives 90% of y = 60% of x or 0.9y = 0.6x or 1.5y=x
Hence x>y Sufficient
Q8: Machines X and Y can work at their respective constant rates to manufacture a certain production unit. If both are working alone, then the time taken by machine Y is what percentage more/less than that of machine X?
(1) Machines X and Y, working together, complete a production order of the same size in two-thirds the time that machine Y, working alone, does.
(2) Machine Y, working alone, fills a production order of twice the size in 6 hrs.
(a) Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
(b) Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
(c) BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
(d) EACH statement ALONE is sufficient.
(e) Statements (1) and (2) TOGETHER are NOT sufficient.
Ans: (a)
Sol: Given: Machine X and Y work at their respective constant rates to manufacture a certain production unit
To find: When both machines are working alone, the time taken by machine Y is what percentage more/less than that of machine X
Approach and Working:
If we assume the time taken by machine X and Y individually to complete the work is t1 and t2 respectively, then
Time t2 is more than time t1 by (as a percentage) = 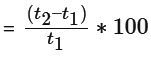
This can be written as = 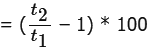
[Note that if t2 is less than t1, then the above expression will be equal to (1 - t2/t1)* 100
Hence, if we can find the value of the ratio t2/t1, we can find out the required percentage
Analysing Statement 1
As per the information given in statement 1, Machines X and Y, working together, complete a production order of the same size in two-thirds the time that machine Y, working alone, does.
The time taken by both of them together to complete the job = 
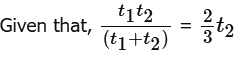
Simplifying, we can write t2/t1 = 2/1
Hence, statement 1 is sufficient enough to answer the question
Analysing Statement 2
As per the information given in statement 2, Machine Y, working alone, fills a production order of twice the size in 6 hrs
From this statement, we can say t2 = 3 hours
But we cannot conclude any relationship between t1 and t2
Hence, statement 2 is not sufficient to answer the question
Hence, the correct answer is option A.
|
24 videos|28 docs|21 tests
|
FAQs on Practice Test: Data Sufficiency - Data Insights for GMAT
| 1. What is Data Sufficiency in the context of the CAT exam? |  |
| 2. How should I approach Data Sufficiency questions in the CAT exam? |  |
| 3. Are there specific strategies to improve performance in Data Sufficiency questions? |  |
| 4. How important is Data Sufficiency in the overall CAT exam scoring? |  |
| 5. Can I use a calculator for Data Sufficiency questions on the CAT exam? |  |
















