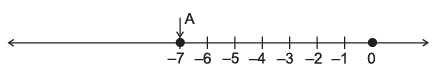Class 6 Mathematics: Sample Paper Solutions- 5 | Sample Papers For Class 6 PDF Download
General Instructions
All questions are compulsory.
- Section A comprises 12 questions carrying 1 mark each.
- Section B comprises 10 questions carrying 2 marks each.
- Section C comprises 8 questions carrying 3 marks each.
- Section D comprises 2 questions carrying 5 marks each.
Q1: How many lines of symmetry does a regular octagon have? (1 mark)
(a) 3
(b) 4
(c) 8
(d) 6
Ans: (c)
Q2: The perimeter of a rectangle is 24 cm. If the length is 8 cm, what is the width? (1 mark)
(a) 5 cm
(b) 8 cm
(c) 4 cm
(d) 6 cm
Ans: (c)
Q3: In the fraction 7/10, what is 7 called? (1 mark)
(a) Denominator
(b) Numerator
(c) Quotient
(d) Whole number
Ans: (b)
Q4: Convert the improper fraction 13/5 into a mixed fraction. (1 mark)
(a) 2 3/5
(b) 3 2/5
(c) 2 1/5
(d) 2 2/5
Ans: (a)
Q5: The temperature in a city is 3°C in the morning. By noon, it rises by 6°C. What is the temperature at noon? (1 mark)
(a) 10°C
(b) 5°C
(c) 9°C
(d) 6°C
Ans: (a)
Q6: Add the following fractions using Brahmagupta's method: (1 mark)
4/7 + 3/7
(a) 7/7
(b) 1
(c) 2/7
(d) 3/7
Ans: (a)
Q7: Which of the following pairs of numbers are co-prime? (1 mark)
(a) 8 and 16
(b) 18 and 24
(c) 5 and 12
(d) 14 and 28
Ans: (c)
Q8: What is a bar graph? (1 mark)
(a) A graph that uses pictures or objects to represent data
(b) A graph that uses bars to represent data
(c) A mathematical operation
(d) A type of chart used to find averages
Ans: (b)
Q9: A figure has rotational symmetry if it can be rotated by an angle less than __ and still look the same. (1 mark)
(a) 120°
(b) 180°
(c) 360°
(d) 90°
Ans: (c)
Q10: Where can fractions be represented visually? (1 mark)
(a) On a number line
(b) In a bar graph
(c) Only in decimal form
(d) On a clock
Ans: (a)
Q11: Find the missing number in the pattern: (1 mark)
150, 140, 130, __, 110
(a) 120
(b) 125
(c) 115
(d) 105
Ans: (a)
Q12: An acute angle is always: (1 mark)
(a) Less than 90°
(b) Equal to 90°
(c) More than 90° but less than 180°
(d) More than 180°
Ans: (a)
Q13: Neha is arranging chairs in a square pattern. The first row has 1 chair, the second row has 4 chairs, the third row has 9 chairs, and the fourth row has 16 chairs. If she continues this pattern, how many chairs will be in the fifth row? (2 marks)
Ans: The pattern increases by consecutive perfect squares:
1st row = 1² = 1
2nd row = 2² = 4
3rd row = 3² = 9
4th row = 4² = 16
5th row = 5² = 25
The fifth row will have 25 chairs.
Q14: What is the sum of the smallest and largest 5-digit palindrome? What is their difference? (2 marks)
Ans: The smallest 5-digit palindrome = 10001
The largest 5-digit palindrome = 99999Sum = 10001 + 99999 = 110000
Difference = 99999 - 10001 = 89998
Q15: Write two equivalent fractions for 5/8. (2 marks)
Ans: Here,
5/8 → 5 × 2 / 8 × 2 = 10/16
5/8 → 5 × 3 / 8 × 3 = 15/24Here,
10/16, 15/24 are equivalent fractions of 5/8.
Q16: A square-shaped garden has a side length of 12 m. Find its area. (2 marks)
Ans: Area of a square = side × side
= 12 × 12
= 144 sq. m
Q17: The length of a rectangular park is 50 m and its area is 650 m2. Find its breadth. (2 marks)
Ans: Length=50m
Area=650 m
So, According to the question:
Area of rectangle= Length x Breadth
650=50 x Breadth=50 x Breadth=650
Breadth=650/50
=Breadth=13m
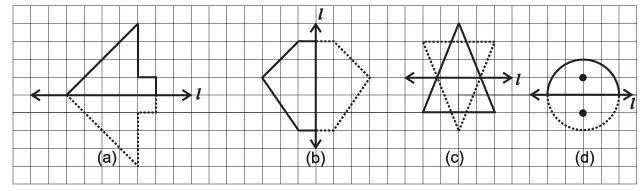
Q18: In the following figures, l is the line of symmetry. Complete the diagram to make it symmetric. (2 marks)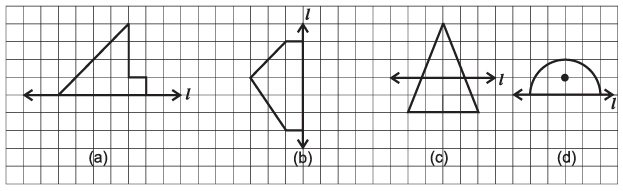
Ans:
Q19: Consider the first ten capital letters of English alphabet, list among them the letters which have :
(i) Vertical lines of symmetry (e.g. A)
(ii) Horizontal lines of symmetry (e.g. B)
(iii) No lines of symmetry (e.g. F)
(iv) Both-vertical and horizontal lines of symmetry (e.g. H)
Ans:
(i) A, H, I
(ii) B, C, D, E, H, I
(iii) F, G, J
(iv) H, I
Q20: Is the first number divisible by the second? Use prime factorization. (2 marks)
(a) 240 and 60
Ans: The prime factorization of 240 is 2 × 2 × 2 × 2 × 3 × 5, and the prime factorization of 60 is 2 × 2 × 3 × 5.
Since 240 has all the factors of 60, it is divisible by 60.
Yes, 240 is divisible by 60.
(b) 1024 and 32
Ans: The prime factorization of 1024 is 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2, and the prime factorization of 32 is 2 × 2 × 2 × 2 × 2.
Since 1024 has all the factors of 32, it is divisible by 32.
Yes, 1024 is divisible by 32.
Q21: A rectangular playground is 600 m long and 250 m wide. If the cost of painting the boundary lines is ₹10 per 100 sq. m, what is the total cost to paint the entire boundary? (3 marks)
Ans: Here, length = 600 m and width = 250 m
Hence, the area of the playground = length × width
= 600 × 250
= 1,50,000 sq. mNow, the cost of painting 100 sq. m = ₹10
Total cost = (10/100) × 150000
= ₹15,000
Q22: A strip of width 4 m is cut out all round from a rectangular sheet of paper with dimensions 60 m × 40 m. Find the area of the strip cut out and the area of the remaining sheet. (3 marks)
Ans: Given that,
Length of the sheet = 60 m
Breadth of the sheet = 40 m
Area of the sheet = 60 × 40 = 2400 m²A strip of width 4 m is cut out all round from the sheet.
Let that form a rectangle PQRS.
Length of the rectangle PQRS = 60 – 4 – 4 = 60 – 8 = 52 m
Breadth of the rectangle = 40 – 4 – 4 = 40 – 8 = 32 mArea of the rectangle PQRS (Area of remaining sheet) = 52 × 32 = 1664 m²
Area of the strip cut out = Area of sheet – Area of PQRS
= 2400 – 1664
= 736 m²∴ The area of the strip cut out = 736 m².
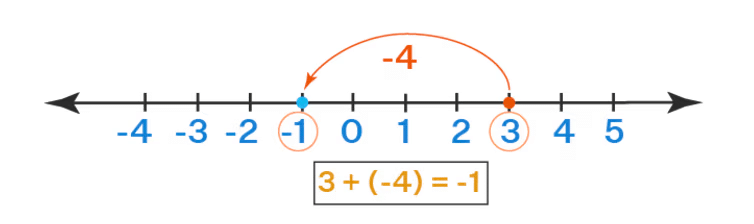
Q23: Represent the following numbers/expressions on a number line? (3 marks)
(i) –7
(ii) 3+ (-4)
(iii) 4 + 6
Ans:
(i)
(ii)
(iii)
Q24: Enter the correct symbol >, =, < in the following : (3 marks)
(i) (–7) _________ (2)
(ii) 7 _________ (–12)
(iii) 0 _________ (–2)
Ans:
(i) <
(ii) >
(iii) >
Q25: Put the following set of fractions in descending order :
(i) 15, 35, 135, 95, 125
(ii) 37, 311, 32, 35, 310
Ans:
(i) Since the denominators are the same we will compare the numerators, then the order becomes :
135 > 125 > 95 > 35 > 15
(ii) The smaller the denominator, the larger the fraction:
32 > 35 > 37 > 310 > 311
Q26: Find the number of square tiles required to cover the floor of a room whose length is 4 m and width 3 m, if each square tile is of side 0.2 m. (3 marks)
Ans: To find the number of square tiles required to cover the floor of a room, we need to first determine the area of the room in square meters. The area of a rectangle is given by the formula:
Area = Length x Width
In this case, the length of the room is 4 m and the width is 3 m, so the area of the room is 4 x 3 = 12 sq m.
Next, we need to determine the area of a single square tile. The area of a square is given by the formula:
Area = Side X 2
In this case, the side of the square tile is 0.2 m, so the area of a single tile is 0.2 X 2 = 0.04 sq m.
To find the number of tiles required to cover the floor of the room, we can divide the area of the room by the area of a single tile:
12 sq m / 0.04 sq m = 300 tiles
Therefore, the number of square tiles required to cover the floor of the room is 300 tiles.
Q27: The temperature in a city at 7 AM was 5°C. Due to a heatwave, the temperature rose by 8°C by 11 AM. Later in the afternoon, as a cloud cover appeared, the temperature dropped by 4°C. By night, it again rose by 3°C. (3 marks)
(A) What was the temperature at 11 AM?
(B) What was the temperature in the afternoon?
(C) What was the temperature at night?
Ans:
(A) At 11 AM:
5 + 8 = 13
The temperature was 13°C.(B) In the afternoon:
13 - 4 = 9
The temperature was 9°C.(C) At night:
9 + 3 = 12
The temperature was 12°C.
Q28: On the number line mark the following numbers: 5, 0, -3, -9 (5 marks)
Ans:
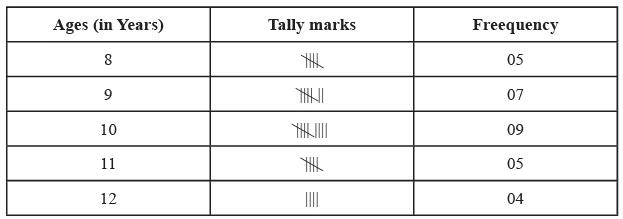
Q29: Reena collected the data for the ages (in years) of her hobby class group and she recorded the findings in the manner shown below: (5 marks)
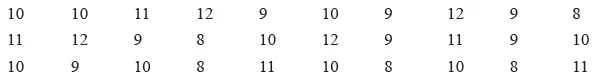
Represent the above data using tally marks in the table below :
| Ages (in years) | Tally Marks | Frequency |
| 8 | 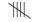 | 05 |
| 9 | ||
| 10 | ||
| 11 | ||
| 12 |
(i) Find the age that appeared maximum number of times?
(ii) Find the ages that appeared equal number of times.
(iii) How many children are below 11 years?
(iv) How many children are of 10 years or above?
Ans:
(i) The age that appeared maximum number of times is 10 years.
(ii) 8 years & 11 years of age appeared equal number of times i.e. 5 times.
(iii) The total number of children below 11 years are 5 + 7 + 9 = 21
(iv) The total number of children that are of 10 years and above are 9 + 5 + 4 = 18
FAQs on Class 6 Mathematics: Sample Paper Solutions- 5 - Sample Papers For Class 6
| 1. What subjects are typically included in the Class 6 exam? |  |
| 2. How can students prepare effectively for the Class 6 exam? |  |
| 3. What is the importance of sample question papers for Class 6 students? |  |
| 4. Are there any specific tips for answering Mathematics questions in the Class 6 exam? |  |
| 5. How can parents support their children during the Class 6 exam preparation? |  |