Cheatsheet: Percentage | Cheatsheets for Bank Exams PDF Download
| Table of contents |

|
| Introduction |

|
| Theory |

|
| Formulas |

|
| Tips & Tricks |

|
| Conclusion |

|
Introduction
Percentages are a fundamental concept in mathematics and everyday life, used to express proportions, compare quantities, and analyze data. The term "percent" means "per hundred," and it is denoted by the symbol %. Understanding percentages is essential for financial calculations, statistics, discounts, and many real-world applications.
Theory
A Percentage represents a fraction with a denominator of 100. For example:
50% means 50/100 or ½.
25% means 25/100 or ¼.
Percentages are used to:
Compare quantities.
Calculate increases or decreases.
Determine proportions (e.g., tax, interest, discounts).
Formulas
1. Basic Percentage Formula
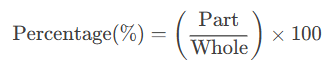 Example:
Example:
If 20 out of 50 students passed a test, the percentage of students who passed is: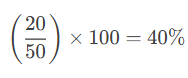
2. Finding the Part (Given Whole and Percentage)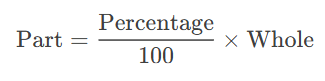
Example:
What is 30% of 200?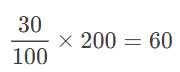
3. Finding the Whole (Given Part and Percentage)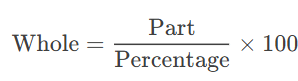
Example:
If 15 is 25% of a number, what is the number?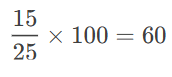
4. Percentage Increase/Decrease 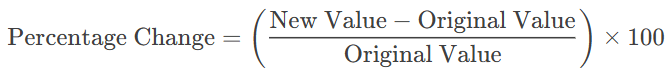
Example:
If a product’s price increases from $50 to $65, the percentage increase is: 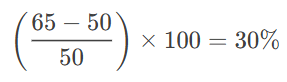
5. Successive Percentage Change
If a value changes by a% and then by b%, the net percentage change is: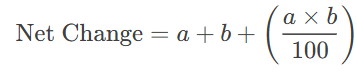
Example:
If a number increases by 10% and then decreases by 20%, the net change is:
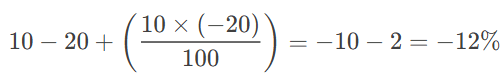
Tips & Tricks
Convert Fractions & Decimals to Percentages:
Fraction → %: Multiply by 100 (e.g., 3/4 = 0.75 = 75% ).
Decimal → %: Shift decimal two places right (e.g., 0.6 = 60%).
Quick Calculations:
50% of X = X/2
25% of X = X/4
10% of X = X/10 (Move decimal one place left).
Reverse Percentages:
If Y is P% of a number, the number is (Y×100)/P.
Discounts & Markups:
Final Price = Original Price × (1 ± Discount%/100)
Conclusion
Percentages are a versatile tool in mathematics, finance, and daily life. Mastering the basic formulas and shortcuts can simplify calculations involving growth rates, discounts, interest, and data analysis. Practice applying these concepts to real-world problems for better understanding.
FAQs on Cheatsheet: Percentage - Cheatsheets for Bank Exams
| 1. What is the basic formula to calculate a percentage? |  |
| 2. How can I increase my speed in solving percentage problems for bank exams? |  |
| 3. What are some common percentage problems that appear in bank exams? |  |
| 4. Can you explain how to find the percentage increase between two numbers? |  |
| 5. What tips can help in understanding the concept of percentage better? |  |















