Cheatsheet: Quadratic Equation | Cheatsheets for Bank Exams PDF Download
| Table of contents |

|
| Introduction |

|
| Theory |

|
| Important Formulas |

|
| Tips for Solving Quadratic Equations Quickly in Bank Exams |

|
| Conclusion |

|
Introduction
A Quadratic Equation is a second-degree polynomial equation of the form: ax² + bx + c = 0
Where:
a, b, and c are constants, and a ≠ 0.
The solutions of a quadratic equation are called the roots of the equation.
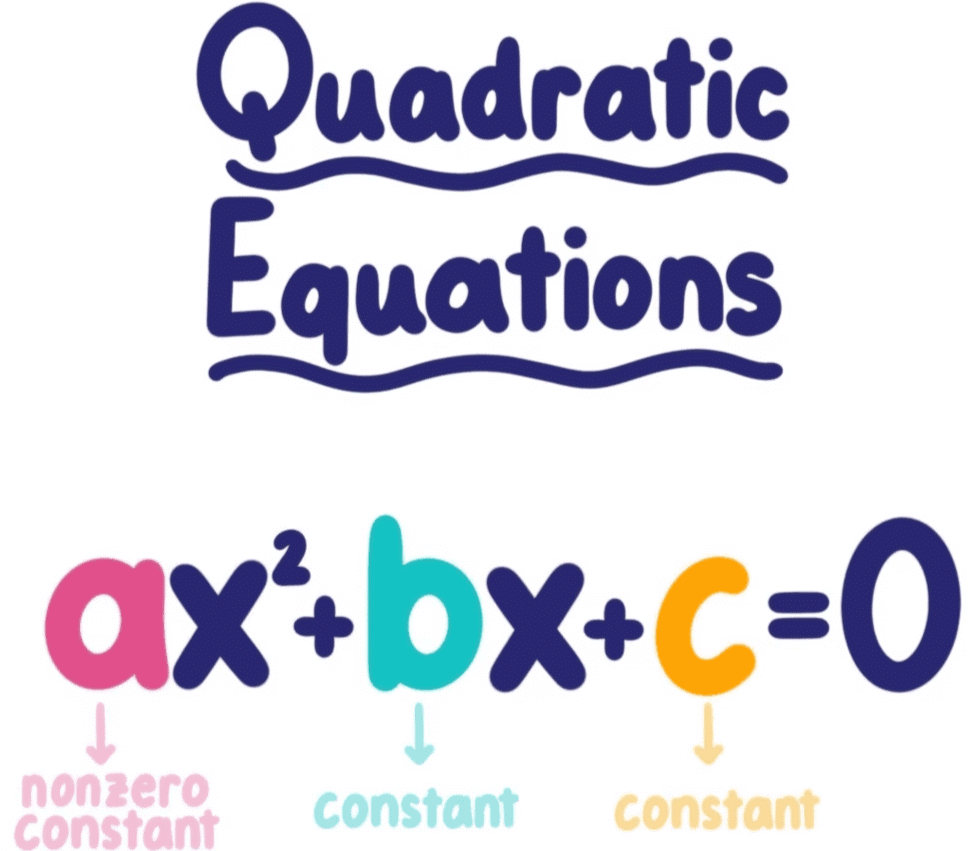
In bank exams, quadratic equations are often tested in both direct and word-problem formats. Here’s a guide to understanding and solving quadratic equations quickly, along with a shortcut to solve them in under a minute.
Theory
Standard Form of a Quadratic Equation:
The quadratic equation is generally written as:
ax² + bx + c = 0, where:
a is the coefficient of x²,
b is the coefficient of x,
c is the constant term.
Roots of the Quadratic Equation:
The roots of the quadratic equation can be calculated using:
Factorization Method
Quadratic Formula
Quadratic Formula:
The quadratic formula to find the roots of ax² + bx + c = 0 is:
x = [-b ± √(b² - 4ac)] / 2a
Where:
Δ = b² - 4ac is called the discriminant.
Important Formulas
Discriminant (Δ):
Δ = b² - 4ac
If Δ > 0, there are two distinct real roots.
If Δ = 0, there is exactly one real root (repeated root).
If Δ < 0, the roots are imaginary (complex).
Sum of Roots:
Sum of roots (r₁ + r₂) = -b / a
Product of Roots:
Product of roots (r₁ × r₂) = c / a
Tips for Solving Quadratic Equations Quickly in Bank Exams
1. Factorization for Simpler Equations:
Factorization is the quickest method if the equation can be easily factored. Look for pairs of numbers that multiply to c and add up to b.
Example: For x² + 5x + 6 = 0, you need two numbers whose product is 6 and sum is 5. The numbers are 2 and 3.
So, the equation becomes: (x + 2)(x + 3) = 0, and the roots are x = -2 and x = -3.
2. Use the Discriminant (Δ):
Always calculate the discriminant (Δ) before solving. If Δ < 0, you can immediately know that the equation has no real roots, saving you time in calculations.
3. Practice Regularly:
The key to solving these problems quickly is practice. Regularly solving practice problems will help you recognize factorization patterns and apply the quadratic formula more swiftly.
4. Simplify Square Roots Quickly:
Try to simplify square roots as much as possible. For example, √16 = 4, but √18 = √9 * √2 = 3√2.
Conclusion
Solving quadratic equations is a crucial skill for bank exams. By using the quadratic formula, factorization, and the discriminant method, you can solve most quadratic problems efficiently. For quick solutions, practice calculating Δ, simplifying square roots, and using factorization when possible. Remember, consistency in practice is the key to solving quadratic equations in under a minute.
FAQs on Cheatsheet: Quadratic Equation - Cheatsheets for Bank Exams
| 1. What is a quadratic equation? |  |
| 2. How can I quickly solve quadratic equations in bank exams? |  |
| 3. What are the important formulas related to quadratic equations? |  |
| 4. What tips can I follow to solve quadratic equations more efficiently? |  |
| 5. Why is understanding quadratic equations important for bank exams? |  |















