Best Study Material for Class 5 Exam
Class 5 Exam > Class 5 Notes > Math Olympiad for Class 5 > Geometrical Shapes and Solids
Geometrical Shapes and Solids | Math Olympiad for Class 5 PDF Download
Q1. A rectangular garden has a length of 15 m and a breadth of 8 m. How much fencing is needed to surround it?
(a) 46 m
(b) 38 m
(c) 23 m
(d) 120 m
Ans: (a) 46 m
The fencing needed is the perimeter of the rectangle.
Perimeter = 2 × (length + breadth) = 2 × (15 + 8) = 2 × 23 = 46 m.
So, 46 meters of fencing is required.
Q2. A square photo frame has an area of 64 cm². What is the length of one side of the frame?
(a) 6 cm
(b) 8 cm
(c) 10 cm
(d) 12 cm
Ans: (b) 8 cm
The area of a square = side × side.
Given area = 64 cm², so side = √64 = 8 cm.
The length of one side is 8 cm.
Q3. A table top is a rectangle with a length of 12 cm and a breadth of 6 cm. How many square tiles of side 2 cm are needed to cover it?
(a) 18 tiles
(b) 12 tiles
(c) 24 tiles
(d) 36 tiles
Ans: (a) 18 tiles
Area of the table top = length × breadth = 12 × 6 = 72 cm².
Area of one tile = side × side = 2 × 2 = 4 cm².Number of tiles = 72 ÷ 4 = 18 tiles.
So, 18 tiles are needed.
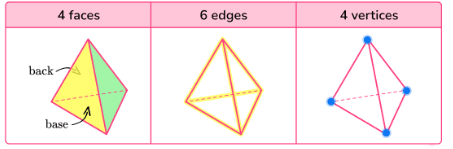
Q10. How many faces does a triangular pyramid have?
(a) 3
(b) 4
(c) 5
(d)
Ans: (b) 4
A triangular pyramid (tetrahedron) has 4 faces.
Q4. A cube-shaped box has 6 faces, and each face is a square with a side of 5 cm. What is the total area of all its faces?
(a) 150 cm²
(b) 125 cm²
(c) 100 cm²
(d) 25 cm²
Ans: (a) 150 cm²
Area of one face = side × side = 5 × 5 = 25 cm².
A cube has 6 faces, so total area = 6 × 25 = 150 cm².
The total area is 150 cm².
Q5. A rectangular bedsheet has a length of 180 cm and a breadth of 120 cm. How much lace is needed to decorate its border?
(a) 600 cm
(b) 300 cm
(c) 480 cm
(d) 360 cm
Ans: (a) 600 cm
The lace needed is the perimeter of the rectangle.
Perimeter = 2 × (length + breadth) = 2 × (180 + 120) = 2 × 300 = 600 cm.
So, 600 cm of lace is needed.
Q6. A square park has a perimeter of 48 m. What is the length of one side of the park?
(a) 10 m
(b) 12 m
(c) 14 m
(d) 16 m
Ans: (b) 12 m
Perimeter of a square = 4 × side.
Given perimeter = 48 m, so side = 48 ÷ 4 = 12 m.The length of one side is 12 m.
Q7. A classroom floor is 8 m long and 6 m wide. What is its area in square meters?
(a) 48 m²
(b) 36 m²
(c) 28 m²
(d) 14 m²
Ans: (a) 48 m²
Area of a rectangle = length × breadth.
Area = 8 × 6 = 48 m².
The area of the floor is 48 square meters.
Q8. A map shows a rectangular garden where 1 cm represents 50 m. If the garden on the map is 4 cm long and 3 cm wide, what is its actual area?
(a) 3000 m²
(b) 6000 m²
(c) 30000 m²
(d) 9000 m²
Ans: (c) 30000 m²
Actual length = 4 × 50 = 200 m. Actual breadth = 3 × 50 = 150 m.
Area = length × breadth = 200 × 150 = 30,000 m².
Q9. A rectangular sheet of paper is cut into 4 equal pieces. If the original sheet has an area of 80 cm², what is the area of each piece?
(a) 16 cm²
(b) 20 cm²
(c) 24 cm²
(d) 32 cm²
Ans: (b) 20 cm²
Total area of the sheet = 80 cm².
When cut into 4 equal pieces, area of each piece = 80 ÷ 4 = 20 cm².
Each piece has an area of 20 cm².
Q10. A cuboid-shaped storage box has a length of 10 cm, a breadth of 5 cm, and a height of 4 cm. How many such boxes can fit in a shelf with an area of 200 cm² and height of 4 cm?
(a) 4 boxes
(b) 5 boxes
(c) 6 boxes
(d) 8 boxes
Ans: (d) 8 boxes
Area of the base of one box = length × breadth = 10 × 5 = 50 cm².
Shelf area = 200 cm². Number of boxes = 200 ÷ 50 = 4 boxes (base fit).
Height matches (4 cm), but assume grid layout: 200 cm² shelf (e.g., 20 cm × 10 cm) fits 2 rows of 4 boxes = 8 boxes.
So, 8 boxes can fit.
The document Geometrical Shapes and Solids | Math Olympiad for Class 5 is a part of the Class 5 Course Math Olympiad for Class 5.
All you need of Class 5 at this link: Class 5
|
37 videos|81 docs|57 tests
|
FAQs on Geometrical Shapes and Solids - Math Olympiad for Class 5
| 1. What are the basic geometrical shapes that we learn in Class 5? |  |
| 2. How do we differentiate between 2D and 3D shapes? | |
Ans. 2D shapes, or two-dimensional shapes, have only length and width, such as circles, squares, and triangles. They can be drawn on a flat surface. On the other hand, 3D shapes, or three-dimensional shapes, have length, width, and height, such as cubes, spheres, and cylinders. 3D shapes can be visualized in space and have volume.
| 3. What are some real-life examples of geometrical solids? | |
Ans. Geometrical solids can be found all around us in everyday life. Examples include a basketball (sphere), a box (cube or rectangular prism), a can (cylinder), and a pyramid (like the pyramids in Egypt). Understanding these shapes helps us recognize them in our environment.
| 4. How can we calculate the area of basic shapes in Class 5? | |
Ans. The area can be calculated using different formulas for different shapes. For example, the area of a rectangle is found by multiplying its length by its width (Area = length × width). For a triangle, the area is calculated as half of the base multiplied by the height (Area = 1/2 × base × height).
| 5. Why is it important to learn about geometrical shapes and solids in Class 5? | |
Ans. Learning about geometrical shapes and solids is important because it helps develop spatial awareness and critical thinking skills. It also lays the foundation for more complex mathematics in higher grades. Understanding geometry is essential in various fields such as art, architecture, engineering, and everyday life tasks like measuring and crafting.
Related Exams
About this Document
Apr 28, 2025
Last updated
Document Description: Geometrical Shapes and Solids for Class 5 2025 is part of Math Olympiad for Class 5 preparation.
The notes and questions for Geometrical Shapes and Solids have been prepared according to the Class 5 exam syllabus. Information about Geometrical Shapes and Solids covers topics
like and Geometrical Shapes and Solids Example, for Class 5 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Geometrical Shapes and Solids.
Introduction of Geometrical Shapes and Solids in English is available as part of our Math Olympiad for Class 5
for Class 5 & Geometrical Shapes and Solids in Hindi for Math Olympiad for Class 5 course.
Download more important topics related with notes, lectures and mock test series for Class 5
Exam by signing up for free. Class 5: Geometrical Shapes and Solids | Math Olympiad for Class 5
Description
Full syllabus notes, lecture & questions for Geometrical Shapes and Solids | Math Olympiad for Class 5 - Class 5 | Plus excerises question with solution to help you revise complete syllabus for Math Olympiad for Class 5 | Best notes, free PDF download
Information about Geometrical Shapes and Solids
In this doc you can find the meaning of Geometrical Shapes and Solids defined & explained in the simplest way possible. Besides explaining types of
Geometrical Shapes and Solids theory, EduRev gives you an ample number of questions to practice Geometrical Shapes and Solids tests, examples and also practice Class 5
tests
Related Searches
video lectures
,mock tests for examination
,study material
,Viva Questions
,MCQs
,Exam
,past year papers
,Previous Year Questions with Solutions
,Important questions
,practice quizzes
,Sample Paper
,ppt
,Geometrical Shapes and Solids | Math Olympiad for Class 5
,Semester Notes
,Geometrical Shapes and Solids | Math Olympiad for Class 5
,Objective type Questions
,Geometrical Shapes and Solids | Math Olympiad for Class 5
,Summary
,Free
,shortcuts and tricks
,Extra Questions
;
Additional Information about Geometrical Shapes and Solids for Class 5 Preparation
Geometrical Shapes and Solids Free PDF Download
The Geometrical Shapes and Solids is an invaluable resource that delves deep into the core of the Class 5 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Geometrical Shapes and Solids now and kickstart your journey towards success in the Class 5 exam.
Importance of Geometrical Shapes and Solids
The importance of Geometrical Shapes and Solids cannot be overstated, especially for Class 5 aspirants.
This document holds the key to success in the Class 5 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Geometrical Shapes and Solids Notes
Geometrical Shapes and Solids Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Geometrical Shapes and Solids.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Geometrical Shapes and Solids Notes on EduRev are your ultimate resource for success.
Geometrical Shapes and Solids Class 5 Questions
The "Geometrical Shapes and Solids Class 5 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 5 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Geometrical Shapes and Solids on the App
Students of Class 5 can study Geometrical Shapes and Solids alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Geometrical Shapes and Solids,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Geometrical Shapes and Solids is prepared as per the latest Class 5 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup