सारांश: प्रतिशत | CSAT की तैयारी (हिंदी) - UPSC PDF Download

परिचय

• प्रतिशतों पर अध्याय विभिन्न प्रतिस्पर्धी परीक्षाओं में सबसे महत्वपूर्ण अध्यायों में से एक है (संख्यात्मक प्रणाली के अलावा)। ‘प्रतिशतों’ का महत्व इस तथ्य से स्पष्ट होता है कि व्यावसायिक अंकगणित के सभी अध्यायों (विशेषकर लाभ और हानि, अनुपात और समानुपात, समय और कार्य, और समय, गति और दूरी) में प्रतिशतों के उपयोग से संबंधित कई प्रश्न होते हैं।
• इसके अलावा, प्रतिशतों के अध्याय की समीक्षा करते समय आप जो गणना कौशल विकसित करते हैं, वह आपको डेटा इंटरप्रिटेशन (DI) गणनाओं को संभालने में मदद करेगा। इस विषय पर एक करीबी नज़र डालने से पता चलेगा कि किसी भी DI पेपर में कुल गणनाओं का कम से कम 80% जोड़ और प्रतिशतों पर आधारित होता है।

प्रतिशत क्या है?

‘प्रतिशत’ के नाम से स्पष्ट है कि ‘पर’ का अर्थ है हर और ‘सेंटी’ का अर्थ है सौ, अर्थात् “हर सौ के लिए”। यह डेटा और जानकारी की तुलना के लिए एक महत्वपूर्ण उपकरण है।

आना ने 40 में से 20 अंक प्राप्त किए। फिर, जब 100 के मुकाबले उसकी अंक संख्या का क्या होगा?

हल: एकात्मक विधि द्वारा हल करना: 40 अंकों में, आना ने 20 अंक प्राप्त किए। फिर, 100 अंकों में, आना को प्राप्त अंक = 20/40 × 100 = 50 अंक। इसका मतलब है कि जब इसे सौ के रूप में व्यक्त किया जाता है, तो यह प्रतिशत बन जाता है। इसका मतलब है कि आना ने 50% अंक प्राप्त किए।

प्रतिशत का सिद्धांत

• एक प्रतिशत केवल तब ही गणना की जा सकती है जब इसका एक आधार मूल्य या हर (denominator) हो। उपरोक्त उदाहरण में, आधार मूल्य या हर 40 था, जिसका मतलब है कि आना ने 40 में से 20 अंक प्राप्त किए (जो अंक प्राप्त करने की गणना का आधार मूल्य है)।
• प्रतिशत परिवर्तन का सिद्धांत = (अंतिम मूल्य - प्रारंभिक मूल्य) / प्रारंभिक मूल्य × 100

नोट: प्रारंभिक मूल्य को प्रतिशत परिवर्तन की गणना करते समय आधार या 'हर' के रूप में लिया जाता है।

प्रतिशत वृद्धि और घटावट

प्रतिशत का उपयोग अक्सर मात्रा में परिवर्तनों को इंगित करने के लिए किया जाता है। एक प्रतिशत एक अच्छी माप है जो दो अलग-अलग मात्राओं में परिवर्तन की तुलना करती है, जो कि प्रारंभिक (या आधार) मूल्य पर निर्भर करती है। उदाहरण के लिए:

• यदि कोई मात्रा a% बढ़ती है, तो उसका मान (100 + a)/100 से गुणा किया जाता है।
• यदि कोई मात्रा a% घटती है, तो उसका मान (100 - a)/100 से गुणा किया जाता है।

पूर्णांक मूल्य परिवर्तन बनाम प्रतिशत परिवर्तन

• पूर्णांक मूल्य परिवर्तन = मात्रा के माप में जो वास्तविक परिवर्तन होता है।
• प्रतिशत परिवर्तन = मूल मात्रा के माप के सापेक्ष पूर्णांक परिवर्तन।
• दो मात्राओं में एक ही पूर्णांक मूल्य परिवर्तन के लिए अलग-अलग प्रतिशत परिवर्तन हो सकते हैं, जो मूल मूल्य पर निर्भर करते हैं।

उदाहरण: यदि किसी शहर में औसत आर्द्रता 2018 में 32% से बढ़कर 2019 में 60% हो जाती है, तो आर्द्रता में वास्तविक परिवर्तन और प्रतिशत परिवर्तन क्या है?

हल: वास्तविक मान = अंतिम मान - मौलिक मान = 60 - 32 = 28 प्रतिशत परिवर्तन = (अंतिम मान - मौलिक मान)/ मौलिक मान = 28/32 * 100 = 87.5%

प्रतिशत बिंदु परिवर्तन बनाम प्रतिशत परिवर्तन

प्रतिशत बिंदु परिवर्तन बनाम प्रतिशत परिवर्तन

• प्रतिशत परिवर्तन और प्रतिशत बिंदु परिवर्तन के बीच के अंतर को समझना बहुत महत्वपूर्ण है।
• आइए हम निम्नलिखित उदाहरण द्वारा उनके बीच के अंतर को समझते हैं: आना ने अपनी अंतिम परीक्षा में 70 प्रतिशत अंक प्राप्त किए। अब, जब हम कहते हैं कि उसके अंक 5 प्रतिशत बढ़ गए हैं, इसका मतलब है कि पिछले प्राप्त अंकों की तुलना में 5% अंक बढ़े हैं, जो पिछले अंकों का 5% है, अर्थात् 5% of 70% = 3.5%।
• उसके नए प्राप्त अंक होंगे 70 + 3.5 = 73.5%। अब, जब हम कहते हैं कि उसके अंक 5 प्रतिशत बिंदुओं से बढ़ गए हैं, तो इसका अर्थ है कि उसके अंकों में 5% की निश्चित वृद्धि हुई है, पिछले अंकों की परवाह किए बिना, अर्थात् उसके नए प्राप्त अंक होंगे 70 + 5% = 75%।

इसलिए,

• प्रतिशत बिंदु परिवर्तन = दो प्रतिशत आंकड़ों का अंतर

प्रतिशतों का अनुप्रयोग

1. जनसंख्या:

यदि किसी नगर की मूल जनसंख्या P है और वार्षिक वृद्धि r% है, तो n वर्षों में जनसंख्या P' होगी:

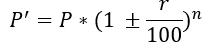
उदाहरण: बोइसर की जनसंख्या वर्तमान में 36000 लोग है। यदि जनसंख्या हर वर्ष 30% बढ़ती है, तो 3 वर्षों बाद जनसंख्या क्या होगी?

हल: जनसंख्या = 36000, r = 30% और n = 3 वर्ष। अतः आवश्यक जनसंख्या होगी:

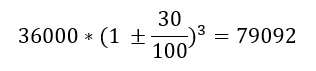
2. मूल्यह्रास:

किसी संपत्ति का मूल्य समय के साथ विभिन्न कारकों के कारण घटता है, जैसे कि पहनावा, पुरानी तकनीक, उपयोग आदि। इसे मूल्यह्रास कहा जाता है।

यदि P मूल मूल्य है और r प्रति वर्ष मूल्यह्रास की दर है, तो n वर्षों के बाद अंतिम मूल्य (F) निम्नलिखित होगा:

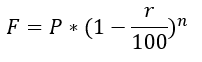
उदाहरण: 2019 में खरीदी गई एक iPhone हर वर्ष 10% मूल्यह्रासित हो गई है। यदि मौसम ने 2019 में iPhone के लिए ₹72,600 खर्च किए, तो 2022 में उसी दिन इसका मूल्य क्या होगा?

हल: P = 72,600, r = 10%, n = 3 वर्ष। F = 52,295.4

महत्वपूर्ण सूत्र

• संख्याओं का प्रतिशत ज्ञात करना: सूत्र: प्रतिशत = (मूल्य × प्रतिशत) / 100
  उदाहरण: 200 का 25% ज्ञात करें। प्रतिशत = (200 × 25) / 100 = 50
• प्रतिशत से मूल्य ज्ञात करना: सूत्र: मूल्य = (प्रतिशत × कुल) / 100
  उदाहरण: 500 का 30% क्या है? मूल्य = (30 × 500) / 100 = 150
• प्रतिशत वृद्धि या कमी: सूत्र: प्रतिशत परिवर्तन = [(नया मूल्य - पुराना मूल्य) / पुराना मूल्य] × 100
  उदाहरण: यदि किसी पुस्तक की कीमत 200 से 250 हो जाती है, तो प्रतिशत वृद्धि होगी: प्रतिशत परिवर्तन = [(250 - 200) / 200] × 100 = 25%
• प्रतिशत से कुल मूल्य ज्ञात करना: सूत्र: कुल = (मूल्य × 100) / प्रतिशत
  उदाहरण: यदि एक संख्या का 20% 50 है, तो कुल ज्ञात करें। कुल = (50 × 100) / 20 = 250
• भिन्न को प्रतिशत में परिवर्तित करना: सूत्र: प्रतिशत = (भिन्न × 100)%
  उदाहरण: 3/4 को प्रतिशत में परिवर्तित करें। प्रतिशत = (3/4) × 100 = 75%
• प्रतिशत लाभ या हानि ज्ञात करना: सूत्र: लाभ या हानि प्रतिशत = [(लाभ या हानि) / लागत मूल्य] × 100
  उदाहरण: यदि किसी वस्तु को 100 में खरीदा गया है और 120 में बेचा गया है, तो लाभ प्रतिशत = [(120 - 100) / 100] × 100 = 20%

हल किए गए उदाहरण

उदाहरण 1: एक रिपोर्ट में 20 पृष्ठ हैं, प्रत्येक में 55 पंक्तियाँ हैं, और प्रत्येक पंक्ति में 65 वर्ण हैं। इस रिपोर्ट को ऐसे पृष्ठों पर कम किया गया है जिनमें प्रत्येक में 65 पंक्तियाँ हैं, और प्रत्येक पंक्ति में 70 वर्ण हैं। पृष्ठों की संख्या में प्रतिशत कमी के निकटतम:

मान लीजिए कि x वह पृष्ठ है जो रिपोर्ट को फिर से टाइप करने पर आवश्यक है। अब, हम कार्य समकक्षता विधि का उपयोग कर सकते हैं:

20 × 55 × 65 = 70 × 65 × x

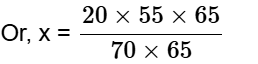
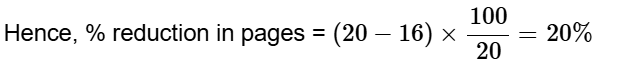
उदाहरण 2: मतदाताओं का 2/5 हिस्सा A के लिए मतदान करने का वादा करता है, और बाकी B के लिए मतदान करने का वादा करते हैं। इनमें से, अंतिम दिन, 15% मतदाता A के लिए मतदान करने के अपने वादे से मुकर गए, और 25% मतदाता B के लिए मतदान करने के अपने वादे से मुकर गए, और A 200 मतों से हार गया। तब कुल मतदाताओं की संख्या है:

मान लीजिए कि कुल मतदाता 500 हैं। A के लिए मतदान करने का वादा करने वाले मतदाता: ⇒ 2/5 × 500 ⇒ 200। शेष ने B के लिए मतदान करने का वादा किया: ⇒ 300 ने B के लिए मतदान करने का वादा किया। 15% A के लिए मतदान करने से मुकर गए: ⇒ 15/100 × 200 ⇒ 30 मतदाता जो A के लिए मतदान करने का वादा किया था, B के लिए मतदान किया। 25% B के लिए मतदान करने से मुकर गए: ⇒ 25/100 × 300 ⇒ 75 मतदाता जो B के लिए मतदान करने का वादा किया था, A के लिए मतदान किया। B के अंतिम वोट: ⇒ 300 – 75 = 225। A के अंतिम वोट: ⇒ 200 – 30 = 170। A 255 – 245 = 10 मतों से हार गया। प्रश्न के अनुसार: ⇒ 10 = 200 ⇒ 1 = 200/10 = 20। कुल मतदाता संख्या = 500 × 20 = 10,000

∴ कुल मतदाता संख्या 10,000 है।

उदाहरण 3: एक व्यक्ति जिसके पास एक निश्चित राशि है, बाजार जाता है। वह 50 संतरे या 40 आम खरीद सकता है। वह टैक्सी भाड़े के लिए 10% राशि रखता है और 20 आम खरीदता है, और शेष राशि से वह संतरे खरीदता है। वह कितने संतरे खरीद सकता है:

व्यक्ति 50 संतरे या 40 आम खरीद सकता है। एक संतरे की कीमत Rs. x मान लें। व्यक्ति के पास कुल राशि = Rs. 50x है। 40 आमों की लागत 50x है, इसलिए एक आम की लागत 1.25x है। कुल राशि का 10% टैक्सी भाड़े के लिए रखा जाता है = 10% of 50x = 5x। 20 आम खरीदे जाते हैं, जिसकी लागत 20 * 1.25x = 25x है। व्यक्ति के पास बचे हुए पैसे = 50x – (टैक्सी भाड़ा) – (आमों की लागत) = 50x – 5x – 25x = 20x। एक संतरे की कीमत Rs. x है, इसलिए Rs. 20x के साथ 20 संतरे खरीदे जा सकते हैं। इस प्रकार, व्यक्ति ने 20 संतरे खरीदे।

उदाहरण 4: एक निश्चित कंपनी के 40% कर्मचारी पुरुष हैं, और 75% पुरुषों की आय Rs. 25,000 प्रति वर्ष से अधिक है। यदि कंपनी के 45% कर्मचारी Rs. 25,000 प्रति वर्ष से अधिक कमाते हैं, तो कंपनी में काम करने वाली महिलाओं में से कितने प्रतिशत ने Rs. 25,000 या उससे कम कमाया?

कंपनी में कुल कर्मचारियों की संख्या x मान लें। तब पुरुषों और महिलाओं की संख्या क्रमशः 0.4x और 0.6x है। 75% पुरुष Rs. 25,000 से अधिक कमाते हैं ⇒ 0.75 x 0.4 x = 0.3 x। Rs. 25,000 से अधिक कमाने वाले कुल कर्मचारियों की संख्या = 45% x = 0.45 x। Rs. 25,000 से अधिक कमाने वाली महिलाओं की संख्या = कुल कर्मचारी जो Rs. 25,000 से अधिक कमाते हैं - Rs. 25,000 से अधिक कमाने वाले पुरुषों की संख्या = 0.45 x – 0.30 x = 0.15 x। Rs. 25,000 या उससे कम कमाने वाली महिलाओं की संख्या = 0.60 x – 0.15 x = 0.45 x। कंपनी में काम करने वाली महिलाओं में से जो Rs. 25,000 या उससे कम कमाते हैं, उनका भाग = (0.45x/0.60x) = 45/60 = 3/4।

उदाहरण 5: 60 छात्रों की एक कक्षा में, 20% छात्र पुरुष हैं। 75% महिला छात्रों ने पूरे वर्ग के लिए आयोजित परीक्षा में उत्तीर्ण किया। परीक्षा में उत्तीर्ण हुई महिला छात्रों की संख्या क्या है?

समाधान: चूंकि यह दिया गया है कि छात्रों में से 20% पुरुष हैं, इसका मतलब है कि शेष 80% महिलाएँ हैं।

• महिलाओं की संख्या: (80/100) x 60 = 48
• उत्तीर्ण महिला छात्रों की संख्या: 48 का 75% = 36