हल किए गए उदाहरण: प्रतिशत | CSAT की तैयारी (हिंदी) - UPSC PDF Download

प्रतिशत का अर्थ क्या है?

• शब्द 'प्रतिशत' का अर्थ है "हर सौ के लिए"।
• एक भिन्न, जिसका हर (denominator) 100 है, उसे प्रतिशत कहते हैं और भिन्न का अंश (numerator) दर प्रतिशत कहलाता है।
• इसलिए, जब हम कहते हैं कि एक व्यक्ति ने 20 प्रतिशत लाभ कमाया, तो इसका अर्थ है कि उसने प्रत्येक सौ रुपये में 20 रुपये कमाए, जिसे हम 20/100 रुपये प्रति रुपये के रूप में व्यक्त कर सकते हैं।

प्रतिशत का संक्षिप्त रूप p.c. है और इसे सामान्यतः % द्वारा दर्शाया जाता है।

उदाहरण 1: 84% किसी विशेष कुल का 630 अंक है। 90% कितना होगा? (क) 750 (ख) 675 (ग) 450 (घ) 550 (घ) इनमें से कोई नहीं

उत्तर: (ख) समाधान। आवश्यक उत्तर है:

उदाहरण 2: दो संख्याएँ तीसरी संख्या से क्रमशः 25% और 20% अधिक हैं। पहले संख्या का प्रतिशत दूसरे संख्या के बराबर क्या है? (क) 92% (ख) 94% (ग) 96% (घ) 98% (घ) इनमें से कोई नहीं

उत्तर: (ग) समाधान। मान लें कि तीसरी संख्या 100 है। तो पहली संख्या 125 और दूसरी संख्या 120 है। तो आवश्यक उत्तर है:

बुनियादी बातें

प्रतिशत और भिन्न के समकक्ष

• यदि कोई आपसे 50% को भिन्न में व्यक्त करने के लिए कहता है, तो आप क्या करेंगे? निश्चित रूप से, आप इसका उत्तर देंगे।
• यह मूल्य वास्तव में क्या दर्शाता है? यह कुछ और नहीं बल्कि दिए गए प्रतिशत का भिन्नात्मक समकक्ष है।

उदाहरण 3: A, B से 20% अधिक कमा रहा है, जो C से 20% कम कमाता है। A, C से कितना अधिक या कम कमा रहा है?

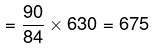
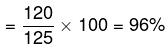
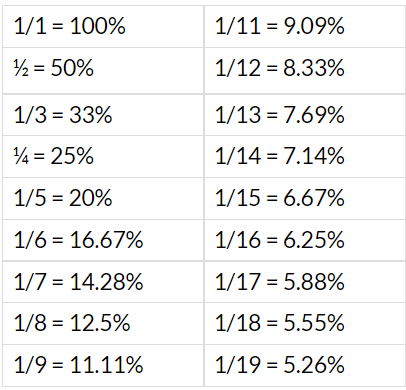
समाधान।

(1) और (2) से, हमारे पास है

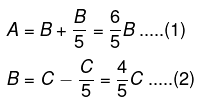
अर्थात, A, C से 4% कम है।

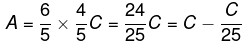
या मान लें कि ‘C’ 100 कमाता है। इस प्रकार, B 80 कमाता है और A 96 कमाता है। इसलिए ‘A’ C से 4% कम कमाता है।

गुणन कारक

• प्रतिशत वृद्धि या कमी के साथ काम करते समय, अपने मन में निम्नलिखित स्केल की कल्पना करें, जिसमें 100% (= 1) केंद्र में है।
• इसलिए हम कह सकते हैं कि 10% वृद्धि का गुणन कारक (M.F) 1.1 है और 15% कमी का 0.85 है।
• x% की वृद्धि का मतलब है कि मूल्य 100% के दाहिनी ओर है और इसके विपरीत।
• मान लें कि संख्या X है। X में 10% की वृद्धि होगी: X + 0.1X = 1.1X
• X में 1% की वृद्धि होगी: X + 0.01X = 1.01X
• X में 0.1% की वृद्धि होगी: X + 0.001X = 1.001X
• X में 10% की कमी होगी: X - 0.1X = 0.9X
• X में 1% की कमी होगी: X - 0.01X = 0.99X
• X में 0.1% की कमी होगी: X - 0.001X = 0.999X
• X में 200% की वृद्धि होगी: X + 2X = 3X
• X में 300% की कमी होगी: X - 3X = -2X

उदाहरण 4: नारियल का तेल अब 27 रुपये प्रति किलो बेचा जा रहा है। पिछले महीने इसकी लागत 24 रुपये प्रति किलो थी। पता लगाएं कि एक परिवार को अपने खर्च को समान रखने के लिए अपनी खपत को कितने प्रतिशत कम करना चाहिए।

समाधान। मान लें कि पिछले वर्ष की खपत 1 किलोग्राम है, तब इसकी लागत ₹24 थी। लेकिन अब ₹24 में केवल 24/27 किलोग्राम तेल मिलेगा। तो खपत में % कमी कितनी होगी।

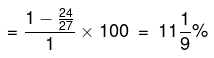
सफलता प्रतिशत परिवर्तन

• एक वर्ष में किसी शहर की जनसंख्या 10% बढ़ती है और अगले वर्ष फिर से 10% बढ़ती है, तो दो वर्षों में जनसंख्या में कुल वृद्धि क्या होगी। सामान्य उत्तर 20% है जो गलत है। क्यों? चलिए देखते हैं यदि मूल जनसंख्या = P है।

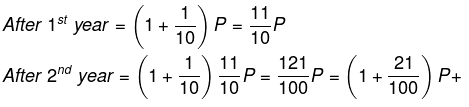
• अर्थात, मूल मान का 21% बढ़ता है। इस क्रमिक परिवर्तन को नीचे बताए गए शॉर्टकट तरीके से गणना की जा सकती है:
• चलो दो मात्राओं के उत्पाद A = a x b पर विचार करते हैं। यदि a और b एक निश्चित प्रतिशत जैसे x और y के अनुसार बदलते हैं (बढ़ते या घटते हैं), तो उनके उत्पाद में कुल प्रतिशत परिवर्तन निम्नलिखित सूत्र द्वारा दिया गया है:

उदाहरण 5। यदि दूध और पानी के मिश्रण की मात्रा को पानी डालकर 25% बढ़ा दिया जाता है। तो दूध की सांद्रता में कितने प्रतिशत की कमी आती है?

समाधान: प्रारंभ में, 100 लिटर का घोल है, जिसमें से x लिटर दूध है। इसलिए दूध की संवेदनशीलता x/100 है। अब यह x/125 है। इसलिए प्रतिशत कमी

यह सूत्र तब भी सही है जब लगातार परिवर्तन होते हैं, जैसे जनसंख्या में वृद्धि या कमी के मामले में। लेकिन जब लगातार 2 से अधिक परिवर्तन होते हैं या 2 से अधिक मात्राओं का गुणन होता है, जैसे कि मात्रा के मामले में, तब सावधानी बरतनी चाहिए।

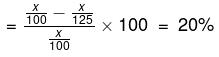
• इन मामलों में हमें वही सूत्र दो बार लागू करना होगा।
• यदि x% और y% की लगातार वृद्धि होती है, तो शुद्ध परिवर्तन होगा।
• यदि x% और y% की लगातार छूट होती है, तो कुल छूट होगी।
• यदि x% वृद्धि होती है और फिर x% कमी होती है, तो शुद्ध परिवर्तन होगा।
• यदि मान भिन्न हैं, तो शुद्ध परिवर्तन

उदाहरण 6: यदि A को 20% बढ़ाया जाए और B को 20% घटाया जाए, तो दोनों मात्राएँ समान होंगी। B का A के मुकाबले प्रतिशत क्या है।

समाधान: यदि A को 20% बढ़ाया जाता है, तो यह 1.2 A बन जाएगा। और यदि B को 20% घटाया जाता है, तो यह 0.8 B बन जाएगा। यह दिया गया है कि 1.2 A = 0.8 B,

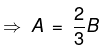
A = 0.66 B ∴ A, B का 66.66% है।

उदाहरण 7: यदि A, B का 3 गुना है, तो B, A का कितना प्रतिशत है।

समाधान: A = 3B। ⇒ B = A/3 = 0.33 A ∴ B, A का 33% है।

उदाहरण 8: यदि 'x' को 20% और 25% लगातार बढ़ाया जाता है, तो इसका मान 30 से बढ़ जाता है। X का मान क्या है?

समाधान: यदि X को 20% बढ़ाया जाता है, तो यह बन जाएगा

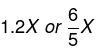
यदि इसे फिर से 25% बढ़ाया जाता है, तो इसका मान बन जाता है

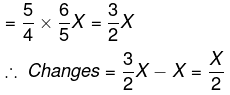
यह दिया गया है 30। (या) यदि एक मान लगातार X% और Y% बढ़ता है, तो इसका मान बदलता है

इसलिए X में वृद्धि होती है

∴ X का 50% 30 के बराबर है। ∴ X = 60।

उदाहरण 9। एक व्यक्ति अपने वेतन का 30% भोजन पर खर्च करता है और शेष राशि का 20% किराए पर और शेष का 20% अन्य खर्चों पर। यदि वह ₹8960 बचाता है, तो उसका वेतन क्या है?

हल। मान लीजिए कि उसका वेतन 'K' है। यदि उसने भोजन पर 30% खर्च किया, तो उसके पास K का 70% बच जाएगा, यानी 0.7K। इस पर उसने किराए पर 20% खर्च किया और 80% बचता है।

इस पर अन्य खर्चों पर 20% खर्च करने के बाद उसके पास 80% बचता है। यानी यह ₹8960 के बराबर है। ⇒ K = 20000।

उदाहरण 10। पिछले वर्ष एक कर्मचारी अपने वेतन का 40% बचाता था। लेकिन अब उसका वेतन 50% बढ़ गया है और खर्च भी 20% बढ़ गए हैं। अब उसकी बचत का प्रतिशत क्या है?

हल। मान लीजिए कि 'X' पिछले वर्ष कर्मचारी का वेतन था। चूंकि उसकी बचत 40% थी, उसके खर्च 60% यानी 0.6X थे। वर्तमान में, उसका वेतन 1.5X है और खर्च 1.2 (0.6X) = 0.72X हैं। ∴ बचत = 1.5X - 0.72X = 0.78X।

आइए कुछ उदाहरण देखें और प्रतिशत के बारे में और जानें

उदाहरण 1। 60 छात्रों की कक्षा में, 20% पुरुष हैं। कक्षा के लिए आयोजित परीक्षा में 75% महिला छात्रों ने परीक्षा उत्तीर्ण की। परीक्षा उत्तीर्ण करने वाली महिला छात्रों की संख्या क्या है?

हल। चूंकि यह दिया गया है कि 20% छात्र पुरुष हैं, इसका मतलब है कि शेष 80% महिला हैं। महिलाओं की संख्या - (80/100)*60 = 48। परीक्षा उत्तीर्ण करने वाली महिला छात्रों की संख्या = 48 का 75% = 36।

उदाहरण 2। - 33.33% का अनुमानित मूल्य खोजें 99 का और 81.81% का 495 का।

हल। 33.33% = 1/3 और 81.81% = 9/11। अब समस्या आसान हो जाती है - 99/3 और 495*9/11 = 438।

निम्नलिखित गणनाएँ ध्यान में रखी जानी चाहिए:

• 1/1 = 100%
• ½ = 50%
• 1/3 = 33.33%
• ¼ = 25%
• 1/5 = 20%
• 1/6 = 16.66%
• 1/7 = 14.28%
• 1/8 = 12.5%
• 1/9 = 11.11%
• 1/10 = 10%
• 1/11 = 9.09%
• 1/12 = 8.33%
• और इसी तरह।

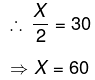
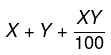
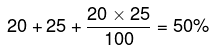
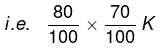
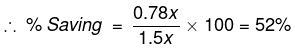
यह कुछ गणनाओं के दौरान सहायक हो सकता है। उदाहरण के लिए: 63.63% = (9.09*7)% = 7/11। इसी तरह, 44.44% = 4/9 और 37.5% = 3/8। प्रतिशत वृद्धि या कमी से संबंधित समस्याएं एक महत्वपूर्ण भाग बनाती हैं।

उदाहरण 3: गेहूं का उत्पादन 50 मिलियन टन से बढ़कर 70 मिलियन टन हो गया। प्रतिशत वृद्धि क्या है?

हल: प्रतिशत वृद्धि = (वास्तविक वृद्धि / मूल मात्रा) * 100
प्रतिशत कमी = (वास्तविक कमी / मूल मात्रा) * 100
इसलिए, प्रतिशत वृद्धि = (20/50)*100 = 40%

उदाहरण 4: गेहूं का उत्पादन 50 मिलियन टन के मूल्य पर 40% बढ़ा। वर्तमान गेहूं का उत्पादन क्या है?

हल: जब भी किसी मात्रा पर कोई प्रतिशत वृद्धि या कमी होती है, तो हम वास्तविक वृद्धि/कमी की गणना करने के बजाय मात्रा का नया मान सीधे गणना कर सकते हैं और फिर मूल मात्रा से जोड़/घटा सकते हैं। ऊपर के प्रश्न में, हम कह सकते हैं कि अंतिम मात्रा को 50 मिलियन * 1.4 = 70 मिलियन के रूप में गणना किया जा सकता है।

(जहां 1.4 = 1 + 0.4, 0.4 40% का दशमलव समकक्ष है)

सामान्यीकृत करते हुए, हम कह सकते हैं कि यदि प्रतिशत वृद्धि p% है, तो नया मान (p/100 + 1) गुना पुराने मान के बराबर है। इसके विपरीत, यदि नया मान k गुना पुराने मान के बराबर है, तो प्रतिशत वृद्धि (k-1)*100 है।

उदाहरण 5: यदि A की तनख्वाह B की तनख्वाह से 20% अधिक है, तो B की तनख्वाह A की तनख्वाह से कितनी प्रतिशत कम है?

हल: मान लीजिए B की तनख्वाह 100 है। इसलिए, A की तनख्वाह = 1.2 * 100 = 120। B की तनख्वाह A से 20 कम है। प्रतिशत में अंतर = (20/120)*100 = 16.66% (ध्यान दें कि हर बार A की तनख्वाह संदर्भ बिंदु के रूप में ली गई है, इसलिए हर बार हर गणना में 120 भागफल है।)

उदाहरण 6। किसी वस्तु की कीमत 30% बढ़ गई। इसे वास्तविक स्तर पर लाने के लिए इसे कितने प्रतिशत कम किया जाना चाहिए?

समाधान। प्रारंभिक कीमत = 100 (या x) नई कीमत = 1.3 * 100 = 130 (या 1.3x) अंतर = 30 (या 0.3x) कीमत को 30% कम करने की आवश्यकता है, लेकिन संदर्भ बिंदु 130 से = (30/130) * 100 = 23.07% (या (0.3x/1.3x) * 100)

उदाहरण 7। यदि मेरी वेतन 30% बढ़ी और फिर 30% घट गई, तो कुल परिवर्तन क्या है?

समाधान। मान लीजिए मेरी वेतन x है। वृद्धि के बाद - 1.3x। कमी के बाद - (0.7) * 1.3x = 0.91x, जो हमें मूल वेतन x से 9% की कमी देता है।

• सामान्यीकरण करें, यदि कोई मात्रा p% बढ़ती है और फिर p% घटती है, तो कुल कमी (p²)/100 % होती है। हमने सभी बुनियादी उदाहरणों और अवधारणाओं पर विचार किया है। चलिए कुछ समस्याओं को हल करते हैं।

समस्या 1। यदि चीनी की कीमत 10% बढ़ती है, तो कुल खर्च को समान बनाए रखने के लिए उपभोग की गई मात्रा में कितना प्रतिशत कमी होनी चाहिए?

समाधान। मान लीजिए s चीनी की कीमत है और q उपभोग की गई मात्रा है। चूंकि कीमत 10% बढ़ी है, नई कीमत 1.1s है। मान लीजिए उपभोग की मात्रा r है। चूंकि कुल खर्च समान रहना है, हमें मिलता है: s * q = 1.1s * r, इसलिए, r = q/1.1। उपभोग में प्रतिशत कमी है: (q - q/1.1) * 100 / q = 100/11 %।

समस्या 2।

एक कला दुकान के मालिक अपने व्यवसाय को निम्नलिखित तरीके से संचालित करते हैं। हर कुछ समय बाद वह अपनी कीमतें X% बढ़ाते हैं, फिर कुछ समय बाद वह सभी नई कीमतों को X% कम करते हैं। एक ऐसे ऊपर-नीचे चक्र के बाद, एक पेंटिंग की कीमत Rs.441 कम हो गई। दूसरे ऊपर-नीचे चक्र के बाद, पेंटिंग Rs.1944.811 में बेची गई। पेंटिंग की मूल कीमत (Rs में) क्या थी?

समस्या समाधान।

समस्या 3। एक समाज ने एक नए भवन के लिए आवश्यक राशि का 60% जुटा लिया है, जिसमें उसने पहले से अनुरोध किए गए लोगों से औसतन ₹300 का योगदान प्राप्त किया है। पहले से अनुरोध किए गए लोग उन लोगों का 80% हैं, जिनसे समाज योगदान मांगने की योजना बना रहा है। समाज चाहता है कि वह नए भवन के लिए आवश्यक राशि पूरी तरह से जुटा ले। शेष लोगों से औसत योगदान क्या होना चाहिए, जिनसे अभी अनुरोध किया जाना है?

समाधान। मान लें कि समाज को नए भवन के लिए आवश्यकता राशि A है। पहले से अनुरोध किए गए और जिनसे अनुरोध किया जाना है, उनकी कुल संख्या को N मान लें।

• 60A/100 = 300 (80N/100) – (1)
• यदि औसत योगदान जो समाज को शेष लोगों से प्राप्त करना चाहिए, उसे x मानते हैं।
• 40A/100 = x(20N/100) – (2)

समीकरण 2 को 1 से विभाजित करते हैं: x = 800