More Fractions | Year 3 Mathematics IGCSE (Cambridge) - Class 3 PDF Download
| Table of contents |

|
| Introduction: |

|
| 1. What are Fractions? |

|
| 2. Fractions of Shapes |

|
| 3. Visualizing Fractions |

|
| 4. Identifying Fractions in Real-Life Objects |

|
| 5. Working with Fractions |

|
| 6. Practice Questions: |

|
Introduction:
In this chapter, we will explore the concept of fractions, particularly fractions of shapes. Fractions help us understand parts of a whole. By the end of this chapter, you will be able to recognize fractions in different shapes, understand how to divide shapes into parts, and identify fractions in real-life situations.
1. What are Fractions?
- Definition of Fractions:
A fraction represents a part of a whole. It is written as a numerator (top number) and a denominator (bottom number). The numerator tells us how many parts we have, and the denominator tells us how many parts the whole is divided into.
- Numerator and Denominator:
In the fraction 3/4:
- 3 is the numerator, representing the number of parts we have.
- 4 is the denominator, representing the total number of parts the whole is divided into.
- Examples of Fractions:
Fractions can be represented as parts of different shapes. For example, if we divide a square into 4 equal parts and shade 3 of them, we have the fraction 3/4.
2. Fractions of Shapes
- Dividing Shapes into Equal Parts:
To understand fractions, we need to divide shapes into equal parts. These parts represent fractions of the whole shape. A shape can be divided into halves, thirds, quarters, and so on. Each part is a fraction of the entire shape.
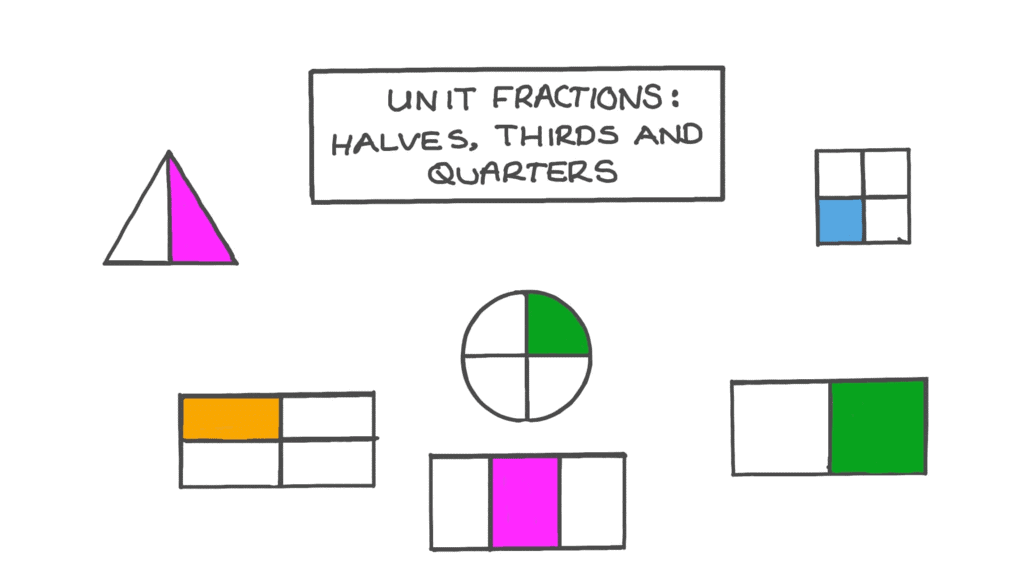
- Examples of Fractions in Shapes:
Let's consider some examples of dividing shapes into equal parts:
- Halves: A shape divided into 2 equal parts. Each part is 1/2.
- Thirds: A shape divided into 3 equal parts. Each part is 1/3.
- Quarters: A shape divided into 4 equal parts. Each part is 1/4.
3. Visualizing Fractions
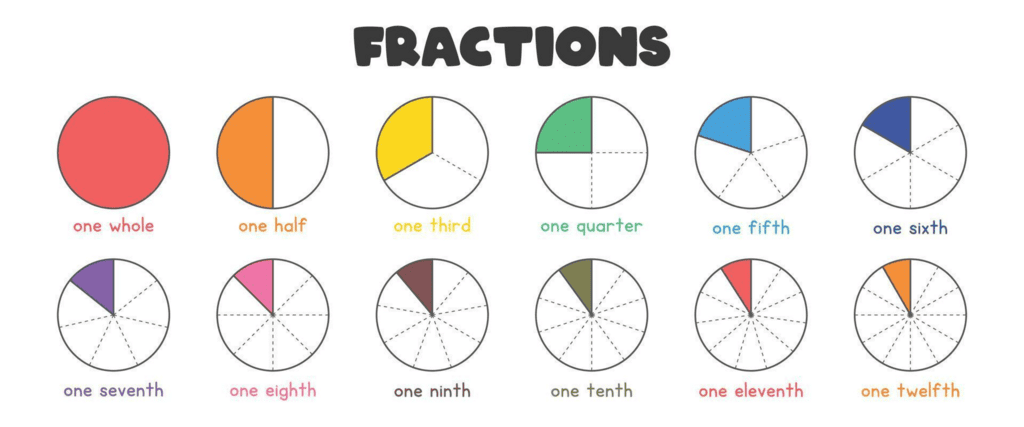
Consider a circle divided into 4 equal parts (quarters). If we shade 1 part of the circle, we have shaded 1/4 of the circle.
- Fraction of a Rectangle:
Similarly, a rectangle can be divided into equal parts. For example, a rectangle divided into 3 equal parts gives us 1/3 of the rectangle for each part.
- Fraction of a Square:
A square can be divided into halves, thirds, or quarters, and we can represent these fractions visually by shading or counting the parts.
4. Identifying Fractions in Real-Life Objects
- Using Food to Understand Fractions:
Food items like pizzas and cakes are great examples to explain fractions. If a pizza is cut into 8 equal slices, and you eat 3 slices, you’ve eaten
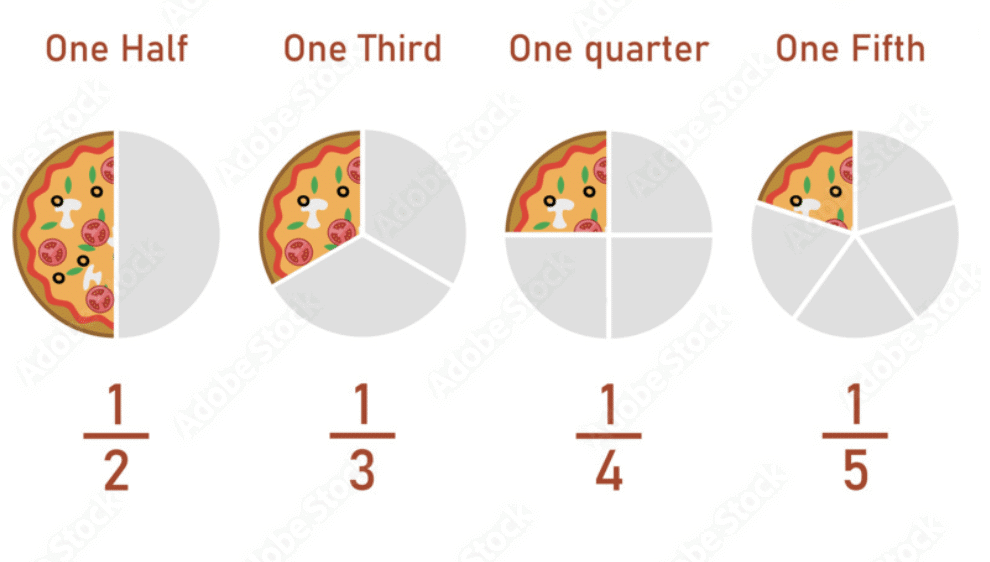
- Real-Life Examples of Fractions:
Other examples include:
- A chocolate bar broken into equal parts. If you eat half of the bar, you’ve eaten 1/2 of it.
- A group of 5 friends where 2 are wearing hats. The fraction of friends with hats is 2/5.
5. Working with Fractions
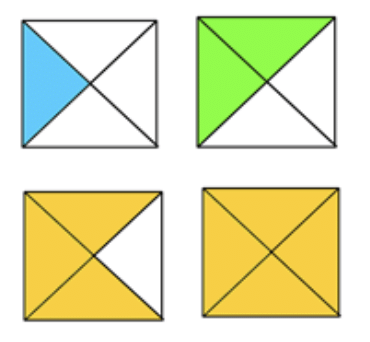
- Shading Parts of a Shape:
One way to show fractions is by shading parts of a shape. For example, if we shade 3 out of 4 equal parts of a square, we show 3/4 of the square.
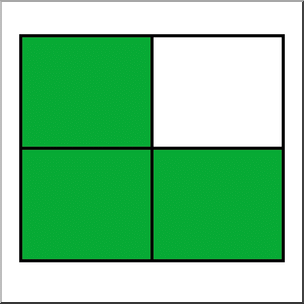
- Matching Fractions to Shapes:
We can match fractions to shapes by dividing them into equal parts and shading the appropriate number of parts. For example, a shape divided into 5 parts and 2 parts shaded represents 2/5.
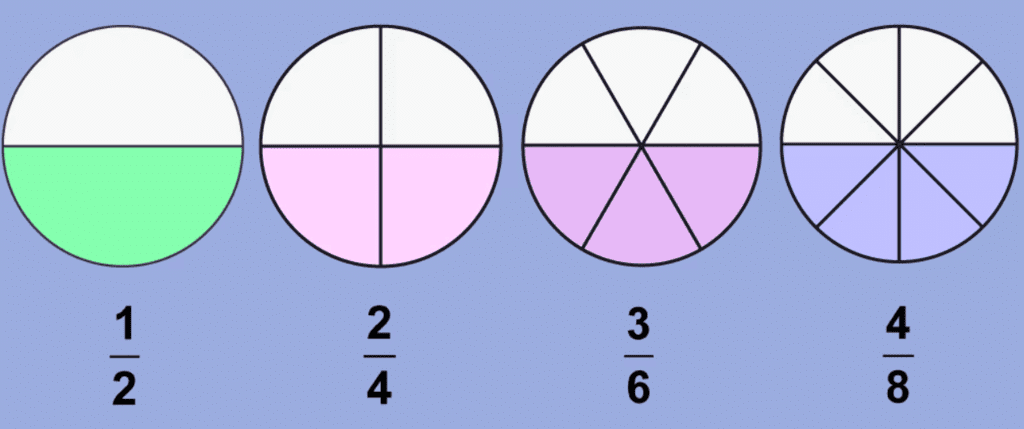
- Fraction Equivalence:
Some fractions can represent the same amount. For example, 2/4 is the same as 1/2. This is called fraction equivalence.
6. Practice Questions:
- Shade 1/2 of the following shapes.
- What fraction of the circle is shaded if 3 out of 6 parts are shaded?
- Divide the square into 4 equal parts and shade 3 of them. What fraction of the square is shaded?
- If you have a pizza with 8 slices and you eat 4 slices, what fraction of the pizza did you eat?
- Draw a rectangle divided into 3 parts. Shade 1 part. What fraction is shaded?
|
65 docs|19 tests
|
FAQs on More Fractions - Year 3 Mathematics IGCSE (Cambridge) - Class 3
| 1. What are the basic parts of a fraction? |  |
| 2. How can I visualize fractions using shapes? |  |
| 3. Where can I find fractions in real-life objects? |  |
| 4. What are some common ways to work with fractions? |  |
| 5. What practice questions can help me understand fractions better? |  |



















