NCERT Solutions for Class 4 Maths Chapter 11 - Fun with Symmetry
| Table of contents |

|
| Page No. 164 |

|
| Page no. 167 |

|
| Page 168 |

|
| Page 169 |

|
| Page 170 |

|
| Page 171 |

|
| Page No. 172 |

|
Page No. 164
Let Us Do
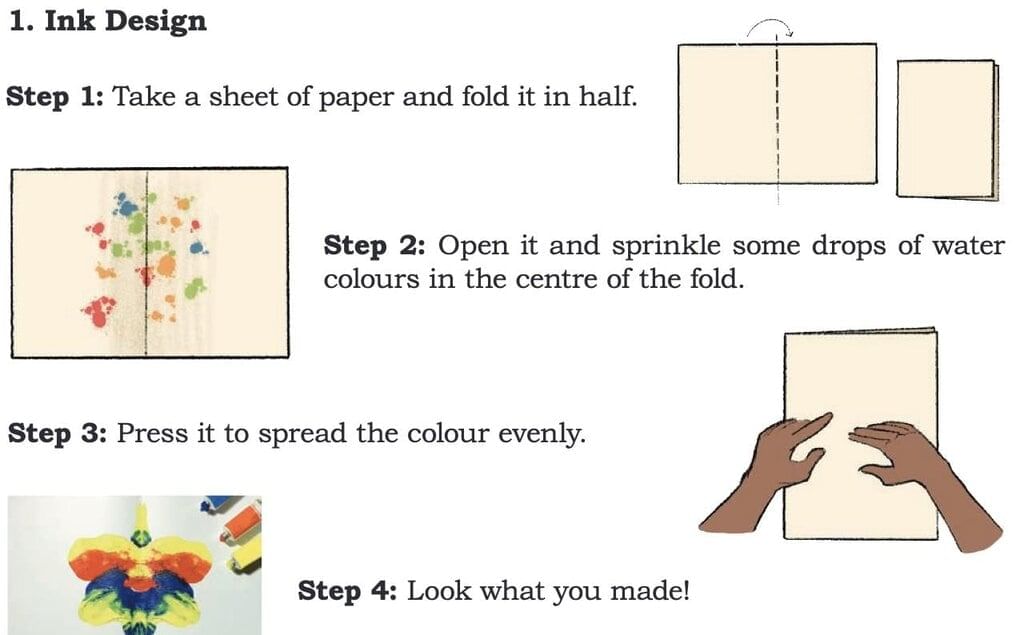
Is it a symmetrical pattern?
Where would you draw the line that divides this design into two equal halves? Isn't this line called the line of symmetry?
Ans: Yes, folding paper and pressing spreads ink evenly, creates mirror images. Yes, there is a line of symmetry along the fold (vertical center).
2. Making a paper airplane
Follow the steps.
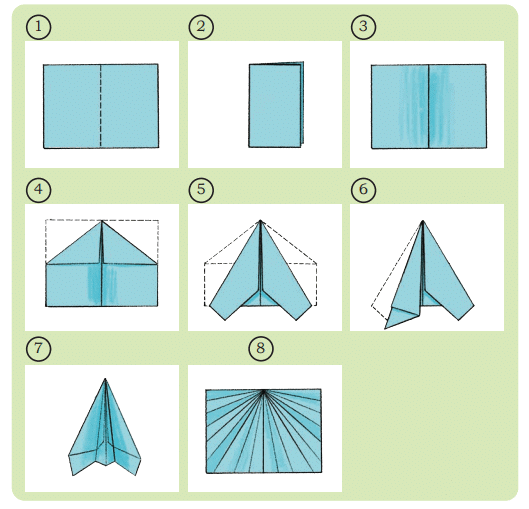
(a) Mark the line of symmetry in Fig. 3, Fig. 4, and Fig. 5.
Ans: 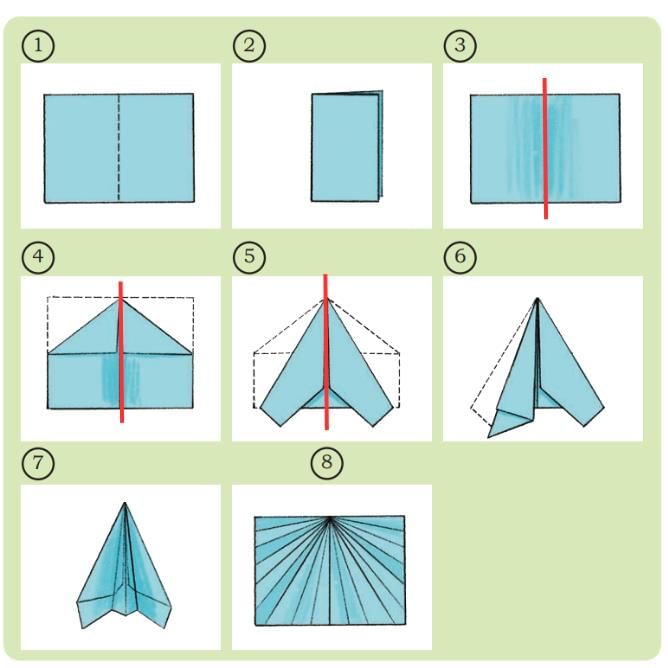
(b) How many lines of symmetry can you see in Fig. 8?
Ans: 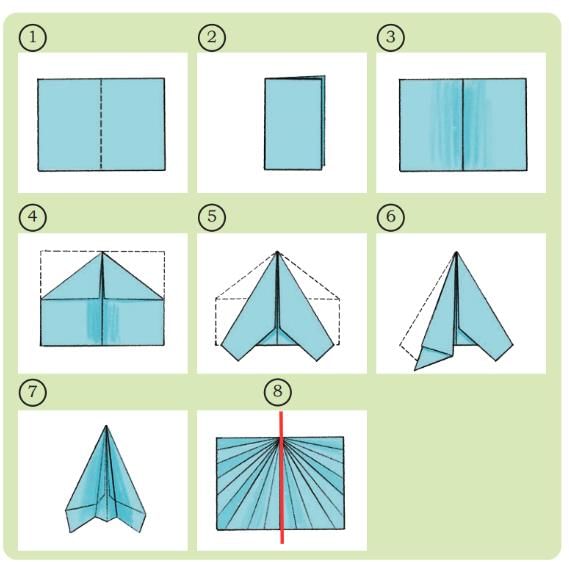
One line of symmetry.
(c) Where will you place a mirror to see the reflection of the right half side of Fig. 8? Will it look the same as the left half side?
Ans: Place mirror: Along vertical line of symmetry (center).
Reflection: Yes, right half reflects to match left half (symmetrical).
Along center; yes, same.
(d) Fly the plane.
Ans: Action: Follow folding steps and fly the plane.
(e) Will the plane fly if there is no line of symmetry?
Ans: No symmetry: Plane may be unbalanced, affecting flight.
(f) Try to make an asymmetrical plane.
Ans: Fold unevenly (e.g., one wing larger).
Create uneven folds.
(g) Fly both the planes and see which plane flies for a longer time.
Ans: Symmetrical plane: Likely flies longer due to balance.
Asymmetrical plane: May wobble or crash sooner.
Symmetrical plane flies longer.
(h) Share your observations with your friends.
Ans: Observation: Symmetrical plane flies better; asymmetrical plane is unstable.
3. Holes and Cuts
Mini has made this design by folding and cutting paper.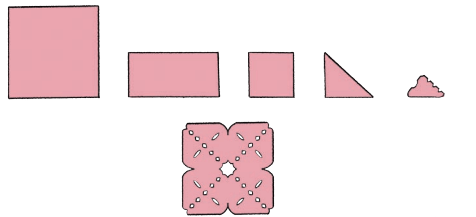
Now it’s your turn! Take a square sheet of paper. Do as instructed below.
Let us see what Rani is making. Rani takes a piece of paper and folds it twice.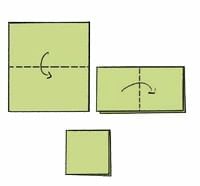
She makes a straight cut at the corner and cuts out two squares on two sides as shown in the picture.
Challenge 1: Where would the hole and cut appear when you open the paper?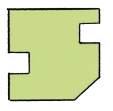 Ans: When the paper will open, the hole and cut appear as follows:
Ans: When the paper will open, the hole and cut appear as follows: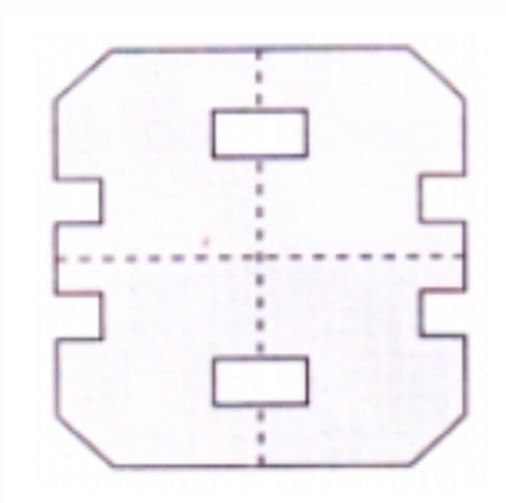
Challenge 2: Fold a piece of paper once; put two cuts in the middle as shown. How many sides will this shape have when you open the folded paper?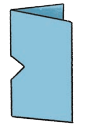 Ans: The shape have 4 sides.
Ans: The shape have 4 sides.
Challenge 3: Fold a paper twice. Where would you cut to make a square hole in the center of the paper? How many cuts are required? Ans: Do it Yourself.
Ans: Do it Yourself.
4. Complete the designs below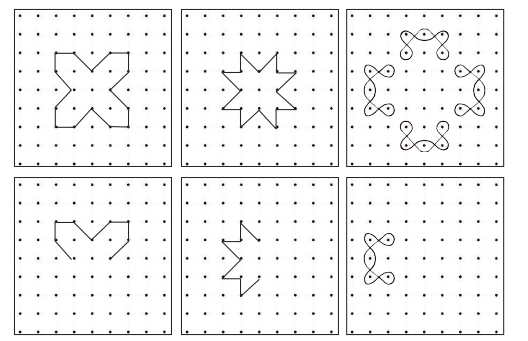 Ans: Do it Yourself.
Ans: Do it Yourself.
Page no. 167
Let Us Do
Symmetry in shapes
Q1: Look at the shapes given along the border. Draw these shapes on the dot grid. Which of the shapes are symmetrical? Draw the lines of symmetry. Ans:
Ans: 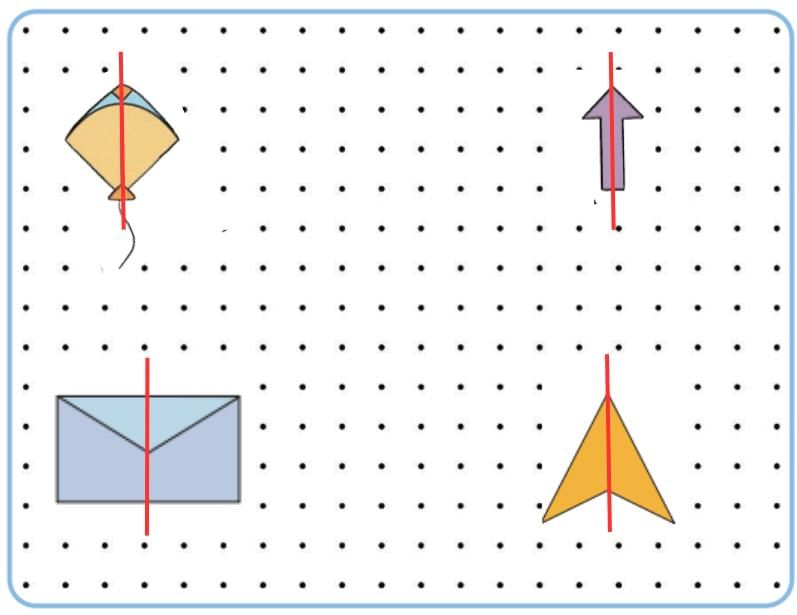
All shapes are symmetrical as by drawing a line of symmetry, it divides the figures into equal parts.
Page 168
Q2: Games with a Mirror
(a) Where should we place the mirror in shape A to get the shapes given below?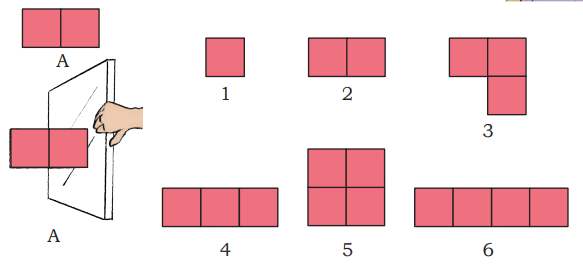
Ans: 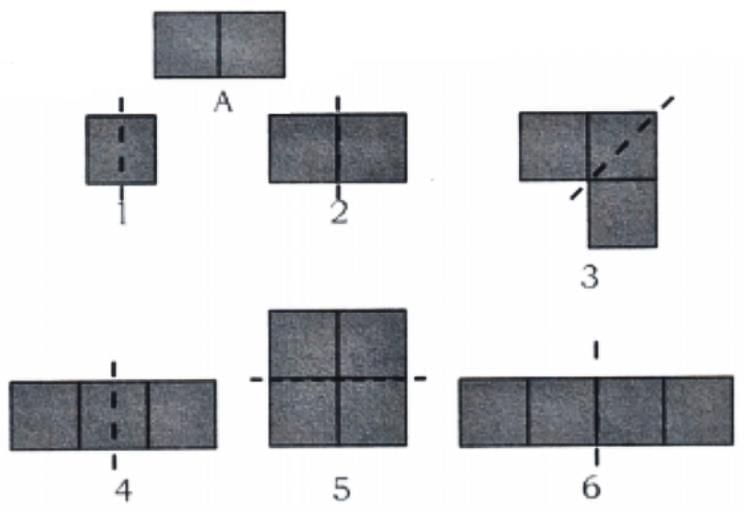
(b) Circle the numbers whose mirror image is the same number.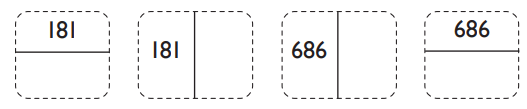 Ans:
Ans: 
Which digits from 0 to 9 have the same mirror image?
Ans: 0, 1 & 8 will have same mirror images and 3 (in some digital fonts).
Make some 4-digit numbers such that the mirror image is the same number. Where would you keep the mirror in each case? How many such numbers can you make?
Ans: Some examples of the 4-digit numbers that have the same mirror images are: 1881, 8118, 1001, 8008, etc. We will keep the mirror to the left or right side of the number in each case.
(c) Make similar questions and ask your friends to guess the numbers.
Ans: Do it Yourself!
Page 169
Q3. What do you notice about the letters written on the ambulance? Why are they written this way? Discuss.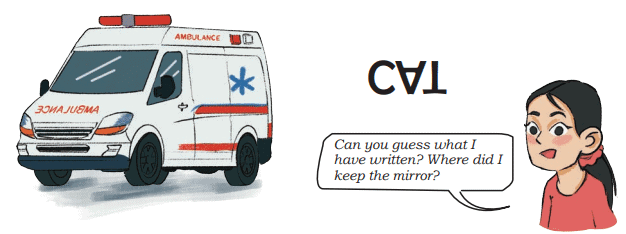 Ans: The word "AMBULANCE" is written backward (like in a mirror) on the front of the ambulance.
Ans: The word "AMBULANCE" is written backward (like in a mirror) on the front of the ambulance.
Why?
So drivers in cars ahead see it correctly in their rearview mirror and move out of the way quickly!

It is written CAT and the mirror has been kept horizontally below the word.
Can you identify these words? Where will you place the mirror to read the following words correctly? Ans:
Ans: 
Now, you try to write some words/names in this way and challenge your friends to guess them.
Ans: Do it Yourself!
Q4. Complete the following to make symmetrical shapes.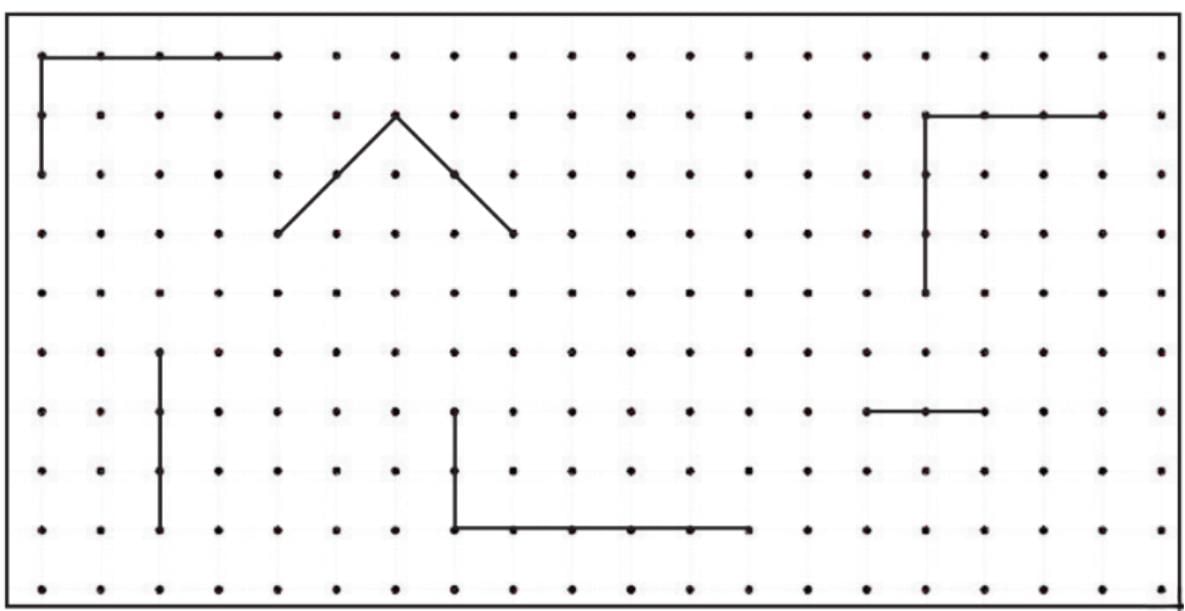
Ans: 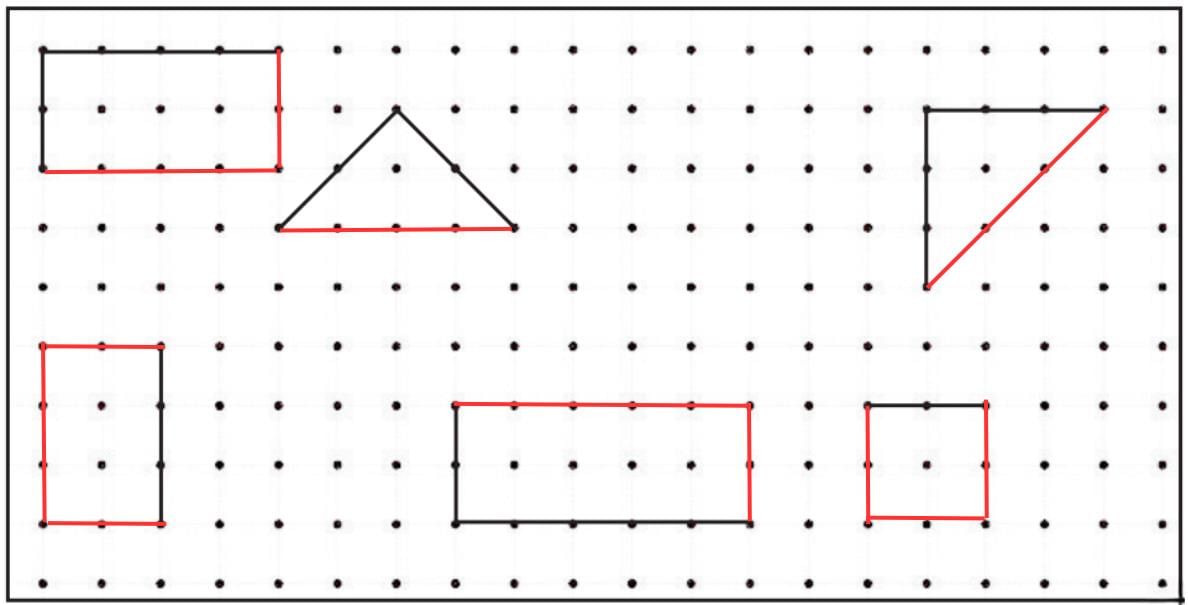
Page 170
Q5: Observe the shapes. How many sides does each shape have?
How many lines of symmetry does each shape have? You may trace these shapes and check the lines of symmetry by folding the shapes.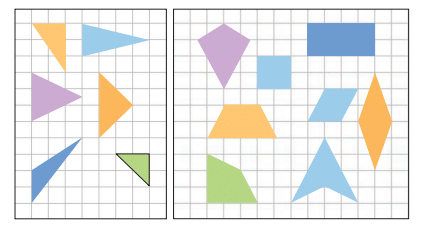 Ans: Do it Yourself!
Ans: Do it Yourself!
Tiling the Tiles
Here are some patterns with tiles. Identify the repeating unit (tile) and continue the patterns.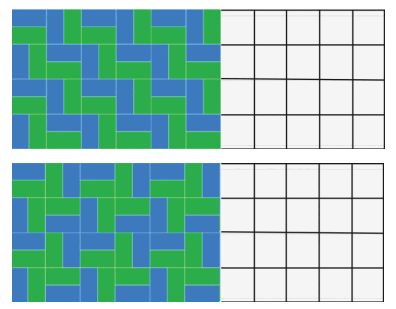 Ans: Do it Yourself!
Ans: Do it Yourself!
Page 171
Tiles at the Tile Shop
Bablu Chacha makes beautiful tiles of the kinds shown below. Design creative tiles of your own in the spaces given below. You may use a rangometry kit or shape cutouts.
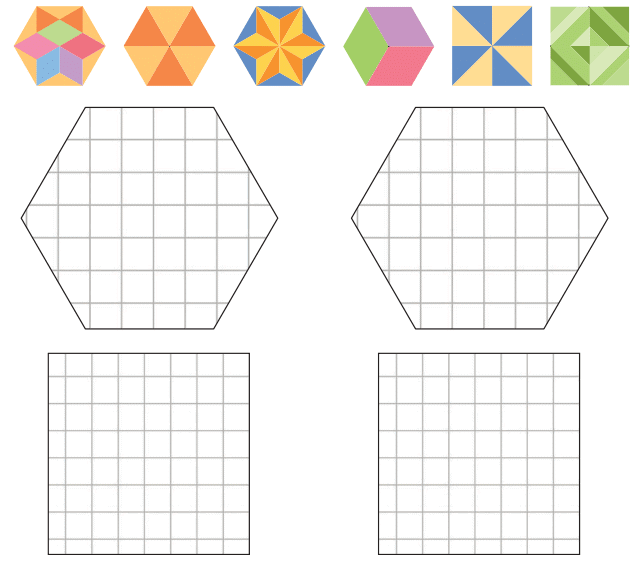
Q1: Which shapes have you used to make the tiles?
Ans: Do it Yourself!
Q2: Which of the tiles are symmetrical? Draw the lines of symmetry (if any).
Ans: 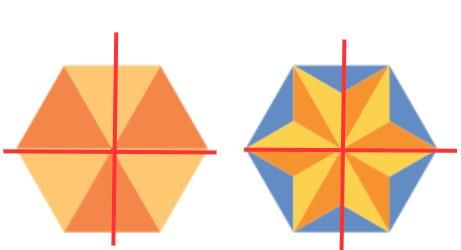
Q3: Make more tiles by joining two or more shapes. Trace them in your notebook to create paths with no gaps or overlaps.
Ans: Do it Yourself!
Q4: Look at the following shapes. What do you notice? Discuss.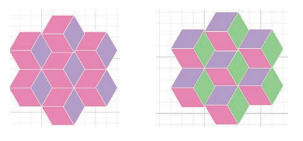 Ans: Both are identical. The difference is of the colour pattern.
Ans: Both are identical. The difference is of the colour pattern.
Page No. 172
Let Us Do
Q1: Make floor patterns with your tile. Mini has made a floor pattern as shown below.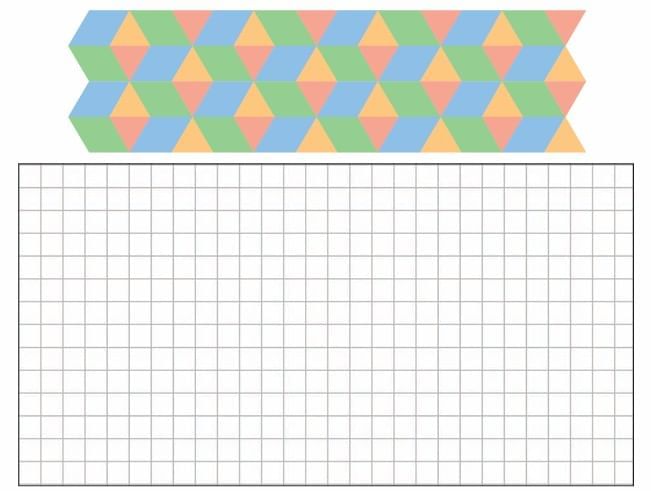 Ans: Do it Yourself!
Ans: Do it Yourself!
Q2: Making a catty wall!
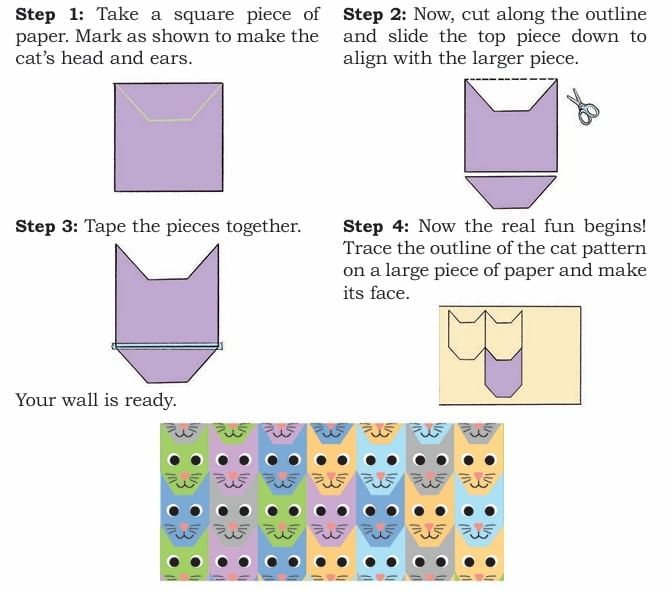
Create more of these tiles. Some ideas to make creative wall patterns are given below.
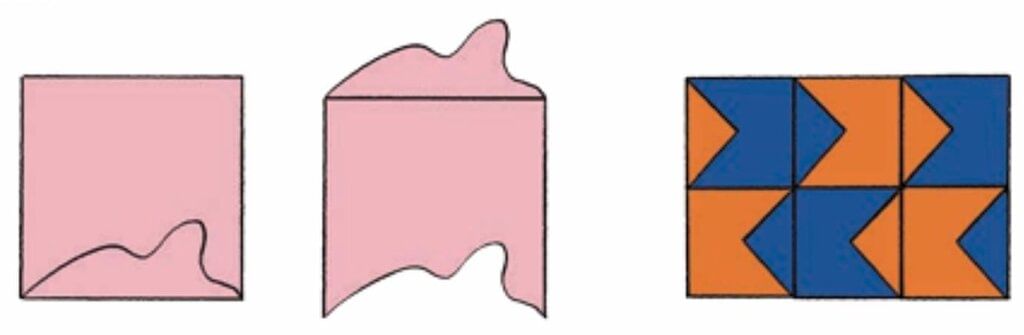
Ans: Do it Yourself!
Q3: Let us go on a nature walk (Project time)
Go for a nature walk to a nearby park or around your school with your teacher or your parents. Observe the patterns, designs, or symmetry around you carefully. Collect leaves, petals, and flowers that have fallen on the ground.
Ans:
|
54 videos|186 docs|14 tests
|
FAQs on NCERT Solutions for Class 4 Maths Chapter 11 - Fun with Symmetry
| 1. What are the key concepts covered in "Let Us Do" from the NCERT Class 4 syllabus? |  |
| 2. How can symmetry be identified in everyday objects as discussed in "Let Us Do"? |  |
| 3. What activities are included in "Let Us Do" to help students learn about symmetry? |  |
| 4. Why is learning about symmetry important for Class 4 students? |  |
| 5. How does "Let Us Do" engage students in understanding geometric shapes? |  |















