NCERT Solutions for Class 4 Maths Chapter 13 - The Transport Museum
| Table of contents |

|
| Page No. 184 |

|
| Page 185 |

|
| Page 186 |

|
| Page No. 188 |

|
| Page No. 190 |

|
| Page 191 |

|
| Page No. 192 |

|
| Page 193 |

|
| Page 194 |

|
| Page 195 |

|
| Page No. 198 |

|
| Page No. 199 |

|
| Page No. 200 |

|
| Page No. 201 |

|
| Page No. 202 |

|
Page No. 184
Mystery Matrix
Q: Fill the yellow boxes with 1-digit numbers (multiplicands and multipliers) such that you get the products given in the white boxes.
Fill the remaining white boxes with appropriate products. 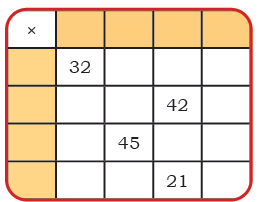
Ans: 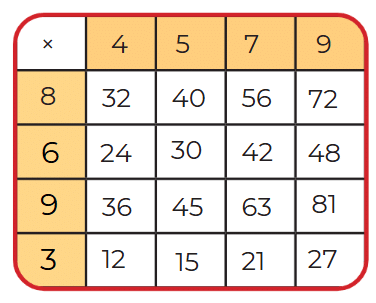
Q: The product of the numbers in each row is given in the orange boxes. The product of the numbers in each column is given in the blue boxes. Identify appropriate numbers to fill the blank boxes.
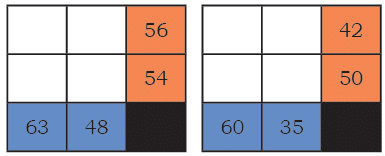 Ans:
Ans:
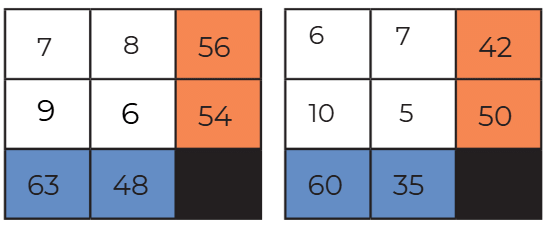
Times 10
Q: Match each problem with the appropriate pictorial representation and write the answer.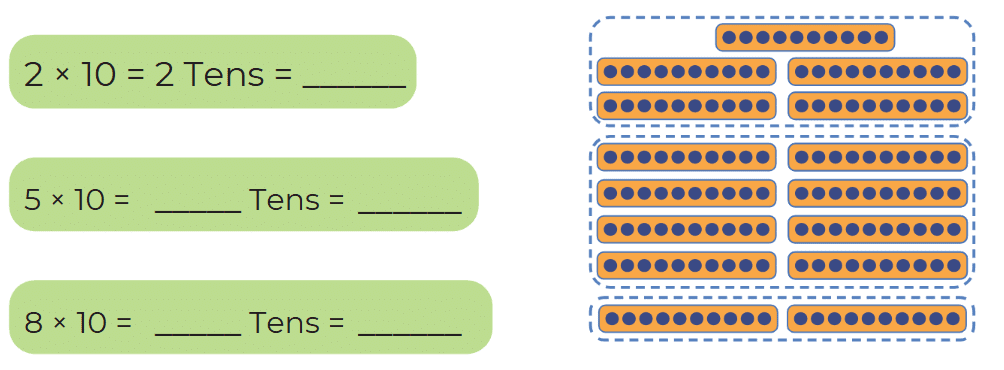
Ans: 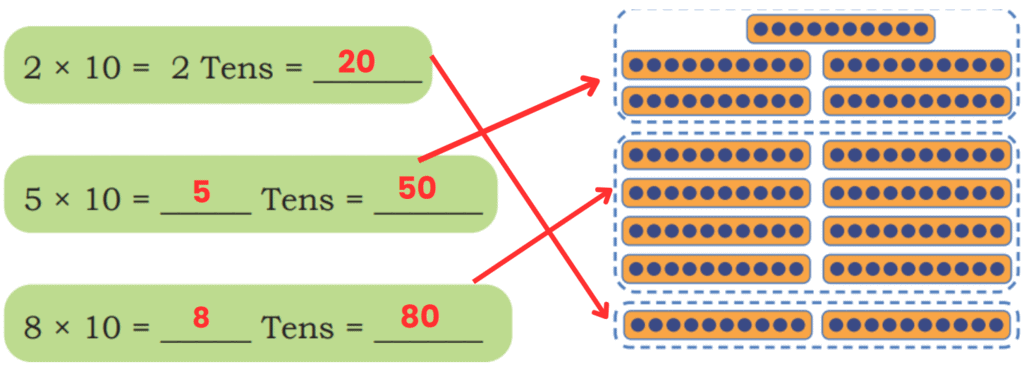
Page 185
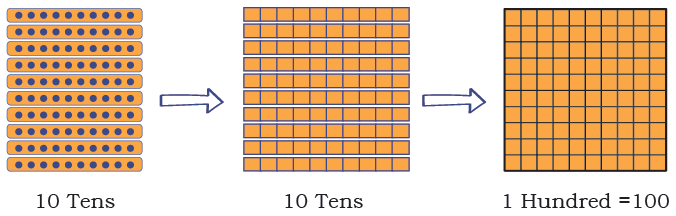 Q: What is 10 × 10 = __________ Tens = __________
Q: What is 10 × 10 = __________ Tens = __________
Ans: 10 × 10 = 10 Tens = 1 Hundred
Constructing Tables
Q: How many pebbles are there in this arrangement? _______
This is a 5 × 15 arrangement. There is an easy way to find this product by splitting the arrangement.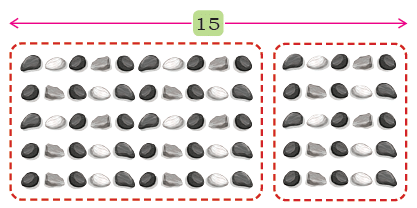 Ans: Let’s break it down:
Ans: Let’s break it down:
5 × 15 can be split as 5 × 10 and 5 × 5.
5 × 10 = 50
5 × 5 = 25
Now add them: 50 + 25 = 75 pebbles.
So, the blanks are filled as: 5 × 15 = 5 × 10 and 5 × 5 = 50 + 25 = 75 pebbles.
Page 186
Recall the times-tables that we created in Grade 3. Now construct a times-15 table. You may use the arrangement given below and split the columns into 10 and 5 for ease of counting, as shown on the previous page.
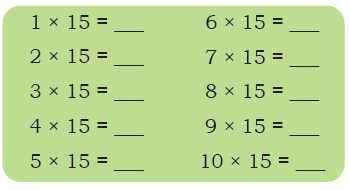 Ans:
Ans:
1 × 15 = (1 × 10 + 1 × 5) = 10 + 5 = 15
2 × 15 = (2 × 10 + 2 × 5) = 20 + 10 = 30
3 × 15 = (3 × 10 + 3 × 5) = 30 + 15 = 45
4 × 15 = (4 × 10 + 4 × 5) = 40 + 20 = 60
5 × 15 = (5 × 10 + 5 × 5) = 50 + 25 = 75
6 × 15 = (6 × 10 + 6 × 5) = 60 + 30 = 90
7 × 15 = (7 × 10 + 7 × 5) = 70 + 35 = 105
8 × 15 = (8 × 10 + 8 × 5) = 80 + 40 = 120
9 × 15 = (9 × 10 + 9 × 5) = 90 + 45 = 135
10 × 15 = (10 × 10 + 10 × 5) = 100 + 50 = 150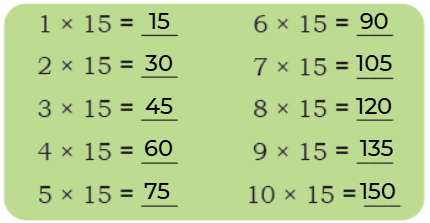
Q1: What patterns do you see in this table?
Ans: Each answer is 15 more than the last:
Start at 15, then 30, 45, 60, 75, ...
1 × 15 = 15, the number of pebbles in the first row.
2 × 15 = 15 + 15 = 30 i.e., the number of pebbles in the both first and second row
3 × 15 = 15 + 15 + 15 = 45, i.e., the number of pebbles in the first three rows
The last digit alternates between 5 and 0:
15 (5), 30 (0), 45 (5), 60 (0), ...
Q2: Compare the times-15 table with the times-5 table. What similarities and differences do you notice?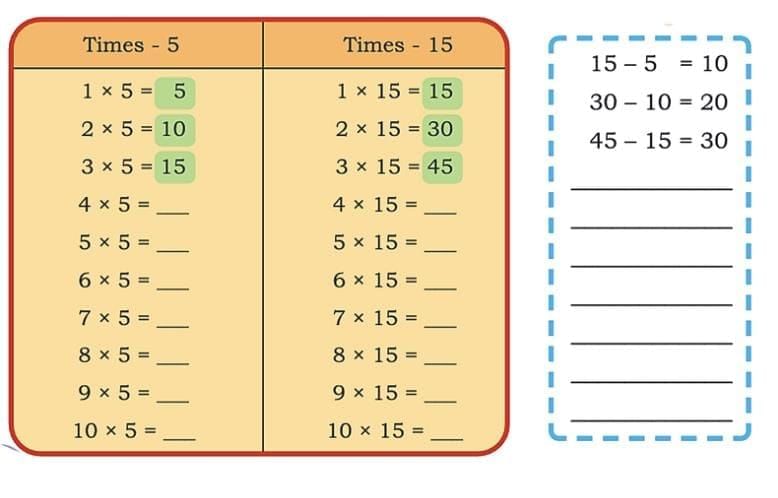 Ans:
Ans: 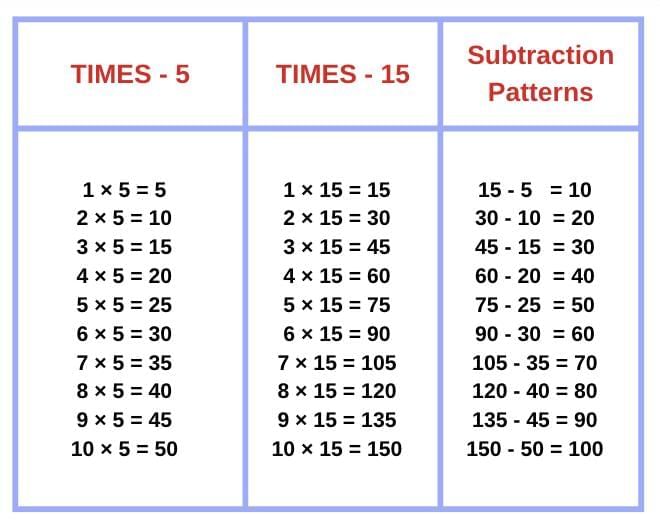
Similarity:
1. They follow a pattern:
In the 5-times table, numbers go up by 5 each time.
In the 15-times table, numbers go up by 15 each time.
2. Increae in the difference
The subtraction answers increase by 10 each time:
10, 20, 30, 40, 50...
Difference:
- Each successive number in the times-15 table is three times larger than the corresponding number in the times-5 table.
Q3: Construct other times-tables for numbers from 11 to 20, as you did for 15.
Ans: To make times-tables from 11 to 20, multiply each number by 1, 2, 3, up to 10.
For example:
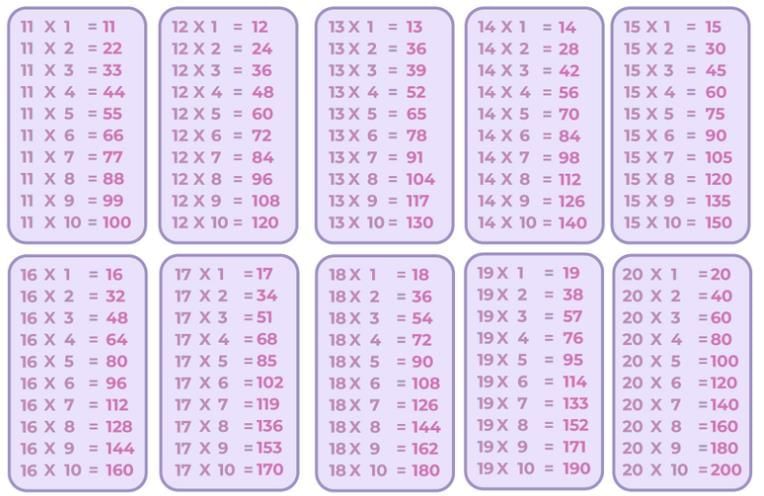
Q4: As you compared the times-5 table with the times-15 table, compare the times-1 table with the times-11 table, the times-2 table with the times-12 table, and so on. Share your observations.
Ans: 1. Times-1 vs. Times-11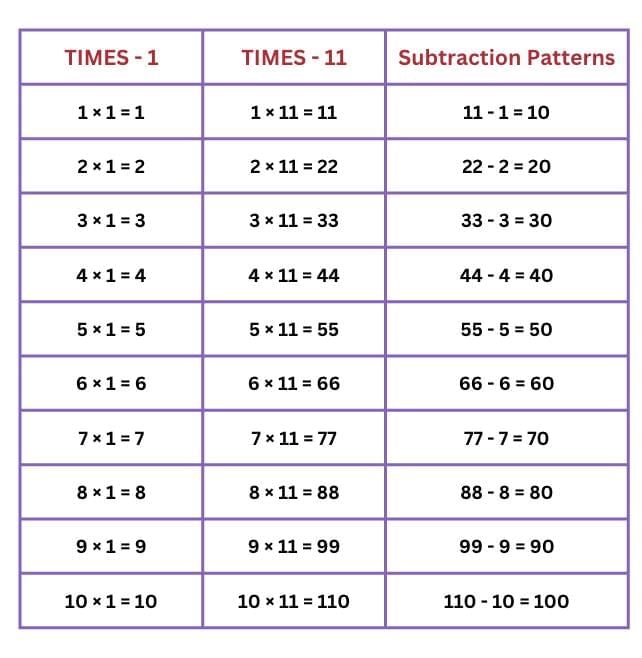
2. Times-2 vs. Times-12
3. Times-3 vs. Times-13
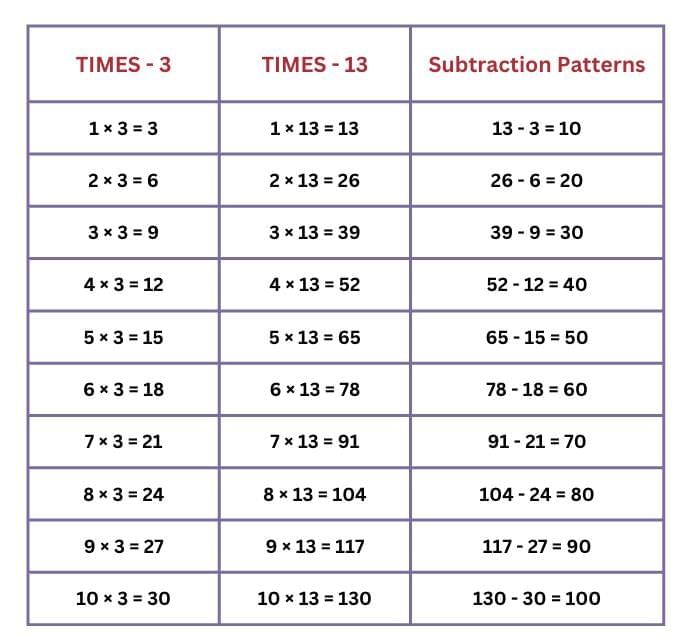
...... repeat the same for 14, 15, 16, 17, 18, 19 and 20
Here is an arrangement of wheels. To count the total number of wheels, Tara splits them into two equal groups.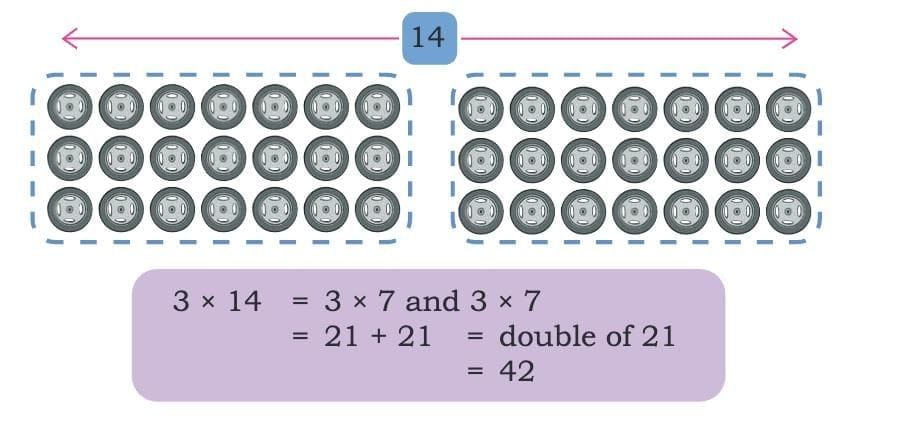
Similarly, 6 × 14 can be obtained by splitting the arrangement into two equal groups.
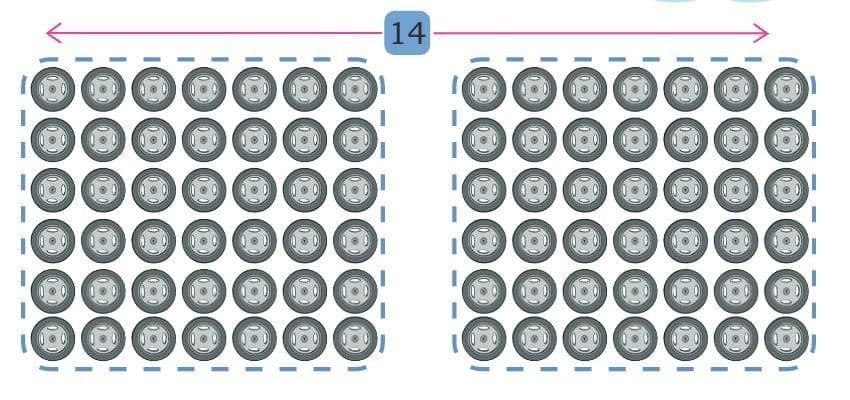
6 × 14 = 6 × 7 and 6 × 7
= 42 + 42 = double of 42
= 84
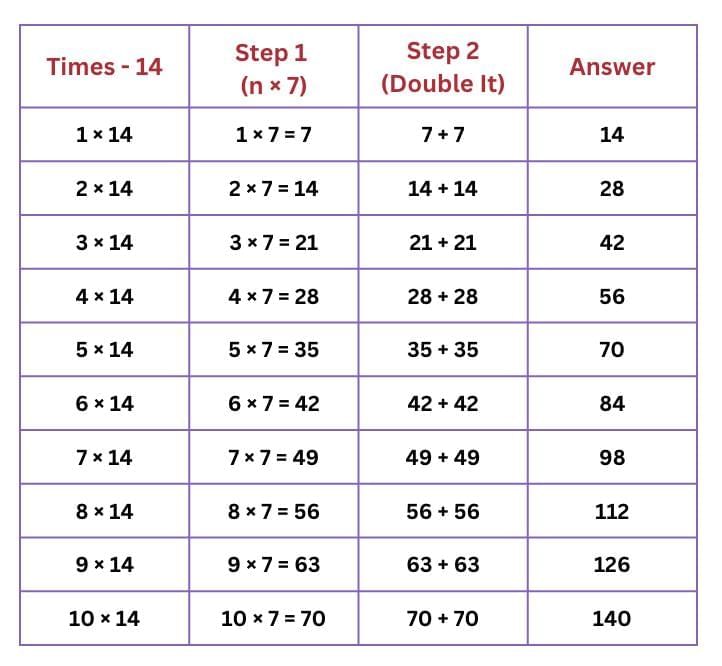
We have seen how to calculate 3 × 14 and 6 × 14 by splitting and doubling. Can we construct the times-14 table by splitting and doubling? Try!
Solution:
Yes, we can construct the times-14 table by splitting and doubling.
What other times tables can be constructed by splitting into equal groups and doubling? Give examples.
Solution:
We can construct 8, 10, 12, 16, 18, 20, etc. times tables by splitting into equal groups and doublings.
Page No. 188
Multiples of 10
Find the answers to the following:
(a) 15 × 10 = _____ Tens = _____
Ans: 15 × 10 = 15 Tens
= 10 Tens + 5 Tens
= 100 + 50 = 150
(b) 16 × 10 = _____ Tens = _____
Ans: 16 × 10 = 16 Tens
= 10 Tens + 6 Tens
= 100 + 60 = 160
(c) 19 × 10 = _____ Tens = _____
Ans: 19 × 10 = 19 Tens
= 10 Tens + 9 Tens
= 100 + 90 = 190
(d) 20 × 10 = _____ Tens = _____
Ans: 20 × 10 = 20 Tens
= 10 Tens + 10 Tens
= 100 + 100 = 200
Now think and answer the following problems.
30 × 10 = _____
Ans: 30 × 10 = 30 Tens = 300
40 × 10 = _____
Ans: 40 × 10 = 40 Tens = 400
70 × 10 = _____
Ans: 70 × 10 = 70 Tens = 700
50 × 10 = _____
Ans: 50 × 10 = 50 Tens = 500
60 × 10 = _____
Ans: 60 × 10 = 60 Tens = 600
80 × 10 = _____
Ans: 80 × 10 = 80 Tens = 800
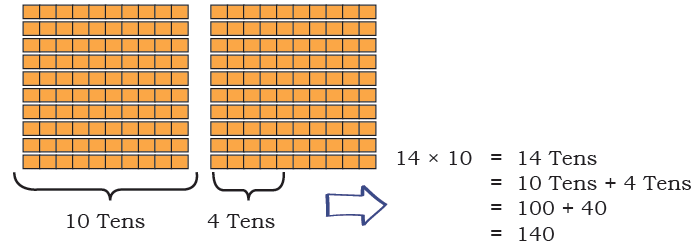
Q: Let us find the number of people who can be in the 26 tempo travellers. 26 × 10 = ________
Ans: 
Q: Answer the following questions. Share your thoughts.
(a) 21 × 10 = _____
Ans: 21 × 10 = 21 Tens = 20 Tens + 1 Ten
= 200 + 10
= 210
(b) 42 × 10 = _____
Ans: 42 × 10 = 42 Tens = 40 Tens + 2 Tens
= 400 + 20
= 420
(c) 65 × 10 = _____
Ans: 65 × 10 = 65 Tens = 60 Tens + 5 Tens
= 600 + 50
= 650
(d) 38 × 10 = _____
Ans: 38 × 10 = 38 Tens = 30 Tens + 8 Tens
= 300 + 80
= 380
(e) 53 × 10 = _____
Ans: 53 × 10 = 53 Tens = 50 Tens + 8 Tens
= 500 + 30
= 530
(f ) 87 × 10 = _____
Ans: 87 × 10 = 87 Tens = 80 Tens + 7 Tens
= 800 + 70
= 870
Q: A small bus can seat 20 people. How many people can be seated in 12 buses?
Now let us do 12 × 20.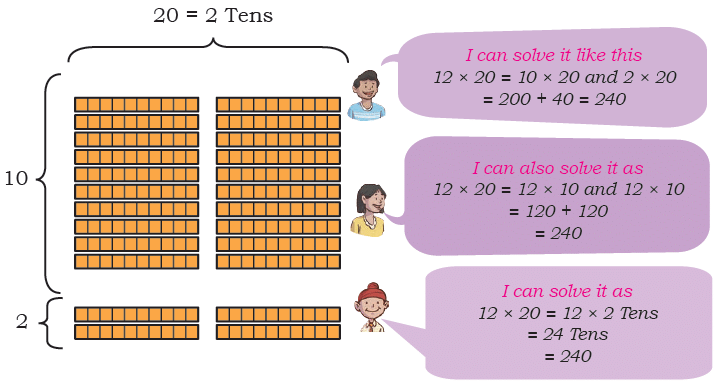 Solve the following problems. Share your thoughts.
Solve the following problems. Share your thoughts.
Q: 24 × 40 = _______
Ans: First, break 24 into 20 + 4.
Then, 20 × 40 = 800 and 4 × 40 = 160.
Add them: 800 + 160 = 960.
So, 24 × 40 = 960.
Q: 50 × 60 = _______
Ans: 50 × 60 means 5 tens × 6 tens.
So, 5 × 6 = 30, then 30 × 100 = 3000.
So, 50 × 60 = 3000.
Q: 13 × 30 = _______
Ans: Break 13 into 10 + 3.
Then, 10 × 30 = 300 and 3 × 30 = 90.
Add them: 300 + 90 = 390. So, 13 × 30 = 390.
Q: 43 × 60 = _______
Ans: Break 43 into 40 + 3.
Then, 40 × 60 = 2400 and 3 × 60 = 180.
Add them: 2400 + 180 = 2580.
So, 43 × 60 = 2580.
Q: 70 × 80 = _______
Ans: 70 × 80 means 7 tens × 8 tens. So, 7 × 8 = 56, then 56 × 100 = 5600. So, 70 × 80 = 5600.
Page No. 190
A Day at the Transport Museum
Amala, Raahi and Farzan are visiting the “Transport Museum”. This museum has a collection of different modes of transport used by people in India. It includes several vehicles from the olden days. Raahi spots a toy train. She figures out that each coach can seat 14 children. The toy train has 15 coaches.
Q: How many children can be seated in the toy train?
Ans: 15 × 14 = (10 × 10) + (10 × 4) + (5 × 10) + (5 × 4) = 100 + 40 + 50 + 20 = 210. 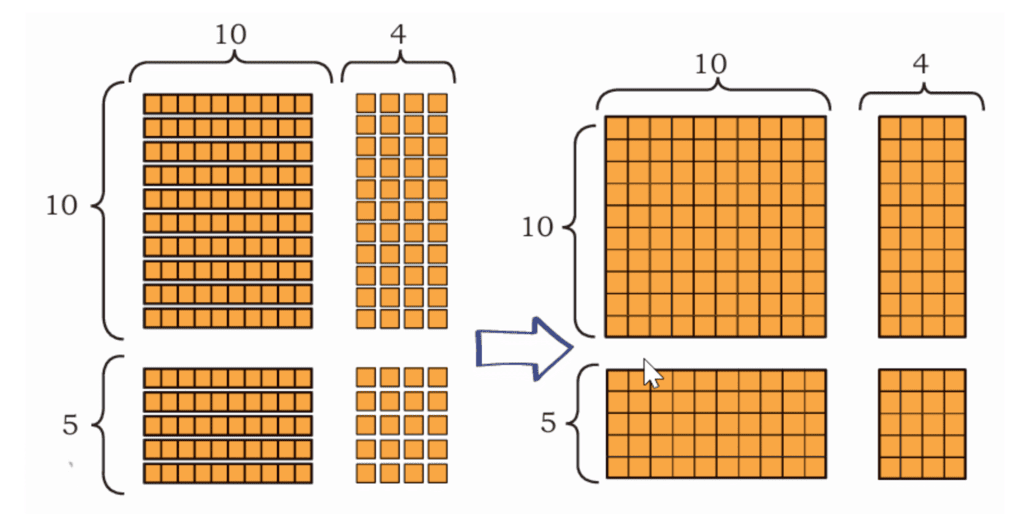

Page 191
Q: She wonders how many coaches will be needed for the 324 children from her school. Remember, each coach can seat only 14 children.
Ans: 324 ÷ 14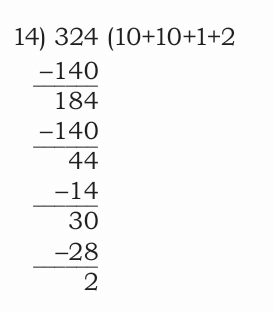
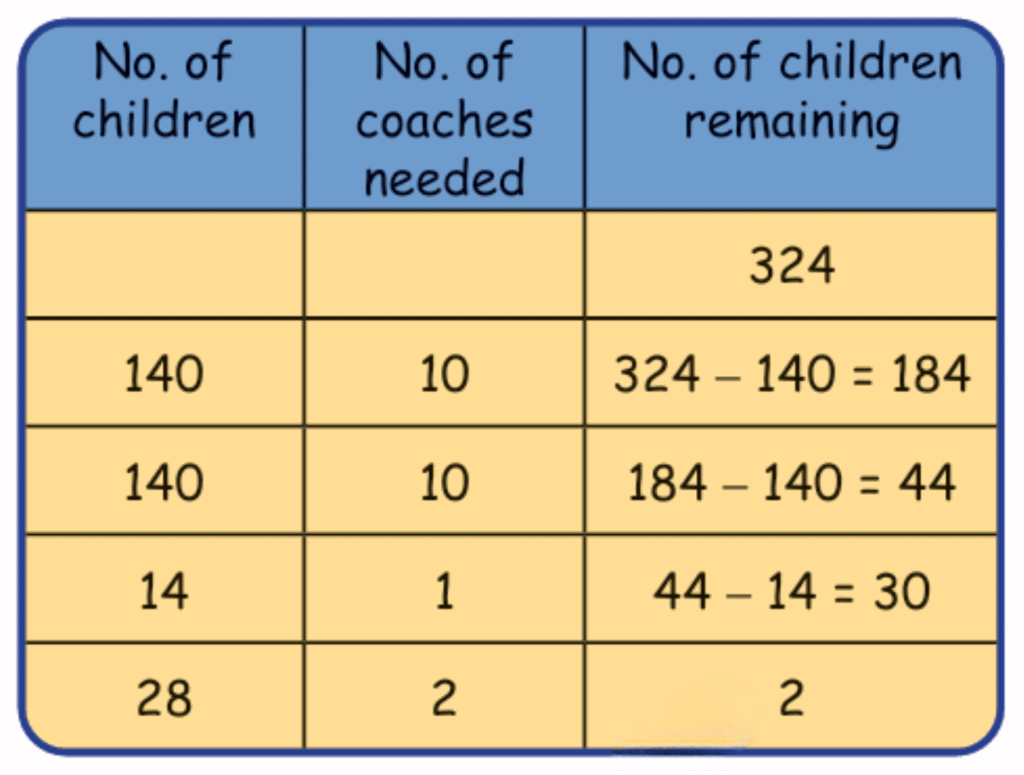
Ans: 23 coaches, 2 children remain (need 24th coach).
Page No. 192
Let Us Solve
Q: Also, identify remainder (if any) in the division problems.
(a) 25 × 34
Ans: 
(b) 16 × 43
Ans: 
(c) 68 × 12
Ans: 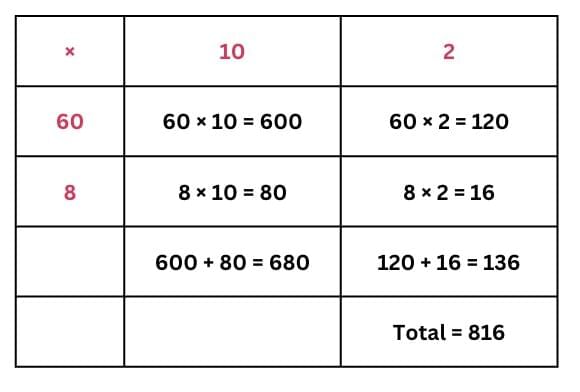
(d) 39 × 13
Ans: 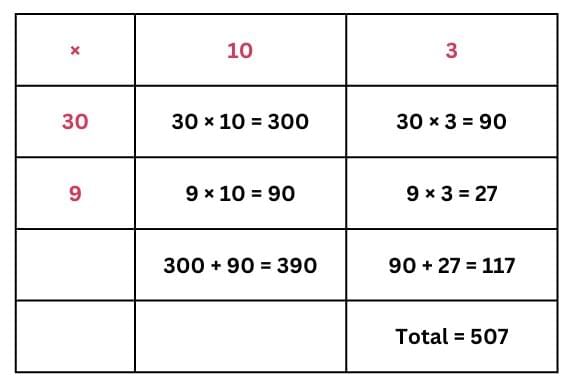
(e) 125 ÷ 15
Ans: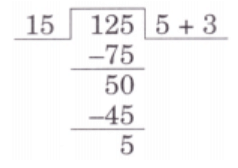 Thus, when 125 is divided by 15, we get (5 + 3) = 8 with remainder 5.
Thus, when 125 is divided by 15, we get (5 + 3) = 8 with remainder 5.
(f) 94 ÷ 11
Ans:  Thus, when 94 is divided by 11, we get (2 + 3 + 3) = 8 with remainder 6.
Thus, when 94 is divided by 11, we get (2 + 3 + 3) = 8 with remainder 6.
(g) 440 ÷ 22
Ans: 
So, 440 ÷ 22 = 10 + 10 = 20
(h) 508 ÷ 18
Ans:  Thus, when 508 is divided by 18, we get (10 + 10 + 5 + 3) = 28 with remainder 4.
Thus, when 508 is divided by 18, we get (10 + 10 + 5 + 3) = 28 with remainder 4.
Multiples of 100
Q: 2 × 100 = 2 Hundreds = 200
3 × 100 = ______ Hundreds = ______
Ans: 3 × 100 = 3 Hundreds = 300
5 × 100 = ______ = ______
Ans: 5 × 100 = 5 Hundreds = 500
8 × 100 = ______ = ______
Ans: 8 × 100 = 8 Hundreds = 800


Ans: 10 × 100 = 10 Hundreds = 1000:
11 × 100 = 11 Hundreds
= 10 Hundreds + 1 Hundred
= 1000+ 100 = 1100
12 × 100 = _________
Ans: 12 × 100 = 12 Hundreds
= 10 Hundreds + 2 Hundreds
= 1000 + 200 = 1200
15 × 100 = _________
Ans: 15 × 100 = 15 Hundreds
= 10 Hundreds + 5 Hundreds
= 1000 + 500 = 1500
20 × 100 = _______
Ans: 20 × 100 = 20 Hundreds
= 10 Hundreds + 10 Hundreds
= 1000 + 1000 = 2000
27 × 100 = _______
Ans: 27 × 100 = 27 Hundreds
= 20 Hundreds + 7 Hundreds
= 2000 + 700 = 2700
70 × 100 = _______
Ans: 70 × 100 = 70 Hundreds
= 7000
Page 193
Q: Now answer the following questions. Share your thoughts.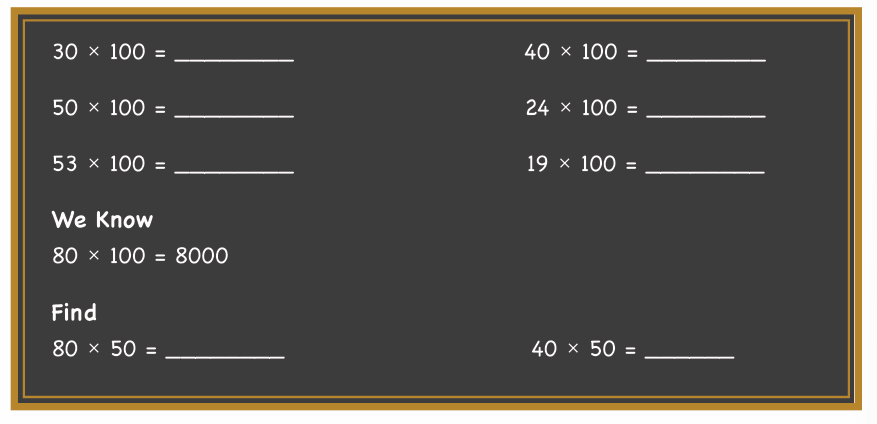
30 × 100 =
30 × 100 = 30 Hundreds
= 3000
40 × 100 =
40 × 100 = 40 Hundreds
= 4000
50 × 100 =
50 × 100 = 50 Hundreds
= 5000
24 × 100 =
24 × 100 = 24 Hundreds
= 20 Hundreds + 4 Hundreds
= 2000 + 400 = 2400
53 × 100 =
53 × 100 = 53 Hundreds
= 50 Hundreds + 3 Hundreds
= 5000 + 300 = 5300
19 × 100 =
19 × 100 = 19 Hundreds
= 10 Hundreds + 9 Hundreds
= 1000 + 900 = 1900
We know:
80 × 100 = 8000
Find: 80 × 50 =
80 × 50 = 80 × (100 ÷ 2)
= (80 × 100) ÷ 2
= 8000 ÷ 2
= 4000
40 × 50 =
40 × 50 = 40 × (100 ÷ 2)
= (40 × 100) ÷ 2
= 4000 ÷ 2
= 2000
Page 194
Q: Let us find 11 × 200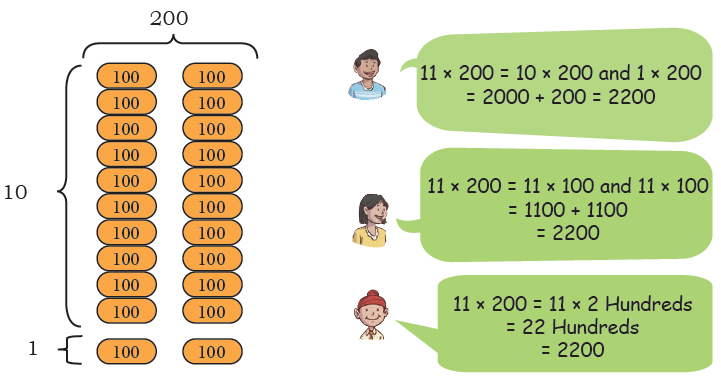 Ans: 11 × 200 = 11 × 2 × 100 = 22 × 100 = 2200.
Ans: 11 × 200 = 11 × 2 × 100 = 22 × 100 = 2200.
Q: Share what you notice about the answers to these problems.
11 × 100 = __________
Ans: 11 × 1 Hundred = 11 Hundreds = 1100
22 × 100 = __________
Ans: 22 × 1 Hundred = 22 Hundreds = 2200
11 × 200 = __________
Ans: 11 × 2 Hundreds = 22 Hundreds = 2200
22 × 200 = __________
Ans: 22 × 2 Hundreds = 44 Hundreds = 4400
Q: Answer the following questions. Share your thoughts.
18 × 100 = ________
Ans: 18 × 1 Hundred = 18 Hundreds = 1800
15 × 200 = ________
Ans: 15 × 200 = 15 × 2 Hundreds
= 30 Hundreds
= 3000
23 × 200 = ________
Ans: 23 × 200 = 23 × 2 Hundreds
= 46 Hundreds
= 4600
5 × 500 = ________
Ans: 5 × 500 = 5 × 5 Hundreds
= 25 Hundreds
= 2500
14 × 300 = ________
Ans: 14 × 300 = 14 × 3 Hundreds
= 42 Hundreds
= 4200
7 × 800 = ________
Ans: 7 × 800 = 7 × 8 Hundreds
= 56 Hundreds
= 5600
Page 195
Q: Find the answers in Set A. Examine the relationships between the problems and the answers in Set A carefully. Then use this understanding to find the answers in Set B.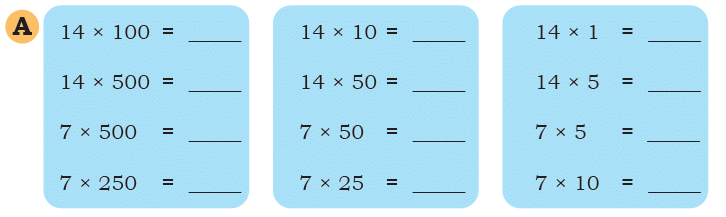
Ans: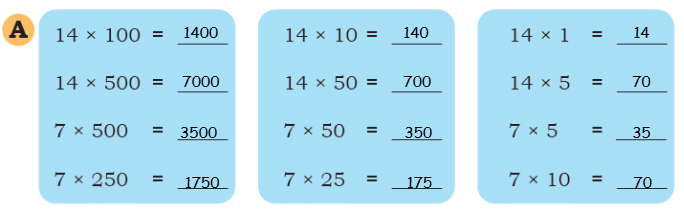
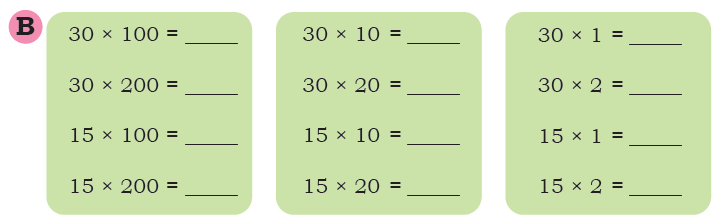
Ans: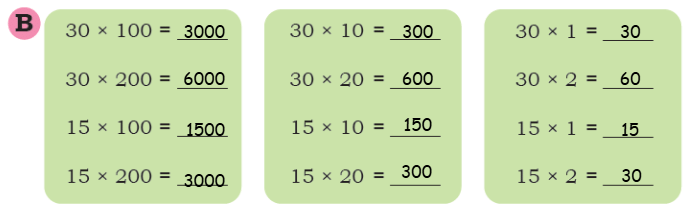

Ans: 
Let Us Solve
Q: Also, identify remainder (if any) in the division problems.
(a) 237 × 28
Ans: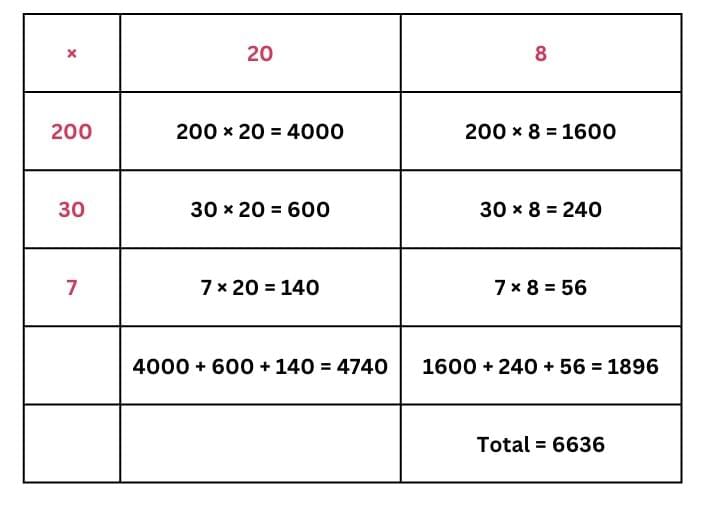
(b) 140 × 16
Ans: 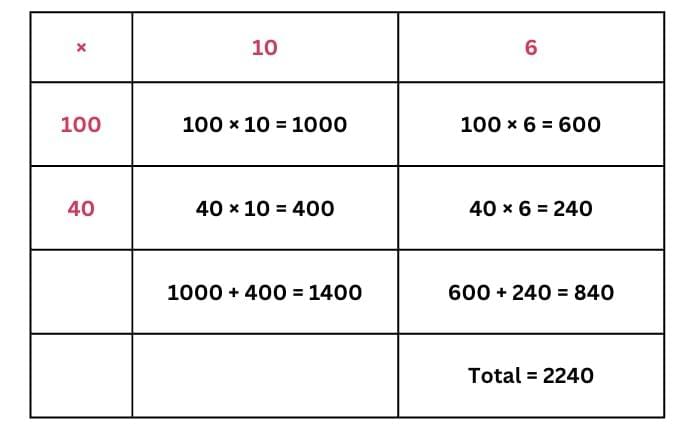
(c) 389 × 57
Ans: 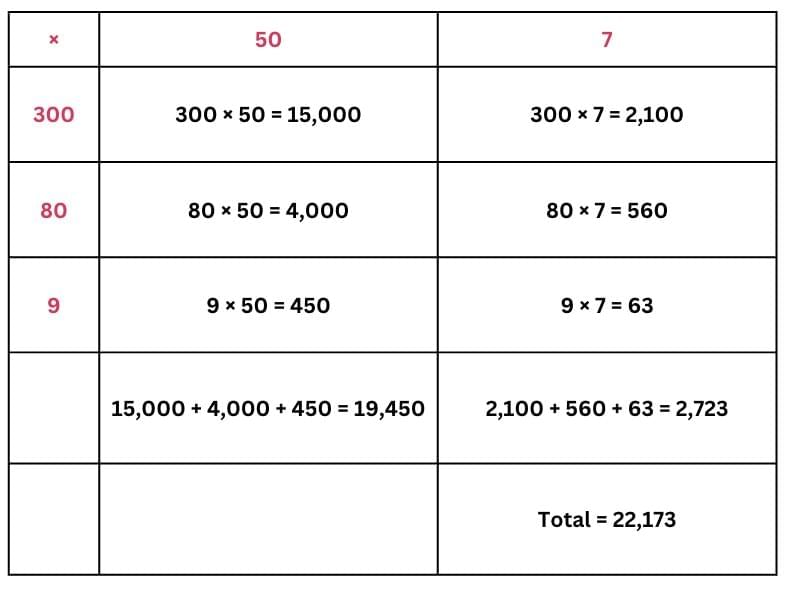
(d) 807 ÷ 24
Ans:  When 807 is divided by 24, we get 10 + 10 + 10 + 2 + 1 = 33, with remainder 15.
When 807 is divided by 24, we get 10 + 10 + 10 + 2 + 1 = 33, with remainder 15.
(e) 692 ÷ 33
Ans:  When 692 is divided by 33, we get 10 + 10 = 20, with remainder 32.
When 692 is divided by 33, we get 10 + 10 = 20, with remainder 32.
(f) 996 ÷ 45
Ans:  When 996 is divided by 45, we get 10 + 10 + 2 = 22, with remainder 6.
When 996 is divided by 45, we get 10 + 10 + 2 = 22, with remainder 6.
Dividing by 10 and 100
Q: A farmer packs his rice in sacks of 10 kg each.
(a) If he has 60 kg of rice, how many sacks does he need?
Ans: Each sack holds 10 kg of rice.
So we divide:
60 ÷ 10 = 6
⇒ He needs 6 sacks.
(b) If he has 600 kg of rice, how many sacks does he need?
Ans: Each sack holds 10 kg of rice.
So we divide:
600 ÷ 10 = 60
⇒ He needs 60 sacks.

Ans: Each sack holds 100 kg of rice.
So we divide:
600 ÷ 100 = 6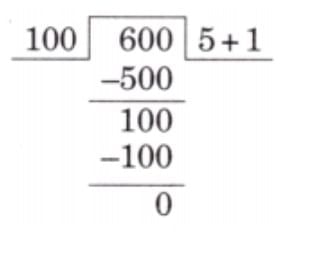
⇒ He needs 6 sacks.
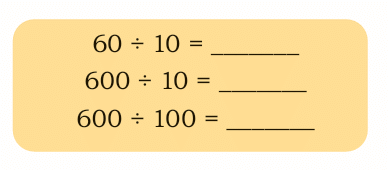
Ans:
60 ÷ 10 = 6 sacks
600 ÷ 10 = 60 sacks
600 ÷ 100 = 6 sacks
Page No. 198
Q: Find the answers to the following questions. Share your thoughts in grade.
40 ÷ 10 = _________
Ans: 40 ÷ 10 = 4
400 ÷ 10 = _________
Ans: 400 ÷ 10 = 40
400 ÷ 100 = _________
Ans: 400 ÷ 100 = 4
4 ÷ 2 = _________
Ans: 4 ÷ 2 = 2
40 ÷ 20 = _________
Ans: 40 ÷ 20 = 2
400 ÷ 200 = _________
Ans: 400 ÷ 200 = 2
Think and answer. Write the division statement in each case.
Q1. Manku the monkey sees 870 bananas in the market. Each bunch has 10 bananas. How many bunches are there in the market?
Ans: Total bananas in the market = 870
Number of bananas in each bunch = 10
Number of bunches in the market = 870 ÷ 10 = 87
Division statement: 870 ÷ 10 = 87
Q2. Rukhma Bi wants to distribute ₹1000/- equally among her 10 grandchildren on the occasion of Eid. How much money will each of them get?
Ans: Number of grandchildren of Rukhma Bi = 10
Amount distributed by Rukhma Bi = ₹ 1000
Amount of money received by each grandchild = ₹ 1000 ÷ 10 = ₹ 100
Division statement: 1000 ÷ 10 = 100
Let Us Solve
Q1: The oldest long-distance train of the Indian Railways is the Punjab Mail which ran between Mumbai and Peshawar. Its first journey was on 12 October 1912. Do you know how many coaches it had on its first journey? It had 6 coaches: 3 carrying 96 passengers and 3 for goods.
(a) How many people travelled in each coach on the first journey?
(b) This train has been running for 106 years now. It runs between Mumbai, Maharashtra and Ferozepur, Punjab. It has 24 coaches. Each coach can carry 72 passengers. How many people can travel on this train?
Ans: (a) Number of coaches carrying passengers in train = 3
Number of peoples in train = 96
People travelled in each coach = 96 ÷ 3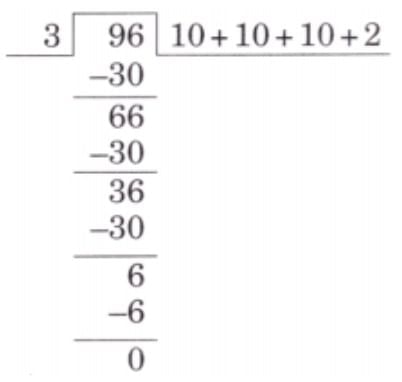
96 ÷ 3 = 10 + 10 + 10 + 2 = 32
Thus, 32 people travelled in each coach.
⇒ 32 people travelled in each passenger coach.
(b) Number of coaches in train = 24
Number of passengers in each coach = 72
Number of people travel in the train = 24 × 72
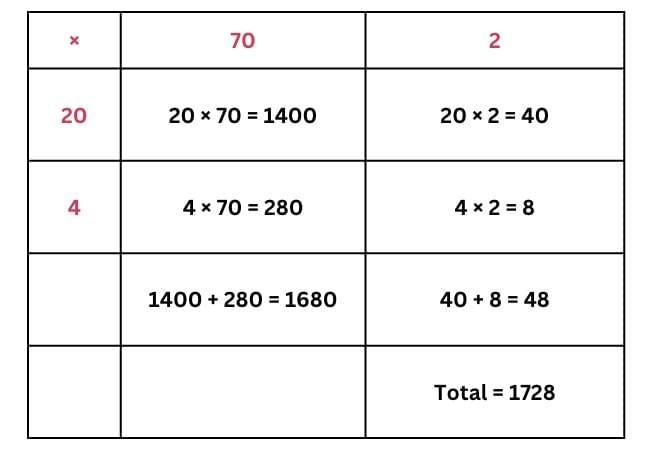
⇒ 1728 people can travel on this train now.
Page No. 199
Q2: Amala and her 35 classmates, along with 6 teachers, are going on a school trip to Goa. They are using the double-decker "hop on hop off" sightseeing bus to explore the city.

(a) 2 people can sit on every seat of the bus. There are 15 seats in the lower deck and 10 in the upper deck. How many seats will they need to occupy? Are there enough seats for everyone?
(b) Find the total cost of the tickets for all children.
(c) What is the cost of the tickets for all teachers?
Ans: (a) Total people: 35 Students + 6 Teachers = 41 people.
Seats needed: 41 ÷ 2 = 20 (1 extra person needs 1 seat).
Total seats: 15 (lower) + 10 (upper) = 25
Yes, there are enough seats for everyone.
Since, the total number of seats is more than the required number of seats occupied.
(b) Ticket price for each child = ₹ 359
Total cost of the tickets for all children = 36 × ₹ 359
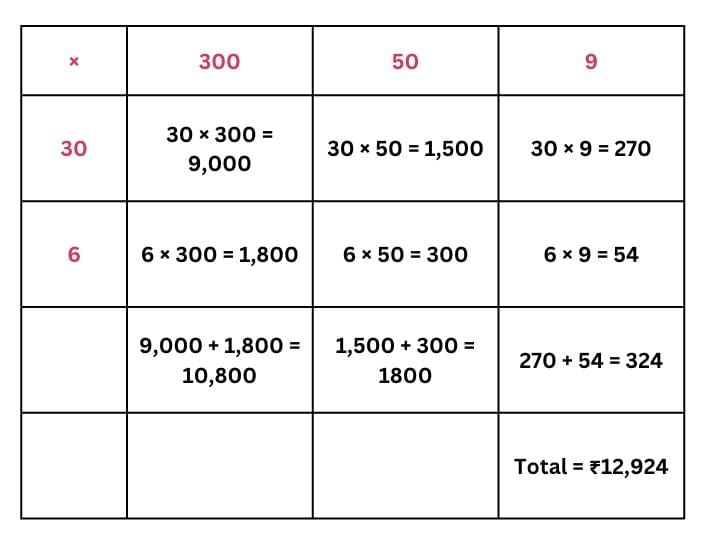 Total coat of tickets for all children = ₹ 12,924
Total coat of tickets for all children = ₹ 12,924
(c) Ticket price for adult = ₹ 899
Total cost of the tickets for all teachers = 6 × ₹ 899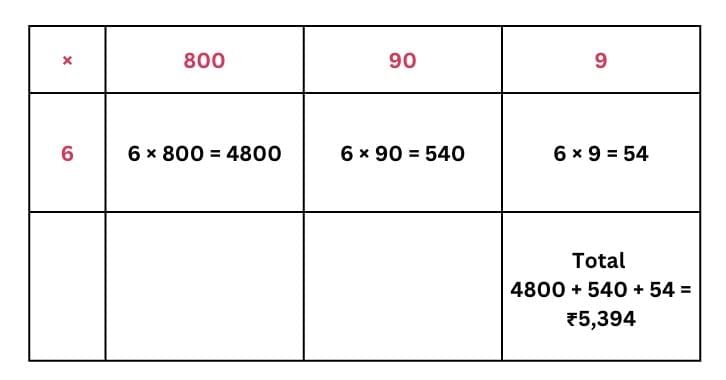
Q3: Kedar works in a brick kiln.
(a) The kiln makes 125 bricks in a day. How many bricks can be made in a month?
(b) Each brick is sold in the market for ₹9. How much money can they earn in a month?
Ans: (a) Assume 30 days
Number of bricks made in a day = 125
So, number of pricks can be made in a month = 30 × 125

⇒ Therefore, 3750 bricks can be made in a month
(b) Price of each brick = ₹ 9
Money earned in a month = ₹ 9 × 3750

Q4: Chilika lake in Odisha is the largest saltwater lake in India. It is famous for the Irrawaddy dolphins. Boats can be hired to go see the dolphins. The trip from Puri includes a bus ride followed by a boat ride. Eight people will be going on the trip.
- A bus ticket from Puri to Satapada costs ₹60.
- A two-hour boat ride for 8 people costs ₹1200.
- How much money do we need to spend on each person?
Ans: Bus: 8 × 60 = 480.
Boat: 1200 (total).
Total: 480 + 1200 = 1680.
Per person: 1680 ÷ 8 = 210.
₹210 per person.
Page No. 200
Q5: Find the multiplication and division sentences below. Shade the sentences. How many can you find?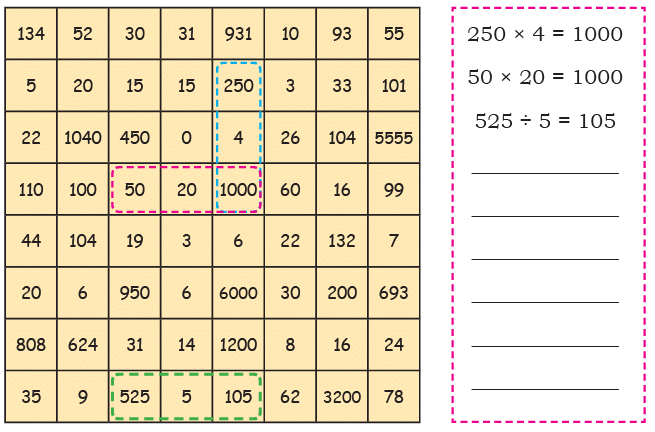
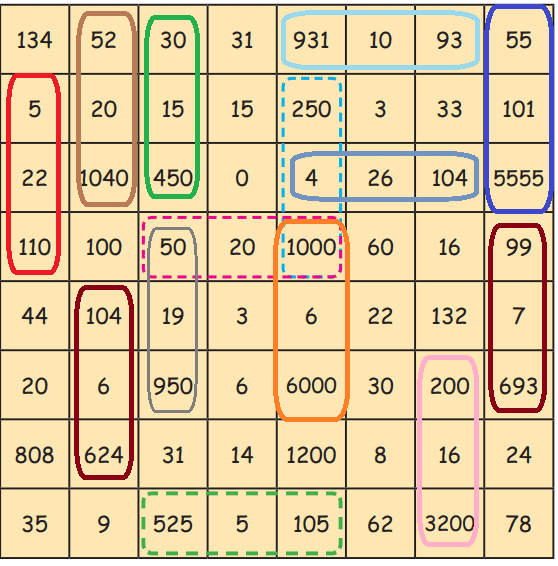
250 × 4 = 1000
50 × 20 = 1000
5 × 22 = 110
52 × 20 = 1040
104 × 6 = 624
30 × 15 = 450
50 × 19 = 950
1000 × 6 = 6000
55 × 101 = 5555
99 × 7 = 693
200 × 16 = 3200
35 × 9 = 315
931 ÷ 10 = 93
4 × 26 = 104
Q6: Solve

(b) 267 × 38
Ans: 
(c) 498 × 9
Ans: 
(d) 89 × 42
Ans: 
(e) 55 × 23
Ans: 
(f) 345 × 17
Ans: 
Following above table method, we can solve below questions as well.
(g) 66 × 22
Ans: 
(h) 704 × 11
Ans: 
(i) 319 × 26
Ans: 
(j) 459 ÷ 3
Ans: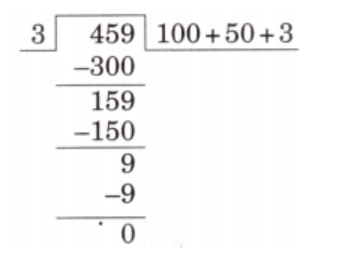
Thus, when 459 is divided by 3, we get 100 + 50 + 3 = 153 with no remainder.
(k) 774 ÷ 18
Ans:
So, 774 + 18 = 10 + 10 + 10 + 10 + 3 = 43
(l) 864 ÷ 26
Ans: 
Thus, when 864 is divided by 26, we get (10 + 10 + 10 + 3 = 33) with remainder 6.
In a similar manner, we can solve remaining questions also.
(m) 304 ÷ 12
Ans:  Thus, when 304 is divided by 12, we get (10 + 10 + 5 = 25) with remainder 4.
Thus, when 304 is divided by 12, we get (10 + 10 + 5 = 25) with remainder 4.
(n) 670 ÷ 9
Ans: 
Thus, when 670 is divided by 9, we get (50 + 20 + 4 = 74) with remainder 4.
(o) 584 ÷ 25
Ans:  Thus, when 584 is divided by 25, we get (10 + 10 + 2 + 1 = 23) with remainder 9.
Thus, when 584 is divided by 25, we get (10 + 10 + 2 + 1 = 23) with remainder 9.
(p) 900 ÷ 15
Ans:  Thus, when 900 is divided by 15, we get (10 + 10 + 10 + 10 + 10)
Thus, when 900 is divided by 15, we get (10 + 10 + 10 + 10 + 10)
(q) 658 ÷ 32
Ans: 
Thus, when 658 is divided by 32, we get (10 + 10 = 20) with remainder 18.
(r) 974 ÷ 9
Ans: 
Thus, when 974 is divided by 9, we get (100 + 5 + 2 + 1 = 108) with remainder 2.
Page No. 201
Chinnu's Coins
Q1: Five friends plan to visit an amusement park nearby. Each of them uses different notes and coins to buy the ticket. The cost of the ticket is ₹750.
- Bujji has brought all notes of ₹ 200.
- And Munna has brought all notes of ₹50.
- Whereas Balu has brought all notes of ₹20.
- And guess what, Chinnu has all coins of ₹5.
- And Sansu has all coins of ₹2.
(a) Find out how many notes/coins each child has to buy the ticket.
Ans: Bujji: ₹750 ÷ ₹200 = 3 notes and ₹150 left → Needs 4 notes (₹800), will get ₹50 back.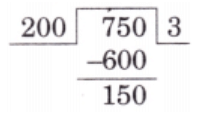
Munna: ₹750 ÷ ₹50 = 15 notes

Balu: ₹750 ÷ ₹20 = 37 notes and ₹10 left → Needs 38 notes (₹760), will get ₹10 back
Chinnu: ₹750 ÷ ₹5 = 150 coins

Sansu: ₹750 ÷ ₹2 = 375 coins

(b) Which of these children will not receive any change from the cashier?
Ans: Munna, Chinnu, and Sansu will not receive any change from the cashier.
(c) How long would the cashier take to count Chinnu's coins?
Ans: 150 coins at ~2 seconds each = 150 × 2 = 300 seconds = 5 minutes.
Q2: Observe the following multiplications. The answers have been provided.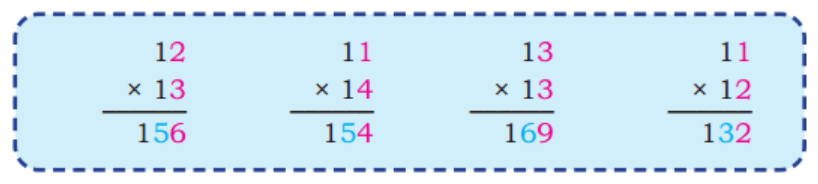 In each case, do you see any pattern in the two numbers and their product? For what other multiplication problems will this pattern hold? Find 5 such examples.
In each case, do you see any pattern in the two numbers and their product? For what other multiplication problems will this pattern hold? Find 5 such examples.
Ans: We observe that, the ones digit of the product is the product of ones digits of the multiplicand and multiplier, and the tens digit of the product is the sum of ones digit of the multiplicand and multiplier.
Other such examples are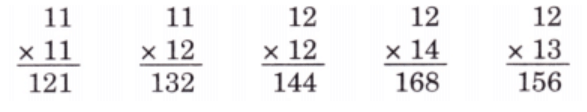
Page No. 202
Q3: Assume each vehicle is travelling with full capacity. How many people can travel in each of these vehicles? Match them up.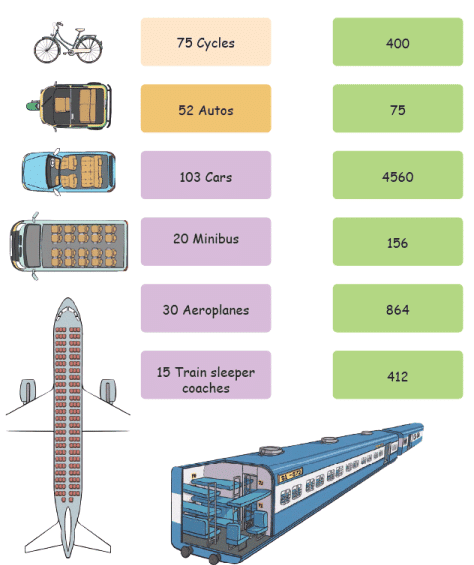 Ans:
Ans: 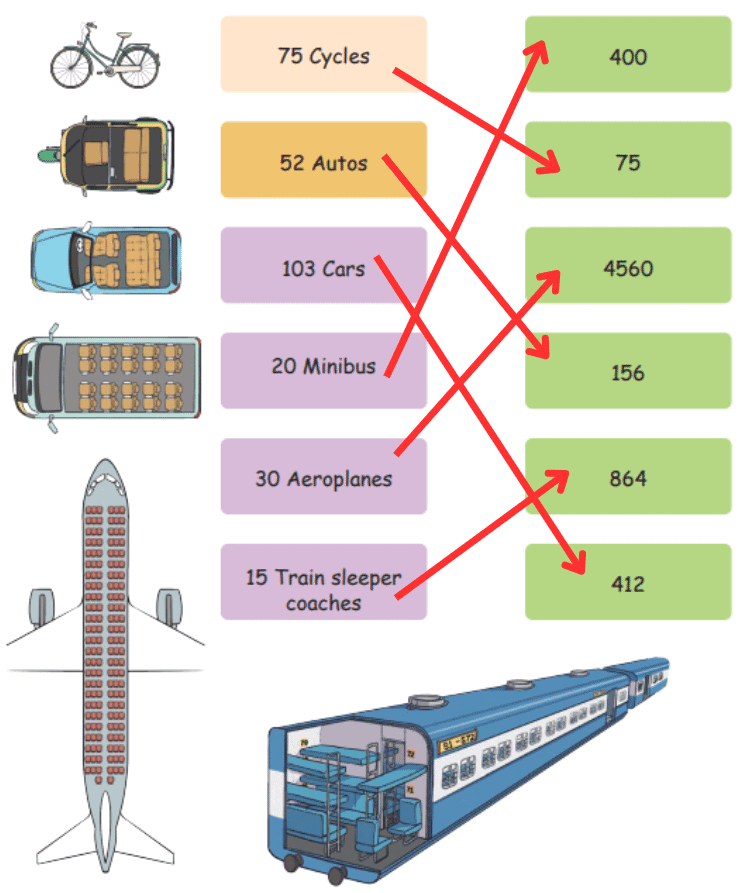
|
54 videos|186 docs|14 tests
|
FAQs on NCERT Solutions for Class 4 Maths Chapter 13 - The Transport Museum
| 1. What types of vehicles can we find in a transport museum? |  |
| 2. Why is it important to visit a transport museum? |  |
| 3. How do transport museums contribute to learning for children? |  |
| 4. Are there any special events held at transport museums? |  |
| 5. How can schools benefit from field trips to transport museums? |  |















