Galilean Transformation | Physics Optional Notes for UPSC PDF Download
| Table of contents |

|
| Introduction |

|
| Galilean Invariance |

|
| Galilean Transformation Equations |

|
| Galilean and Lorentz Transformation |

|
| Limitations of Galilean Transformations |

|
Introduction
In Newtonian mechanics, a Galilean transformation is applied to convert the coordinates of two frames of reference, which vary only by constant relative motion within the constraints of classical physics.
The Galilean group is the collection of motions that apply to Galilean or classical relativity. It is relevant to the four space and time dimensions establishing Galilean geometry.
These transformations make up the Galilean group (inhomogeneous) with spatial rotations and translations in space and time. The homogeneous Galilean group does not include translation in space and time.
In the case of special relativity, inhomogeneous and homogeneous Galilean transformations are substituted by Poincaré transformations and Lorentz transformations, respectively.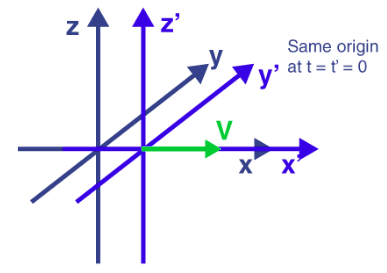
The Galilean transformation equations are only valid in a Newtonian framework and are not at all valid to coordinate systems moving with respect to each other around the speed of light.
Galilean Invariance
Galilean invariance or relativity postulates that the laws governing all fundamental motions are the same in all inertial frames. Galileo derived these postulates using the case of a ship moving at a constant velocity on a calm sea. Any viewer under the deck would not be able to deduce the state of motion in which the ship is at.
Specifically, the term Galilean invariance usually refers to Newtonian mechanics. Under this transformation, Newton’s laws stand true in all frames related to one another.
Consequences of Galilean Relativity
- The basic laws of physics are the same in all reference points, which move in constant velocity with respect to one another.
- All inertial frames share a common time.
Galilean Transformation Equations
These equations explain the connection under the Galilean transformation between the coordinates (x, y, z, t) and (x’, y’, z’, t’) of a single random event. It is calculated in two coordinate systems
S and S’, in constant relative motion (velocity v) in their shared x and x’ directions, with their coordinate origins meeting at time t = t’ = 0.
x’ = x = vt
y’ = y
z’ = z
t’ = t
In the grammar of linear algebra, this transformation is viewed as a shear mapping and is stated with a matrix on a vector. With motion parallel to the x-axis, the transformation works on only two elements.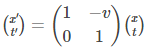
Even though matrix depictions are not strictly essential for Galilean transformation, they lend the ways for direct comparison to transformation methodologies in special relativity.
Galilean and Lorentz Transformation
Galilean and Lorentz transformations are similar in some conditions.
At lesser speeds than the light speed, the Galilean transformation of the wave equation is just a rough calculation of Lorentz transformations. Electromagnetic waves (propagate with the speed of light) work on the basis of Lorentz transformations. It is fundamentally applicable in the realms of special relativity. In contrast, Galilean transformations cannot produce accurate results when objects or systems travel at speeds near the speed of light.
- In the case of two observers, equations of the Lorentz transformation are
- x’ = y(x – vt)
- y’ = y
- z’ = z
- t’ = y(t – vx/c2)
- where, {c = light speed}
- y = 1/(1 – v2/c2)1/2
- As per these transformations, there is no universal time. Time changes according to the speed of the observer. Due to these weird results, effects of time and length vary at different speeds.
- Galilean transformations are estimations of Lorentz transformations for speeds far less than the speed of light.
- Lorentz transformations are applicable for any speed. Galilean transformations are not relevant in the realms of special relativity and quantum mechanics.
- As per Galilean transformation, time is constant or universal. It does not depend on the observer. On the other hand, time is relative in the Lorentz transformation.
Limitations of Galilean Transformations
There are the following cases that could not be decoded by Galilean transformation:
- Galilean Transformation cannot decipher the actual findings of the Michelson-Morley experiment.
- It breaches the rules of the Special theory of relativity.
- In Maxwell’s electromagnetic theory, the speed of light (in vacuum) is constant in all scenarios. But in Galilean transformations, the speed of light is always relative to the motion and reference points. It will be varying in different directions.
FAQs on Galilean Transformation - Physics Optional Notes for UPSC
| 1. What is Galilean Invariance? |  |
| 2. What are Galilean Transformation Equations? |  |
| 3. How do Galilean Transformations differ from Lorentz Transformations? |  |
| 4. What are the limitations of Galilean Transformations? |  |
| 5. Why are Galilean Transformations important in classical mechanics? |  |














