Michelson Interferometer | Physics Optional Notes for UPSC PDF Download
| Table of contents |

|
| Introduction |

|
| Michelson Interferometer |

|
| Determination of λ from circular fringes |

|
| Measurement of Refractive Index of Gas |

|
Introduction
Interferometer is the apparatus to obtain interference fringes with large path difference these fringes can be measured on a scale so the word interferometer. When these interferometer is used to measure refractive index of the substance, it is called a refractometer.
Michelson Interferometer
An interferometer is an instrument in which the phenomenon of interference is used to make precise measurements of wavelengths or distances. In the Michelson interferometer, an incident beam of light strikes a tilted semitransparent mirror and divides the light into a reflected and transmitted wave. These waves continue to their respective mirrors, are reflected, and return to the semitransparent mirror. If the total number of oscillations of the two waves during their separate paths add up to be an integral number just after recombining on the partially reflecting surface of the beam splitter, the light from the two beams will add constructively and be directed toward a detector. This device then acts as a filter that transmits preferentially certain wavelengths and reflects others back to the light source, resulting in a visible interference pattern. A common use of the Michelson interferometer has one mirror mounted upon a carriage so that length of the light path in that branch can be varied. A spectrum is obtained by recording photoelectrically the light intensity of the interference pattern as the carriage is moved when an absorption cell is placed in one of the arms of the interferometer. The resulting signals contain information about many wavelengths simultaneously. A mathematical operation, called a Fourier transform, converts the recorded modulation in the light intensity at the detector into the usual frequency domain of the absorption spectrum. The principal advantage of this method is that the entire spectrum is recorded simultaneously with one detector.
Principle:
In Michelson interferometer, a beam of light from an extended sources is divided into two parts of equal intensities by partial reflection and refraction . These beams travel in two mutually perpendicular directions and come together after reflection from plane mirrors. The beams overlap on each other and produce interference fringes.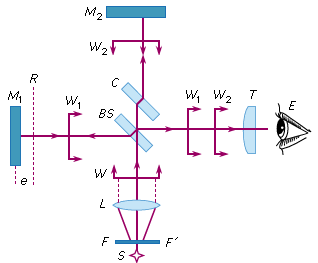
Construction:
Michelson interferometer consists of a beam splitter, a compensating plate, and twp plane mirrors. The beam splitter is a partially silvered plane parallel glass plate. The compensating plate is a simple plane parallel glass plate having the same thickness as beam splitter. The two plates are held parallel to each other and are inclined at an angle of 45° with respect to another mirror. The plane mirrors can be made perfectly perpendicular with the help of the fine screws attached to them. The interference bends are observed in the field of view of telescope T.
Working:
- Beam of monochromatic light is emitted toward a beam splitter.
- The beam splitter separates the incident beam into two separate beams of equal intensity.
- One beam is sent towards a stationary mirror and the other is sent to a movable mirror.
- The incident beams are reflected and sent back towards the beam splitter.
- The beam splitter recombines the waves to produce an interference pattern.
- The interference pattern is projected onto a surface as a series of concentric rings of light and dark.
- As the mirror is moved the successive rings of light and dark change and can be counted (N).

Application:
Michelson interferometer can be used to determine:
- The wavelength of light from a given monochromatic source of light.
- Determination of the difference in the wavelength of two waves.
- Thickness of a thin transparent sheet.
- Determination of the refractive index of gases.
- Standardization of the meter.
Determination of λ from circular fringes
Circular fringes are used to determine the wavelength of the source of light. For a given separation of ‘d’ between the mirrors M1 and M2 and normal incidence (θ=0), the path difference is given as 2d = nλ. If one mirror is moved by a distance Δd and N number of rings appear/disappear at the center, then the path difference after moving the mirror is given as 2(d+ Δd) = (n+N)λ
Hence, λ = 2(Δd)/N
Measurement of Refractive Index of Gas
In one arm of a Michelson interferometer, a glass chamber is placed with attachments for evacuating the inside and putting gases in it. The space inside the container is 2 cm wide. Initially, the container is empty. As gas is slowly let into the chamber, we observe that dark fringes move past a reference line in the field of observation. By the time the chamber is filled to the desired pressure, you have counted 122 fringes move past the reference line. The wavelength of the light used is 632.8 nm. 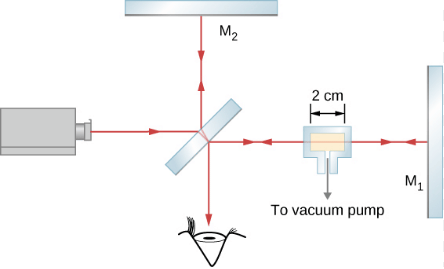
The ray travels a distance t = 2 cm to the right through the glass chamber and another distance t to the left upon reflection. The total travel is L = 2t. When empty, the number of wavelengths that fit in this chamber is
No=L/λo = 2t/λo
where λo=632.8 is the wavelength in vacuum of the light used.
In any other medium, the wavelength is λ = λo/n and the number of wavelengths that fit in the gas-filled chamber is N = L/λ = 2t/(λo/n)
The number of fringes observed in the transition is
m = N − No
= 2t/(λo/n)−2t/λo
= {2t/λo}(n−1)
Solving for (n−1) gives
n−1= m(λo/2t) = 122[(632.8 × 10-9 m)/2(2 × 10-2 m)] = 0.0019
and n = 1.0019
Significance
The indices of refraction for gases are so close to that of vacuum, that we normally consider them equal to 1. The difference between 1 and 1.0019 is so small that measuring it requires a correspondingly sensitive technique such as interferometry. We cannot, for example, hope to measure this value using techniques based simply on Snell’s law.
FAQs on Michelson Interferometer - Physics Optional Notes for UPSC
| 1. What is the principle behind the Michelson Interferometer ? |  |
| 2. How can the wavelength of light be determined using circular fringes in a Michelson Interferometer ? |  |
| 3. What is the method for measuring the refractive index of a gas using a Michelson Interferometer ? |  |
| 4. What are the applications of the Michelson Interferometer in scientific research ? |  |
| 5. Why is coherence important in the functioning of a Michelson Interferometer ? |  |














