Kirchoff's Law | Physics Optional Notes for UPSC PDF Download
Kirchhoff’s First Law or Kirchhoff’s Current Law (KCL)
The first law of Kirchhoff deals with the current in the circuit. According to Kirchhoff’s Current Law, the algebraic sum of currents at any node of a circuit is zero. The total current entering a junction is exactly equal to the total current leaving the junction. This law is based on the Conservation of Charges.
From the below image we can say that: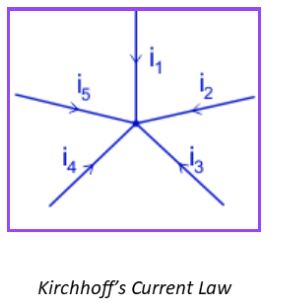
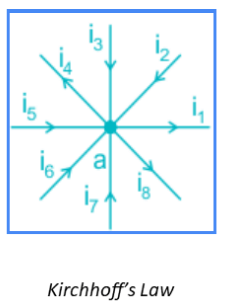
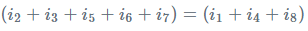
∑ incoming = ∑ outgoing
Q. Find the current in the given circuit.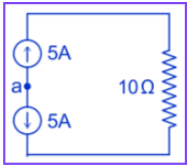
Ans. At a node only one value of current is possible
So, here violation of KCL
So, no current is possible in the circuit.
Memory Tip
KCL applies to any lumped network irrespective of the nature of the network; whether unilateral or bilateral, active or passive, linear or nonlinear.
- KCL does not apply to distributed networks.
- Current always travel in a less resistant path.
- KCL is always giving conservation of charge.
- The maximum amount of current is flowing in a short circuit because of zero resistance.
- There is no flow of current in an open circuit because of infinite resistance.
Kirchhoff’s Second Law or Kirchhoff’s Voltage Law (KVL)
Kirchhoff’s Voltage Law or the second law deals with the voltage drop in a circuit. When current flows in a circuit, the magnitude of the current changes according to the product of current and resistance or emf by which it is connected in the circuit. According to this law, the algebraic sum of voltage (or voltage drops) in any closed path of the network in a specific direction is zero.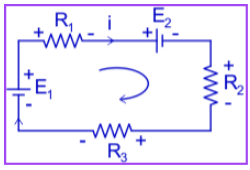
The sign while going moving in the loop totally depends on the user,
If we consider while going from positive (+) to negative (–) (it depends on the user to consider) it acts as a drop or gain.
The answer is unaffected by this sign.
- Suppose we consider it as a drop (-) when going from positive (+) to negative (-).
- Let’s start with Resistance R1. Current goes from one point to another (positive to negative) and the voltage drop is taken as negative (-).
- While moving from EMF E2 current goes from positive to negative and drop is taken as –E2
- Similarly for R2 and R3
- Lastly while moving from E1 current goes from negative to positive and here gain is taken.
-iR1 – E2 – iR2 + E1 = 0
E1 – E2 = iR1 + iR2
Q. Find current I in the given circuit.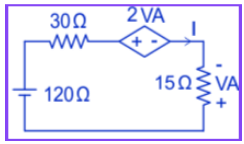
Ans. Apply KVL in the given loop then we get,
120 – 30 I – 2VA + VA = 0
120 = 30 I + VA …………… (1)
Also from Ohm's law at the output, we can get
VA = – 15 I ……………….. (2)
On solving equations (1) and (2) we get
I = 8 Ampere.
So, 8A current is flowing in the circuit.
Memory Tip
- KVL applies to any lumped network irrespective of the nature of the network, whether unilateral or bilateral, active or passive, linear or non-linear.
- KVL does not apply to distributed networks.
- The voltage drop across a short circuit is zero because of zero resistance.
- KVL is always conserving energy.
- A maximum amount of voltage is appeared across the open circuit because of infinite resistance.
- Voltage is constant in a parallel path and is divided into a series path.
Applications of Kirchhoff’s Circuit Law
Kirchhoff’s circuit laws are used to find:
- The values of current, voltage and internal resistance in DC circuits.
- By applying this law we can also find the unknown resistance in the circuit.
- Wheatstone bridge is an important application of Kirchhoff’s law. It is used in mesh and node analysis.
Limitations of Kirchhoff’s Circuit Laws
- The laws of KCL and KVL are not suitable for AC circuits of high frequencies. Current law is applied only when the electric charge in a circuit is constant.
- Where KVL is applied in an assumption that magnetic fields do not change in a closed circuit. So we cannot apply KVL when the magnetic field varies within a circuit.
Circuit Terminology
- Circuit: It is a closed path through which the current flows.
- Path: A path is considered as a single line, which consists of circuit elements and sources.
- Node: A node is defined as a terminal or a junction at which two or more elements will be joined together and thus have a common point for more than one branch.
- Branch: A branch consists of elements like resistors and sources connected between two nodes.
- Loop: A loop is a closed path in which elements are counted just once.
- Mesh: A mesh is an open-loop and open path with no elements in it.
If the elements are connected in series the current which flows through each one is the same. If the elements are connected in parallel the voltage across each component remains the same.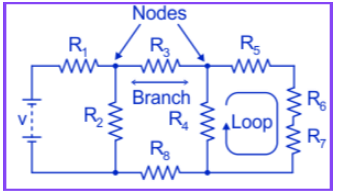
Kirchhoff’s Circuit Laws: Summary
- Gustav Kirchhoff gives a better understanding of solving and application of electrical circuits.
- The first law of Kirchhoff states that the total current that enters a node or junction is equal to the total current or charge leaving the node. It is based on the principle of Conservation of Charge. This is also known as the junction rule.
- The second law of Kirchhoff states that the sum of voltage drops is equal to the sum of voltage rise. This law is based on the Conservation of Energy. This is also known as the loop rule.
Kirchhoff’s Circuit Laws Solved Examples
Example 1: Consider a circuit with three resistors connected in parallel. The currents flowing through the resistors are I1, I2, and I3. The values of the resistors are R1= 3 ohms, R2 = 5 ohms, and R3 = 2 ohms. Find the total current flowing into the circuit.
Sol: Let's assume the currents as follows:
I1 = 2A
I2 = 3A
I3 = 1A
Total current = I1 + I2 + I3
Substituting the given values:
Total current = 2A + 3A + 1A
Total current = 6A
Example 2: Consider a simple series circuit consisting of a 10V battery connected to two resistors R1 and R2. The values of the resistors are R1 = 5 ohms and R2 = 3 ohms. Find the voltage drop across each resistor.
Sol: Let's assume the voltage drops across the resistors as follows:
V1 = Voltage drop across R1
V2 = Voltage drop across R2
Voltage of the battery = Voltage drop across R1 + Voltage drop across R2
10V = V1 + V2
Now, we can apply Ohm's law to find the voltage drops across each resistor:
V1 = I∗R1
V2 = I∗R2
Let's assume the current flowing through the circuit is I.
Substituting the values in the equation:
10V = (I∗R1) + (I∗R2)
10V = I∗(R1 + R2)
10V = I * (5 ohms + 3 ohms)
10V = I * 8 ohms
Now, we can solve for the current:
I = 10V / 8 ohms
I = 1.25A
Substituting the value of current back into the voltage drop equations:
V1 = (1.25A)∗(5ohms)
V1 = 6.25V
V2 = (1.25A)∗(3ohms)
V2 = 3.75V
FAQs on Kirchoff's Law - Physics Optional Notes for UPSC
| 1. What is Kirchhoff’s Current Law (KCL) and how does it apply to electrical circuits? |  |
| 2. What is Kirchhoff’s Voltage Law (KVL) and what does it signify in circuit analysis? | |
| 3. What are the practical applications of Kirchhoff’s Circuit Laws in engineering? | |
| 4. What are some limitations of Kirchhoff’s Circuit Laws that engineers should be aware of? | |
| 5. How do Kirchhoff’s Laws relate to the analysis of parallel and series circuits? | |
Viva Questions
,Previous Year Questions with Solutions
,past year papers
,MCQs
,shortcuts and tricks
,video lectures
,study material
,Semester Notes
,ppt
,Kirchoff's Law | Physics Optional Notes for UPSC
,Exam
,Objective type Questions
,Free
,Kirchoff's Law | Physics Optional Notes for UPSC
,practice quizzes
,Important questions
,Summary
,Extra Questions
,Sample Paper
,Kirchoff's Law | Physics Optional Notes for UPSC
,mock tests for examination
;
Kirchoff's Law Free PDF Download
Importance of Kirchoff's Law
Kirchoff's Law Notes
Kirchoff's Law UPSC Questions
Study Kirchoff's Law on the App
|
© EduRev
|
Education Revolution
|
|
