Rayleigh Jeans Law | Physics Optional Notes for UPSC PDF Download
| Table of contents |

|
| Introduction |

|
| Formula |

|
| Derivation |

|
| Ultraviolet catastrophe |

|
Introduction
The Rayleigh-Jeans Law of radiation gives us the intensity of radiation released by a black body. The law states that the intensity of the radiation emitted by a black body is directly proportional to the temperature and inversely proportional to the wavelength raised to a power of four. However, this law works for only low frequencies. Lord Rayleigh derived the law in 1900. Between 1905 and 1909, J. Jeans conducted some work on standing waves by applying statistical mechanics and arrived at the equation derived by Rayleigh. This law can be considered a special case of Planck’s law for a small frequency. It can also be used in place of Planck’s law when the wavelength is sufficiently long and when high accuracy is not required.
Formula
The Rayleigh-Jeans law approximates the spectral radiance of a black body as a function of its wavelength at a given temperature. The Rayleigh-Jeans equation can be written as: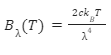
Where, B= spectral radiance, kB= Boltzmann constant c= speed of light T= Temperature in Kelvin For frequency v, the Rayleigh’s equation can be written as: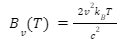
The Rayleigh-Jeans equation for energy density (uν) can be written as: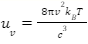
The law can be applied to low frequencies (large wavelengths) but not high frequencies (short wavelengths). This failure of the law was termed as an ultraviolet catastrophe. A better substitute for this law is Planck’s law which gives the correct radiation at low and high frequencies.
Derivation
Let us consider a cube such that radiation is reflected off its surface. Suppose that the cube has an edge of length L and the radiation wavelength is λ. Standing waves occur for a number of half-waves that occupy an area on the cube and whose radiation is of λ wavelength. For radiation that is parallel to the edge,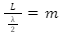
Or,
λ = 2L/m
where m is an integer.
Now, frequency (v) can be written as, v = c/λ, where c denotes the speed of light. Substituting the value of in the equation for frequency, we get,
v = cm ⁄ 2L
Now let us consider a quantity, q (wavenumber). Suppose it is defined as:
q = 2π ⁄ λ
Substituting =c/v in the above equation we get,
q = 2πv ⁄ c
Again, substituting v = cm2L in the above equation, we get,
q = 2πcm ⁄ 2Lc
Or,
q = πm ⁄ L
Squaring both sides,
q² = π²(m/L)²
Now, suppose, mx, my, and mz denote the value of m for the three axes of the cube. Now standing wave will occur when,
On simplifying the above equation, we get,
The aim is to determine the non-negative combinations of mx, my and mz that fit between two spheres of radius R and R+dR respectively.
Now, suppose for the spherical shell, the inner and outer radii are R and R+dR respectively. Its volume will be given by,
dV = 4πR²dR
If,
then, substituting  in the above equation, we get,
in the above equation, we get,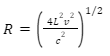
On further simplification, we get,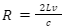
Therefore,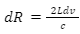
Now, substituting the values of R and dR in the formula for volume, we get,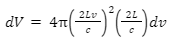
On simplification, we get, 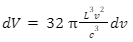
Now, we have to consider the non-negative cases. Since we deal with three dimensions, the non-negative values lie in the first octant. That is, non-negative values constitute 1/8 of the total values. Hence, the number dN is equal to 1/8dV. Therefore,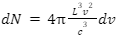
Now, the average energy of radiation per unit frequency can be written as,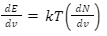
Where,
k = Boltzmann constant
T = absolute temperature
kT = the average of kinetic and potential energy per degree of freedom.
Substituting the value of dN, we get,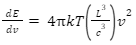
Now, the average density (uv) can be written as,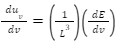
Substituting the value of dE/dv in the above equation, we get,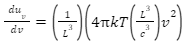
On simplification, we get,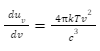
The above formula stands true only for one direction of polarization. If two directions are taken into account, we have to multiply the above equation by 2, therefore,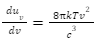
Ultraviolet catastrophe
A conflict or a difference between theory and observation is termed as an ultraviolet catastrophe in physics. The Rayleigh-Jeans law led to an ultraviolet catastrophe. The law predicted that the brightness of black bodies would keep increasing at higher radiation frequencies, and the total power that the body would radiate per unit area would be infinite. This issue was resolved when Max Planck discovered the quantization of energy in the 1900s. This also became the foundation for quantum mechanics.
Conclusion
The Rayleigh-Jeans law was discovered by Lord Rayleigh in the 1900s and later proved by J. Jeans. The law states that the intensity emitted by a black body is directly proportional to the temperature and inversely proportional to the wavelength raised to a power of four. The Rayleigh-Jeans equation for energy density (uv) can be written as: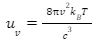
Where, c denotes the speed of light, T denotes temperature, v denotes frequency and kB is the Boltzmann constant.
The law can be applied to low frequencies (large wavelengths) but not high frequencies (short wavelengths). This failure of the law was termed as an ultraviolet catastrophe.
FAQs on Rayleigh Jeans Law - Physics Optional Notes for UPSC
| 1. What is the Rayleigh-Jeans Law and how does it relate to the ultraviolet catastrophe? |  |
| 2. What is the significance of the ultraviolet catastrophe in the context of physics? |  |
| 3. How did Max Planck resolve the issues presented by the Rayleigh-Jeans Law? |  |
| 4. What are the implications of Planck's Law in modern physics? |  |
| 5. How does the Rayleigh-Jeans Law compare to Planck's Law in terms of accuracy? |  |



















