Liquefaction of Gases | Physics Optional Notes for UPSC PDF Download
What is Joule-Thomson Effect?
James Prescott Joule, a British Physicist, and William Thomson, a British physicist, worked together for a long time to coordinate investigations that were intended to dissect the Thermodynamics and propel it. The 1852 disclosure by the experts was particularly remarkable. The specialists discovered that gas can experience temperature changes due to a sudden tension change at a valve. This phenomenon is known as the Joule-Thomson Effect. It is important in the advancement of refrigeration frameworks such as hotness syphons, climate control systems, liquefiers, and climate control systems.
The thermodynamic principle explains the Joule-Kelvin effect best if we consider a separate gas package that is placed in the opposite direction to restrict flow. The upstream gas must perform some work to allow the gas packet through. The work is equal to the volume of the packet divided by the times of pressure.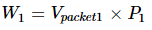
As a packet passes through the restriction, it must make room by displacing some of the downstream gases. This includes the work that equals the sum of the downstream pressure and packet volume.
So,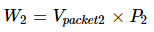
Due to the different effects caused by compressibility, the work done upstream is not the same as the work done downstream for real gases. De-pressuring can be viewed as an adiabatic phenomenon. It reveals that any gas doesn’t exchange heat or work with its surroundings. Any change in internal energy must follow the first law.
Therefore,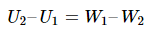
As they move in random order, gas molecules are subject to Van der Waals forces (repulsive and attractive forces). The attractive forces dominate many gases at ambient temperatures when the gas pressure is decreased, which means that the average distance between molecules decreases. This increases potential energy. Due to compressibility, most of the real gases require more work downstream at ambient temperatures.
Now,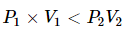
This means that the gas’s internal energy decreases as it passes through the restriction. It is possible to generalise that temperature decreases with a decrease in pressure for most real gases. However, this is not true for all gases. The isenthalpic process of de-pressuring shows that the enthalpy does not change. Based on how the internal energy changes, the temperature of any gas can decrease or increase.
Joule-Thomson Effect Examples
Here are some key examples of the Joule-Thomson effect:
- Liquefaction of gases: The Joule-Thomson effect is used to liquefy gases by slowly allowing them to expand through a valve or porous plug. As the gas expands, it cools below the inversion temperature and liquefies. This is important industrially for producing liquid gases like liquid nitrogen, oxygen, air, etc.
- Cryocoolers: Devices that use the Joule-Thomson effect to provide cooling below 120 K are known as cryocoolers or Joule-Thomson coolers. They are used in applications like infrared detectors, space telescopes, medical equipment, etc.
- Air conditioning: Basic home air conditioners use the Joule-Thomson effect to cool air. Hot, compressed refrigerant enters the outdoor coil where it cools as it expands through an valve into the indoor evaporator coils.
- Natural gas pipelines: As high-pressure natural gas travels through pipelines and expands at reductions stations, it undergoes Joule-Thomson cooling. This can cause some of the gas to condense into liquid if the temperature drops below the inversion point.
Joule-Thomson Coefficient
Joule-Thomson coefficient is the temperature change of the fluid at varying pressure to maintain its enthalpy constant. It can be described as follows: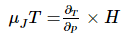
Derivation of Joule-Thomson Coefficient
The Joule-Thomson coefficient will be calculated using laws of Thermodynamics and will be written as:
The first step in getting these results is to recognize that the Joule-Thomson coefficient of Joule-Thomson effect is a combination of three variables: that are T, P and H. The most useful results are achieved through the application of the cyclic rule that is based on the three variables, the rule could be written as: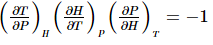
Each of the three partial derivatives in this expression has a specific meaning. The first one is , μJT the second one is the constant pressure heat capacity, CP, defined by: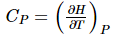
and the third is the inverse of the isothermal Joule–Thomson coefficient, μT, defined by: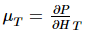
This last quantity is more easily measured than μJT. Thus, the expression from the cyclic rule becomes: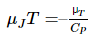
This equation can be used to obtain Joule–Thomson coefficients from the more easily measured isothermal Joule–Thomson coefficient. It is used in the following to obtain a mathematical expression for the Joule–Thomson coefficient in terms of the volumetric properties of a fluid.
To proceed further, the starting point is the fundamental equation of thermodynamics in terms of enthalpy; this is
Now dividing through by dP, while holding temperature constant, yields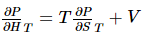
The partial derivative on the left is the isothermal Joule–Thomson coefficient μT, and the one on the right can be expressed in terms of the coefficient of thermal expansion via a Maxwell relation. The appropriate relation is,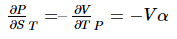
where α is the cubic coefficient of thermal expansion. Replacing these two partial derivatives yields
This expression can now replace μT in the earlier equation for μJT to obtain: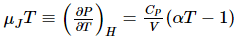
This gives an expression for the Joule-Thomson coefficient in terms of the widely available properties of heat capacity and molar volume and the thermal expansion coefficient. It demonstrates that the Joule-Thomson inversion temperature, where it is zero, is at the point where the thermal expansion coefficient is the same as the reverse of temperature. This is the case regardless of temperature for perfect gases the Joule-Thomson coefficient of an ideal gas will be zero at all temperatures.
Applications of Joule-Thomson Effect
The applications of the Joule-Thomson effect are mentioned as follows:
- It has been a valuable tool in refrigeration because of the cooling it produces in the Joule-Thomson expansion.
- This cooling effect is used in the Linde technique, which is used in the petrochemical sector to liquefy gaseous substances.
- It can also be used in cryogenic applications. It is used, for example, to produce liquid nitrogen, oxygen, and argon.
- This effect can also be used for liquefying helium.
Liquefaction of Gases
Whatever has to be transformed from a gaseous state to a liquid state must be liquefied first. Temperature, pressure, and volume are only a few of the physical factors contributing to this transformation. Thomas Andrew was the one who discovered that Carbon Dioxide could change the state from a gas to a liquid state. Since then, it has been shown that most true gases behave similarly to carbon dioxide, turning from a gas to a liquid at the proper temperature and pressure.
Because of his experiments with CO2, Andrews concluded that gases could not be liquefied even at very high temperatures and pressure levels. Additionally, the gases diverge dramatically from their optimal behavior. Carbon dioxide started to convert into a liquid at 30.98𝆩 Celsius.
Limits for Pressure, Volume, and Temperature
The results of Andrews’ experiment revealed that, regardless of how high the pressure was applied, the gas sample could not be liquefied above a specific temperature. Gases can only become liquids when their critical temperature is lowered below a certain point. The pressure required to liquefy a gas increases in direct proportion to the temperature of the gas. Temperatures far higher than this one were the only ones that resulted in gas turning to a liquid state. It’s referred to as the critical temperature point or Tc.
The crucial constants are the variables that determine the state of matter. The most critical constants are pressure, temperature, and volume. If one mole of a gas volume liquefies at the critical temperature, it is called Vc or Pc. When the required volume (Vc) and necessary pressure (Pc) are reached, the mole and pressure are referred to as Vc and Pc.
The Method of Liquefaction of Carbon Dioxide
It is vital to monitor changes in both volume and pressure. The methods of liquefaction of gases of carbon dioxide in the isotherm.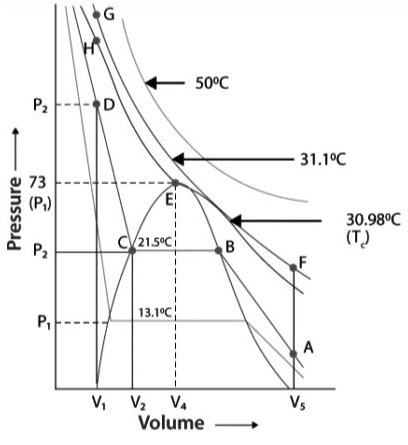
Andrews who performed a series of experiments on the pressure-volume relationship of carbon dioxide under varied conditions of temperature. Names for these curves include P–V isotherms of CO2. The isotherm was found at 0°C, 21.1°C, 31.1°C, and 50°C.
- Point A, the lowest temperature selected, i.e. 13.1°C at low pressure, is where carbon dioxide appears as a gas.
- As can be seen, the volume of the gas decreases as the pressure rises along the curve.
- When carbon dioxide hits 21.5°C, it acts as a gas until point B.
- When it comes to point B, the gas has a dual state: it is both liquid and gas.
- To put it another way, at point C all of the carbon dioxide condenses, leading to a rise in pressure.
- When liquefaction occurs, the volume of the gas quickly reduces due to the liquid’s lower volume than the gas’s.
- Once the liquefaction process is complete, the increase in pressure has very little effect on the volume of the liquid. In the end, this produces a sharp curve. Slope demonstrates that the liquid isotherm is present.
- Below 30.98°C, the gas behaves quite differently under compression, and each curve exhibits a distinct pattern. Just the horizontal line length grows at lower temperatures, and at the critical point, the horizontal component of the isotherm merges into one point.
- As long as pressure is maintained above 30.98°C, the gas will not condense. As a consequence, 30.98°Cis determined to be the threshold temperature for CO2.
- It was observed that all gases behave similarly to carbon dioxide because of the isothermal compression.
- The critical temperature is vital in the liquefaction of gases. Liquefaction is possible only if the gas temperature falls below a certain threshold. NH3, CO2, SO2, and other gases with a high critical temperature may be liquefied by increasing the pressure.
We observe that, as a result of the constant temperature or isothermal compression, all gases behave like CO2. Isothermal compression is a word used to describe the identical behavior of gases when compressed at a constant temperature, regardless of the temperature. It is impossible to liquefy H2, He, and other low-critical-temperature gases by applying pressure alone. To liquefy, they must be refrigerated to a temperature below their critical point and then subjected to the right amount of pressure.
Liquidification of Gases Requires Specific Environmental Conditions
Gas cooling may be done using the following principles:
- By reducing the gas’s temperature below the critical point.During an adiabatic transition from a high-pressure zone to a low-pressure zone, the temperature of the gas drops below its inversion temperature. This phenomenon is known as the Joule–Thomson effect. The Joule-Thomson effect is a well-known phenomena used in the liquefaction of gases.
- A gas loses part of its kinetic energy as it expands adiabatically via mechanical effort, and the temperature decreases.
Conditions
- The critical temperature of a gas is when liquefaction starts to occur in a certain amount of time.
- The strength of intermolecular forces of attraction increases as the critical temperature rises, making gas liquefaction more straightforward at higher temperatures.
Methods of Air Liquefaction
- Linde’s method of liquefaction of gases: Linde’s method of liquefaction of gases which repeatedly compresses, cools, and expands air to reduce its temperature, is used as a Method of Air Liquefaction. Soluble air may be formed as the air temperature drops since the molecules move more slowly and take up less space.
- Claude’s method: When air is heated and allowed to expand isentropically twice in two chambers, it may also be liquefied. As it passes through an expansion turbine, the gas is forced to exert energy throughout its expansion. The turbine would be destroyed if the gas became liquid. By expanding the air to supercritical pressures, commercial air liquefaction facilities avoid this issue. Thermal expansion valves are used to complete the final liquefaction process.
Methods of liquefaction of gases Require Cooling and Compression
Does a gas liquefies need both cooling and compression to achieve this liquefaction? To change the state of gases that have a positive deviation from the compressibility factor (Z), it is essential to cool and compress them simultaneously.
As for Explanation:
With a Freezing combination, it is not possible to drop the temperature of a gas very much. Ammonia, for example, has a critical temperature of 406K (271.4°F [133°C].). Because this temperature is just over the freezing point of water, converting ammonia gas to a liquid is a simple matter of applying sufficient pressure. This means that for most gases, such NH3 and CO2, the process temperature may be reduced to as low as -20°C using a salt and ice combination. For the other gases, however, the process temperature can be reduced to as low as -54°C by mixing calcium chloride with ice and Ether. Even though the colder the gas is to begin with, the less pressure is necessary to compress it, the pressure at its critical temperature is 112.5 atmospheres.
Changes in Temperature as a Result of Compression and Heating
As a consequence of compression, the pressure of gas molecules rises as the molecules squeeze together. This procedure has the effect of bringing molecules closer together. A decrease in random mobility occurs as soon as the molecules come into touch with one another, caused by the reduced temperature in their surroundings. This is due to the combined impact of compression and cooling, which causes intermolecular connections to be activated. Because of this intermolecular contact, the molecules move closer to one another, causing changes in their physical states.
Conclusion
Liquidizing a gas necessitates the gathering of its constituent components in one place. This may be accomplished by lowering the temperature while increasing the pressure in the system. When a gas is subjected to a specific amount of pressure, the molecules must grow closer together for the gas to become a liquid.
Despite this, when the temperature of a gas is reduced, the molecules lose kinetic energy, resulting in a significant fall in the velocity of the gas. A liquid is formed due to the attraction between molecules that are too slow to resist the force of the attraction.
Gas liquefaction is caused by a combination of low temperature and high pressure.
FAQs on Liquefaction of Gases - Physics Optional Notes for UPSC
| 1. What is the Joule-Thomson Effect and how does it occur? |  |
| 2. Can you provide examples of the Joule-Thomson Effect in everyday applications? |  |
| 3. What is the Joule-Thomson coefficient and how is it significant? |  |
| 4. What are the key applications of the Joule-Thomson Effect in modern technology? |  |
| 5. How is carbon dioxide liquefied using the Joule-Thomson Effect? |  |















