Chandrasekhar Limit | Physics Optional Notes for UPSC PDF Download
| Table of contents |

|
| Introduction |

|
| Chandrasekhar Limit Derivation |

|
| Significance of Chandrasekhar Limit |

|
| Application of Chandrasekhar Limit |

|
| Facts on Chandrasekhar Limit |

|
Introduction
In astrophysics, the Chandrasekhar limit is the maximum mass theoretically possible for a stable white dwarf star. This limiting value was named after Subrahmanyam Chandrasekhar, an Indian-born astrophysicist who developed it in 1930.
Using Albert Einstein’s Special Theory of Relativity and quantum physics principles, Chandrasekhar demonstrated that a white dwarf star supported solely by a degenerate gas of electrons could not be stable if its mass exceeds 1.44 times that of the Sun.
The limiting mass may be slightly larger if a star does not completely deplete its thermonuclear fuel. All direct masses determined for actual white dwarf stars have been less than the Chandrasekhar limit.
Chandrasekhar Limit Derivation
The Chandrasekhar limit is expressed in terms of Planck mass and proton mass. The upper limit is about 1.44 times the mass of the Sun. White dwarfs with masses greater than the limit cannot balance gravitational collapse through relativistic electron degeneracy.
Based on the equation of state, the Chandrasekhar limit has provided the following expression for an ideal Fermi gas. The Chandrasekhar limit equation is as follows: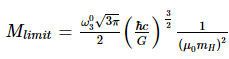
Where
ħ refers to the Planck constant in its reduced form.
The letter c stands for the speed of light.
G stands for the gravitational constant.
The average molecular weight per electron, denoted by μe, is solely determined by the chemical composition of the star.
The mass of a hydrogen atom is denoted by mH.
A constant link with a solution to the Lane-Emden equation is denoted by 3 ≈ 2.018236.
A simplified Chandrasekhar limit derivation begins by defining total energy as the kinetic energy of the degenerate Fermi electron gas plus gravitational potential energy.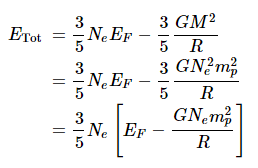
The degenerate Fermi gas’s kinetic energy has a relativistic expression.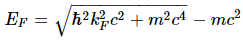
where the Fermi k-vector can be expressed as a function of the white dwarf’s radius and total number of electrons, as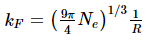
If the star is made entirely of hydrogen, its mass is expressed in terms of the total number of electrons and the mass of the proton.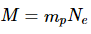
By taking its derivative with respect to the star’s radius, the total energy of the white dwarf is minimised.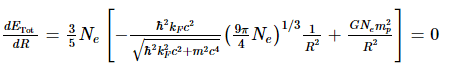
When the derivative is set to zero, the term in brackets is transformed into
The radius for which the electron degeneracy pressure stabilises the gravitational pressure is solved.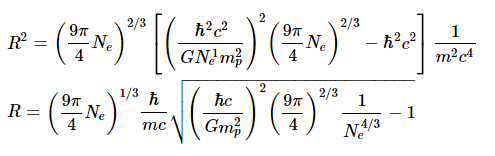
The relativistic radius-mass expression for the size of the stabilised white dwarf as a function of mass is given here (or total number of electrons). One of the most astounding outcomes of this calculation is the combination of astronomically large numbers (the masses of stars) with both relativity and quantum physics. The radius of the white dwarf is actually expressed as a multiple of the electron’s Compton wavelength.
The square root expression shrinks as the size of the star grows larger, and there is an upper limit to the mass of the star beyond which the square root argument becomes negative. The Chandrasekhar limit is defined when the argument equals zero.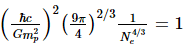
This yields the final Chandrasekhar limit expression (expressed in terms of the Planck mass)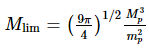
Significance of Chandrasekhar Limit
The Chandrasekhar limit is significant because it is accepted to be 1.44 times the mass of the sun. This means that if a white dwarf is within it, it will remain that way indefinitely. In contrast, a star that exceeds the limit will explode, transforming into a supernova.
The significance of the Chandrasekhar limit lies in its ability to explain the properties of white dwarfs and their ultimate fate. It also plays a crucial role in our understanding of the life cycle of stars and the evolution of galaxies. Additionally, it is also used in the confirmation of the existence of Neutron Stars and Black Holes.
Application of Chandrasekhar Limit
The Chandrasekhar limit has the following applications:
- When the nuclei of lighter elements fuse with those of heavier elements, the heat released prevents the star’s core from collapsing.
- When a star collapses due to nuclei exhaustion, the core of the star condenses.
- Because gaining energy through fusion is impossible with iron ions, a dangerous situation occurs when iron accumulates in the core.
- If the star has less than 8 solar masses, it will eventually reach a mass level lower than the Chandrasekhar limit.
- Stars with more mass will be converted into black holes because the pressure caused by electron degeneration will keep them from collapsing until the density reaches an extreme.
- The neutrinos absorb the energy created by the decreasing potential energy, which is approximately 1046 joules.
Facts on Chandrasekhar Limit
- The Chandrasekhar limit is approximately 1.44 times the mass of the sun.
- It is the upper limit of mass that a white dwarf star can have before collapsing under its own gravity.
- The collapse of a white dwarf star above the Chandrasekhar limit can lead to a supernova explosion or the formation of a neutron star or black hole.
- The limit was first calculated by Indian astrophysicist Subrahmanyan Chandrasekhar in 1930.
- It is supported by quantum mechanics and special relativity theory.
- It is an important concept in the field of astrophysics, providing insight into the properties of white dwarfs and the end stages of stellar evolution.
- The discovery of the limit helped Chandrasekhar win the 1983 Nobel Prize in Physics.
- It is used in the confirmation of the existence of Neutron Stars and Black Holes.
- The neutron stars are formed when the mass of the white dwarf exceeds the Chandrasekhar limit and its gravity becomes so intense that electrons are forced to combine with protons, forming neutrons.
- The limit is dependent on the chemical composition of the white dwarf.
FAQs on Chandrasekhar Limit - Physics Optional Notes for UPSC
| 1. What is the Chandrasekhar Limit and who formulated it? |  |
| 2. Why is the Chandrasekhar Limit significant in astrophysics? |  |
| 3. How does the Chandrasekhar Limit affect the lifecycle of a star? |  |
| 4. What are some applications of the Chandrasekhar Limit in modern astrophysics? |  |
| 5. Can you provide some interesting facts about the Chandrasekhar Limit? |  |














