Numbers Chapter Notes | Mathematics Class 3 ICSE PDF Download
Introduction
Numbers are like the building blocks of math! We use numbers to count things, like how many toys you have or how many friends are playing with you. Numbers help us understand quantities and put things in order. In this chapter, we’ll learn about big numbers (up to thousands), how to write them, compare them, and even round them off to make them easier to use.

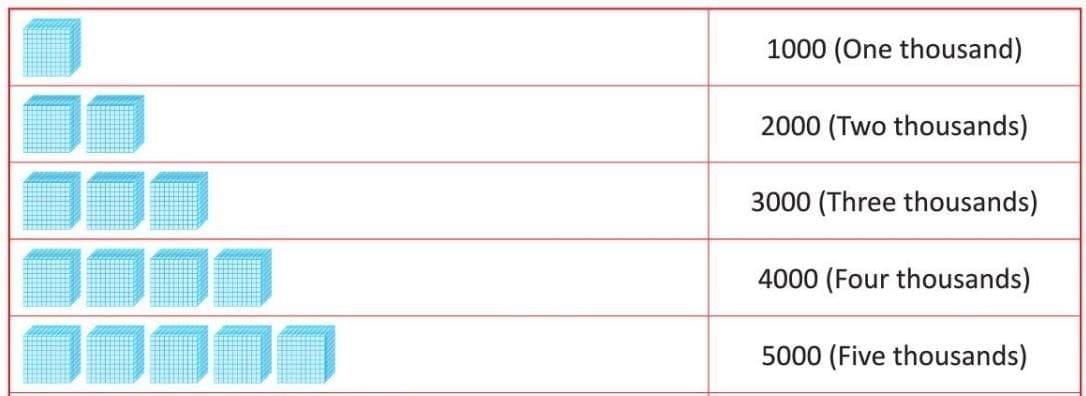
Counting by Thousands
When we count small things, like 1, 2, 3, we use single numbers. But when things get bigger, like counting stars or candies, we need bigger numbers! After 999, we start counting by thousands.
For example:
- 1000 is one thousand.
- 1001 is one thousand and one.
- 2000 is two thousand.
Example: A school has 2456 students. This number is read as "two thousand four hundred fifty-six." It’s made up of 2 thousands, 4 hundreds, 5 tens, and 6 ones.
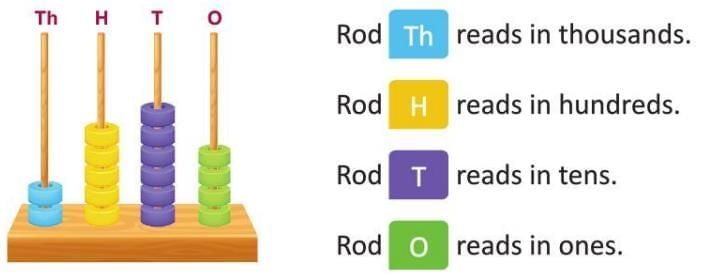
Numbers and Number Names
Every number has a name, just like you have a name! We write numbers using digits (0, 1, 2, 3, 4, 5, 6, 7, 8, 9), but we can also write them as words called number names.
For example:
- The number 25 is written as "twenty-five."
- The number 100 is "one hundred."
- The number 1234 is "one thousand two hundred thirty-four."
Example: Let’s write the number name for 2564.
On abacus 2564 is shown as,
- 2 is in the thousands place, so it’s "two thousand."
- 5 is in the hundreds place, so it’s "five hundred."
- 6 is in the tens place, so it’s "six."
- 4 is in the ones place, so it’s "four."
- Together, 2564 is "two thousand five hundred sixty-four."
Place Value and Face Value
Every digit in a number has a special job based on its position, called its place value. The same digit can mean different things depending on where it sits in a number. The face value is just the digit itself, no matter where it is.
Place Value: In the number 3456:
- 3 is in the thousands place, so its place value is 3 × 1000 = 3000.
- 4 is in the hundreds place, so its place value is 4 × 100 = 400.
- 5 is in the tens place, so its place value is 5 × 10 = 50.
- 6 is in the ones place, so its place value is 6 × 1 = 6.
Face Value: The face value of 3 in 3456 is just 3, because that’s the digit itself.
Example: In the number 7281:
- The place value of 7 is 7 × 1000 = 7000 (thousands).
- The place value of 2 is 2 × 100 = 200 (hundreds).
- The place value of 8 is 8 × 10 = 80 (tens).
- The place value of 1 is 1 × 1 = 1 (ones).
- The face value of 7 is 7, of 2 is 2, of 8 is 8, and of 1 is 1.
Expanded Form and Standard (Short) Form
- Expanded Form: This is like stretching a number to show what each digit is worth based on its place.
- For example, the number 4567 can be written as:
- 4567 = 4000 + 500 + 60 + 7
- Here, 4 is 4000 (thousands), 5 is 500 (hundreds), 6 is 60 (tens), and 7 is 7 (ones).
- Standard (Short) Form: This is the usual way we write numbers, like 4567.
Example: Let’s write 3924 in expanded form:
- 3 is in the thousands place: 3 × 1000 = 3000.
- 9 is in the hundreds place: 9 × 100 = 900.
- 2 is in the tens place: 2 × 10 = 20.
- 4 is in the ones place: 4 × 1 = 4.
- So, 3924 = 3000 + 900 + 20 + 4.
- The standard form is just 3924.
Comparison of Numbers
Comparing numbers means finding out which number is bigger or smaller. To compare numbers, we look at their digits step by step:
- First, check if the numbers have the same number of digits. If not, the number with more digits is bigger.
- If they have the same number of digits, compare the digits from left to right:
- Start with the thousands place. If one number has a bigger digit, it’s the larger number.
- If the thousands are the same, move to the hundreds, then tens, then ones.
Example: Compare 3456 and 3498:
- Both have 4 digits, so compare step by step:
- Thousands: 3 (in 3456) and 3 (in 3498) are the same.
- Hundreds: 4 (in 3456) and 4 (in 3498) are the same.
- Tens: 5 (in 3456) and 9 (in 3498). Since 5 < 9, we stop here.
- So, 3456 < 3498.
Example: Compare 5678 and 4321:
- Both have 4 digits.
- Thousands: 5 (in 5678) and 4 (in 4321). Since 5 > 4, we stop here.
- So, 5678 > 4321.
Ascending and Descending Order
- Ascending Order: Arranging numbers from smallest to largest, like climbing up a ladder.
- Descending Order: Arranging numbers from largest to smallest, like sliding down a slide.
Example 1: Arrange 2345, 1234, 3456, 2346 in ascending order:
- Compare the numbers: 1234 is the smallest, then 2345, 2346, and 3456 is the largest.
- Ascending order: 1234, 2345, 2346, 3456.
Example 2: Arrange the same numbers in descending order:
- Descending order: 3456, 2346, 2345, 1234.
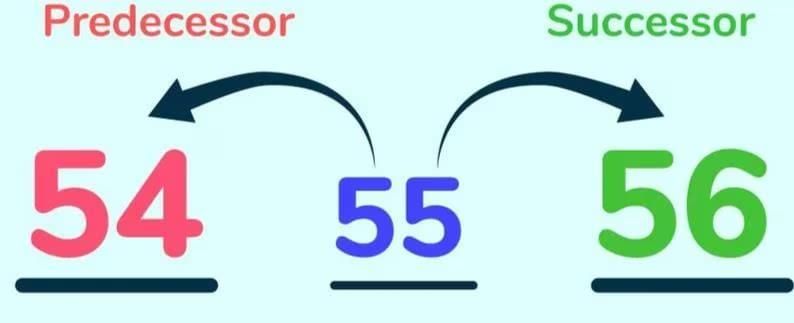
Before, After, and Between
Consecutive numbers are numbers that come one after another in order.
- Example: 1, 2, 3, 4, 5 – these are consecutive numbers because each number is one more than the one before.
- Think of it like steps: when you climb stairs, you take one step at a time — just like consecutive numbers.A
A predecessor is the number that comes just before another number.
- Example: The predecessor of 6 is 5, because 5 comes right before 6.
- Trick to remember: “Pre-” means before.
A successor is the number that comes just after another number.
- Example: The successor of 6 is 7, because 7 comes right after 6.
- Trick to remember: “Succeed” means to come after.
- Before: The number that comes just before another number (one less). For example, the number before 100 is 99.
- After: The number that comes just after another number (one more). For example, the number after 100 is 101.
- Between: The number that comes between two numbers. For example, 100 is between 99 and 101.
Forming 4-Digit Numbers (With or Without Repeating Digits)
A 4-digit number has four places: thousands, hundreds, tens, and ones. We can use digits (0 to 9) to form these numbers. The thousands place cannot be 0, or it won’t be a 4-digit number.
- With Repeating Digits: Digits can be used more than once, like 1122 (1 is repeated, 2 is repeated).
- Without Repeating Digits: Each digit is used only once, like 1234 (all digits are different).
Example: Using digits 2, 3, 5, 7:
- With repeating digits: 2233, 5555, 7272 are all possible.
- Without repeating digits: 2357, 3725, 7523 are possible (each digit used once).
Example: Form the smallest 4-digit number using 1, 4, 6, 8 without repeating:
- Arrange digits in ascending order: 1, 4, 6, 8.
- Smallest number: 1468.
- Form the largest: Arrange in descending order: 8, 6, 4, 1 → 8641.
Rounding Off Numbers

Rounding off makes numbers simpler by changing them to the nearest 10, 100, or 1000.
- It’s like guessing the closest easy number.
Rounding Off to the Nearest 10
- Look at the ones digit.
- If the ones digit is 5 or more, round up (add 1 to the tens digit).
- If the ones digit is less than 5, round down (keep the tens digit the same).
Example 1: Round 47 to the nearest 10.
- Ones digit is 7 (7 ≥ 5), so round up.
- 47 becomes 50.
Example 2: Round 42 to the nearest 10.
- Ones digit is 2 (2 < 5), so round down.
- 42 becomes 40.
Rounding Off to the Nearest 100
- Look at the tens digit.
- If the tens digit is 5 or more, round up (add 1 to the hundreds digit).
- If the tens digit is less than 5, round down (keep the hundreds digit the same).
Example 1: Round 456 to the nearest 100.
- Ten's digit is 5 (5 ≥ 5), so round up.
- 456 becomes 500.
Example 2: Round 432 to the nearest 100.
- The tens digit is 3 (3 < 5), so round down.
- 432 becomes 400.
Rounding Off to the Nearest 1000
- Look at the hundreds digit.
- If the hundreds digit is 5 or more, round up (add 1 to the thousands digit).
- If the hundreds digit is less than 5, round down (keep the thousands digit the same).
Example 1: Round 3456 to the nearest 1000.
- The hundreds digit is 4 (4 < 5), so round down.
- 3456 becomes 3000.
Example 2: Round 3789 to the nearest 1000.
- The hundreds digit is 7 (7 ≥ 5), so round up.
- 3789 becomes 4000.
Practice Questions
- Write the number name for 7894.
- What is the place value and face value of 6 in the number 4623?
- Write 5821 in expanded form and standard form.
- Arrange these numbers in descending order: 4567, 1234, 7890, 2345.
- Round off 6723 to the nearest 10, 100, and 1000.
|
67 docs|9 tests
|
FAQs on Numbers Chapter Notes - Mathematics Class 3 ICSE
| 1. What is the difference between face value and place value? |  |
| 2. How do you write a number in expanded form? |  |
| 3. What does it mean to round off a number? |  |
| 4. How can I compare two numbers to determine which is larger? |  |
| 5. What are ascending and descending order in terms of numbers? |  |