Multiplication and Division Chapter Notes | Year 3 Mathematics IGCSE (Cambridge) - Class 3 PDF Download
| Table of contents |

|
| Introduction |

|
| Exploring multiplication and division |

|
| Connecting 2×, 4× and 8× |

|
| Connecting 3×, 6× and 9× |

|
Introduction
This chapter helps us to understand multiplication and division in detail. We learn about multiples, fact families, and the patterns in times tables. We also connect different multiplication tables like 2, 4, 8 and 3, 6, 9. Using multiplication and division together makes it easier to solve real-life problems involving groups, sharing, arrays, and repeated addition.
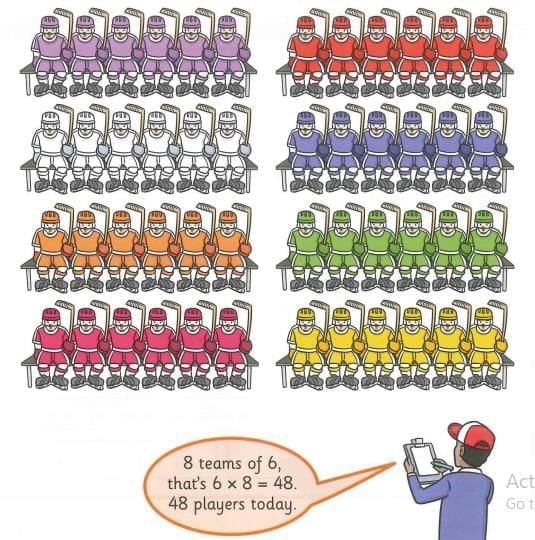
Exploring multiplication and division
- Recognise multiples of 2, 5 and 10.
- Understand that multiples of 2 are always even numbers.
- Sort numbers into groups such as multiples of 5, multiples of 10, or both, using a Venn diagram.
- Notice that multiples of 10 always belong in both groups (overlap in diagram).
- Understand why multiples of 10 are special numbers.
- Create multiplication and division fact families (e.g. 3 × 10 = 30, 10 × 3 = 30, 30 ÷ 3 = 10, 30 ÷ 10 = 3).
- Check and correct mistakes in fact families.
- Learn that multiplication is commutative (3 × 10 = 10 × 3).
- Multiply single-digit and 2-digit numbers by 10 using place value (digits move one place left).
- Recognise that the answer becomes larger and usually ends in zero.
- Use arrays and diagrams to explain multiplication and division facts.
- Solve real-life problems like finding how many pencils in 23 boxes of 10 pencils.
Discuss how finding a fact family in multiplication is similar to finding a fact family in addition. Notice differences between multiplication/division fact families and addition/subtraction ones.
I can recognise multiples of 2, 5 and 10. - I can make multiplication and division fact families from known tables.
- I can multiply single-digit and 2-digit numbers by 10.
Connecting 2×, 4× and 8×
Learn multiplication tables for 4 and 8 by linking them to the 2 times table.
Understand that:
- Multiples of 2 are even numbers.
- Multiples of 4 and 8 are also even numbers because they come from doubling 2.
Use doubling and halving to connect the tables:
- Double the 2× facts to get the 4× facts.
- Double the 4× facts to get the 8× facts.
- Halve to move backwards (e.g. from 8× to 4×, or 4× to 2×).
- Identify patterns when counting in 4s or 8s.
- Practise writing sequences with given rules (e.g. add 4 each time).
- Use diagrams like spiders with 8 legs to find multiples of 8.
- Solve problems like finding missing multiplication facts using doubling and halving.
Investigate number patterns using sequences. Check Zara’s conjecture: if the rule is even and the start number is even, all terms will be even. Discuss with a partner to confirm if this is always true.
- I can build and use the multiplication tables for 4 and 8.
- I can connect 2, 4 and 8 times tables by doubling or halving.
- I can count in fours or eights from any number.
Connecting 3×, 6× and 9×
Learn the multiplication tables for 3, 6 and 9.
Connect the tables:
- 6× facts come from doubling 3× facts.
- 9× facts can be found by adding or subtracting multiples of 3.
- Count in 3s, 6s and 9s from any starting number.
- Use counting sticks and sequences to practise multiples.
- Notice patterns in the numbers and describe them using “odd” and “even”.
Find multiplication facts from different tables that give the same result (e.g. 3 × 2 = 6 × 1).
|
65 docs|19 tests
|
FAQs on Multiplication and Division Chapter Notes - Year 3 Mathematics IGCSE (Cambridge) - Class 3
| 1. What is the relationship between multiplication and division? |  |
| 2. How do you connect the concepts of 2×, 4×, and 8× in multiplication? |  |
| 3. What patterns can be seen when multiplying by 3, 6, and 9? |  |
| 4. Why is it important to learn multiplication and division in early education? |  |
| 5. How can visual aids enhance the understanding of multiplication and division? |  |














