Gaseous State
1. Introduction
A given substance may occur in solid, liquid or gaseous phase depending upon the relative value of two tendencies namely mutual attraction (MA) and escaping tendency (ET)
(i) if MA is greater than ET then substance will occur in solid state
(ii) if MA is slightly greater than ET then substance will occur in liquid state
(iii) if MA is very much less than ET then substance will occur in gaseous state
Out of the three states of matter, the most simplest one is the gaseous state.
The state is characterized by sensitivity of volume change with change of pressure and temperature. It is due to large distance between molecules as compared to their own dimensions. There exist weak Vander Waal's forces, molecules move independent of each other with speed about 400 ms-1.
Gases show maximum equality in their behavior irrespective of their nature.
2. Measurable properties of gases
1. Mass
Def. The gases do possess mass. The mass of gas is generally used in the form of number of moles which is related as
(i) no. of moles =
Two other useful formulae to calculate number of moles of gas are -
(ii) number of moles =
(iii) no. of moles =
When container contains more than one gas then molecular mass of mixture is termed as effective molecular mass (EMM) which is intermediate between molecular masses of all the gases present in the container.
Effective molecular mass =
2. volume
Def. Volume of gas is nothing but volume of the container in which it is present.
Relation between different units of volume
1 m3 = 103 dm3 = 103 litre =106 cm3 = 106 ml = 109 mm3.
3. Temperature
Def. Degree of hotness or coldness of a body is measured by temperature
=
=
C - Celcius scale, K - Kelvin scale, F - Fahrenheit scale
Note : In all the problems of gaseous state (i.e. in all gas law equations), temperature must be expressed in kelvin scale. i.e. , t °C + 273 = TK
4. pressure
Def. Force acting per unit area
P =
units :
CGS : dyne/cm2
MKS : Newton/m2 (1N/m2 = 1Pa)
Relation : 1 N/m2 = 10 dyne/cm2
units of pressure :
1 atm = 76 cm of Hg
= 760 mm of Hg
= 760 torr
= 1.01325×105 N/m2
= 101.325 kPa
= 1.01325 bar
= 14.7 lb/In2 (Psi)
= 10.33 meters of H2O
5. Density
Def. mass per unit volume
d =
units :
CGS : g/cm3
mks : kg/m3
Relation : 1 kg/m3 = 10-3 g/cm3
Density of gases
Absolute density Relative density
(mass per unit volume) (Relative to hydrogen turned as vapour density)
(i) d = (i) VD =
(ii) unit : g/l (ii) No unit
(iii) function of temp., pressure, no. of moles (iii) independent of Pressure , Temperature
Note : mass , volume and no. of moles are extensive properties that depend on mass hence then all divertly additive in nature.
Note : density , pressure and Temperature are intensive properties they does not depend on mass hence they are non-additive in nature.
3. The Gas Laws
(i) Boyle's Law :
It relates the volume and the pressure of a given mass of a gas at constant temperature.
Boyle's law states that , "at constant temperature, the volume of a sample of a gas varies inversely with the pressure".
P ≈
(when temperature and number of moles are kept constant)
The proportionality can be changed into an equality by introducing a constant k, i.e.,
P = or PV = k
Boyle's law can be verified by any one of the following three ways graphically.
Alternatively, Boyle's law can also be stated as follows :
"Temperature remaining constant , the product of pressure and volume of a given mass of a gas is constant".
The value of the constant depends upon the amount of a gas and the temperature.
Mathematically, it can be written as,
P1V1 = P2V2 = P3V3 = ..............
Location of straight line and curve changes with temperature in the isotherm shown in the following figure.
According to Boyle's law, PV = Constant at constant temperature
log P + log V = constant
log P = -log V = constant
Illustration 1: A gas is present at a pressure of 2 atm. What should be the increase in pressure so that the volume of the gas can be decreased to 1/4th of the initial value if the temperature is maintained constant.
Solution : PV = constant for a given mass of gas at constant pressure
⇒ P1V1 = P2V2 P1 = 2atm V1 = V V2 = V/4 P2 =?
Now, Þ P2 = 8 atm
Pressure should be increased from 2 to 8 atm
total increase = 8 - 2 = 6 atm.
Illustration 2: A sample of gas occupies 10 litre under a pressure of 1 atmosphere. What will be its volume if the pressure is increased to 2 atmospheres? Assume that the temperature of the gas sample does not change.
Solution: Mass and temperature is constant hence we can use Boyle's law
P1V1 = P2V2
Given P1 = 1 atm, V1 = 10 litre, P2 = 2 atm, V2 = ?
1 × 10 = 2 × V2 ⇒ V2 = 5 litre
(ii) Charles' Law :
It relates the volume and temperature of a given mass of a gas at constant pressure.
For each degree change of temperature, the volume of a sample of a gas changes by the fraction of its volume at 0 °C.
Let the volume of a given amount of gas be V0 at 0°C. The temperature is increased by t°C and the new volume becomes Vt
Thus , or
A new temperature scale was introduced known as Kelvin scale or absolute scale (named after the British physicist and mathematician Lord Kelvin). The lower limit of the scale is called absolute zero which corresponds to - 273°C.
At absolute zero or - 273 °C , all molecular motions would stop and the volume of the gas would become zero. The gas would become a liquid or solid. Thus, absolute zero is that temperature at which no substance exists in the gaseous state. The temperature in absolute scale is always obtained by adding 273 to the temperature expressed in °C.
K = (t°C 273)
This new temperature scale may be used for deducing Charles' law.
By substituting T for 273 t and T0 for 273 in Eq. (i).
or
or = constant , if pressure is kept constant
(This graph is called isobar)
Alternatively, Charles' law can be stated as follows :
"The volume of a given amount of a gas at constant pressure varies directly as its absolute temperature".
(if pressure is kept constant)
Illustration 3: 1 mole of an ideal gas at constant atmospheric pressure is heated to increase its volume by 50% of initial volume. The change in temperature made was 300 K to T K. Then calculate final temperature.
Solution : At constant pressure for a given amount of gas
Þ
(V1 = V, T1= 300 K, V2 = 1.5V)
T = 450 K
(iii) Pressure-Temperature Law : (Gaylussac's Law)
It relates the pressure and absolute temperature of a given mass of a gas at constant volume.
Volumes remaining constant, the pressure of given mass of a gas increases or decreases by of its pressure at 0°C per degree change of temperature.
Pt = P0 or Pt = P0
or Pt = P0
= P0
or or (if volume and number of moles are kept constant)
At constant volume, the pressure of a given amount of a gas is directly proportional to its absolute temperature.
Illustration 4: Pressure of gas contained in a closed vessel is increased by 0.4%, when heated by 1ºC. Calculate its final temperature. Assume ideal nature.
Solution : Since no information is given about volume hence we can assume that volume is constant and use =
given P1 = P, T1 = T, P2 = P = 1.004 P, T2 = T 1
=
⇒ T = 250 K
(iv) Avogadro's Law
(i) For Solid, liquid and gas
1 mole of any substance contains Avogadro's number (NA) of molecules/atoms/particles etc.
NA = 6.023 × 1023
(ii) For gases:
In 1812, Amadeo Avogadro stated that samples of different gases which contain the same number of molecules (any complexity, size, shape) occupy the same volume at the same temperature and pressure. It follows from Avogadro's hypothesis that (T and P are constant).
(T, P constant) Þ
STP : 273.15 K 1 atm
SATP : 298.15 K 1 bar
(v) Ideal Gas Equation
Combining all these gas laws , a simple equation can be derived at, which relates P , V , n and T for a gas
PV = nRT (for n moles of gas)
⇒ =
(combined gas law)
P is the pressure of the gas and can be expressed in atm or Pa . Correspondingly , the volume must be expressed in litres or m3 respectively. n is the number of moles and T is the temperature in Kelvin. R is called the universal gas constant.
Numerical Values of R
(i) In litre atmosphere = 0.0821 litre atm deg-1 mole-1
(ii) In ergs
(iii) In joules = 8.314 jouls deg-1 mol-1
(iv) In calories =
Illustration 5 : An open vessel at 27°C is heated until 3/5th of the air in it has been expelled. Assuming that the volume of the vessel remains constant find
(A) the air escaped out if vessel is heated to 900K.
(B) temperature at which half of the air escapes out.
Solution : One should clearly note the fact that on heating a gas in a vessel, there are the number of moles of gas which go out, the volume of vessel remains constant.
Let initial no. of moles of gas at 300 K be `n'. On heating 3/5 moles of air escape out at temperature T.
Moles of air left at temperature
(A) On heating vessel to 900 K, let n1 moles be left,
n1T1 = n2T2 ⇒ n1
moles escaped out =
moles
(B) Let n/2 moles escape out at temperature T, then
n1 T1 = n2 T2 Þ Þ T = 600 K
Illustration 6 : 5g of ethane is confined in a bulb of one litre capacity. The bulb is so weak that it will burst if the pressure exceeds 10 atm. At what temperature will the pressure of gas reach the bursting value?
Solution: PV = nRT Þ 10 ×1 = × 0.082 × T
T = = 60 × 12.18 = 730.81 K = 457.81ºC
(vi) Relation between Molecular Mass and Gas Densities
(A) Actual density : For an ideal gas PV = nRT or , where w = mass of the gas in gms and M = Molecular wt. in gms.
or PM = RT, (where is the density of the gas =
(i) =
(for same gas at different temperatrue and pressure)
(ii) =
(for different gases at same temperature & pressure)
(Where d = density of gas)
Illustration 7: The density of an unknown gas at 98°C and 0.974 atm is 2.5 × 10-3g/ml. What is the mol wt. of gas?
Solution: Density = g/ml = 2.5 g/L
PM =
RT
0.974 × M = 2.5 × 0.0821 × 371 M = 78.18.
(B) Vapour Density: For gases another term which is often used is vapour-density. Vapour density of a gas is defined as the ratio of the mass of the gas occupying a certain volume at a certain temperature and pressure to the mass of hydrogen occupying the same volume at the same temperature and pressure i.e. W (gas) = .
and mol. wt. of hydrogen is 2)
(Vapour density of gas)
Vapour density of a gas is same at any temperature, pressure and volume.
Illustration 8: When 3.2 g of sulphur is vapourised at 450°C and 723 mm pressure, the vapours occupy a volume of 780 ml. What is the molecular formula of sulphur vapours under these conditions? Calculate the vapour density also.
Solutlon: PV = nRT ⇒ ×
=
× 0.082 × 723
M = 255.9
no. of catoms of sulpher in one molecule = = 8
Molecular formula of sulphur = S8
V. D. = =
⇒ 127.99
(vii) Dalton's Law of Partial Pressures:
The total pressure of a mixture of non-reacting gases is equal to the sum of their partial pressures.
By Dalton's Law PT = P1 P2 ..............
By the partial pressure of a gas in a mixture is meant, the pressure that the gas will exert if it occupies alone the total volume of the mixture at the same temperature.
Derivation: n = n1 n2 …
Þ
⇒ P = P1 P2 …
Assumption: Volume of all the gases is same as they are kept in same container.
Relationship between partial pressure and number of moles
Important formula
(i) where x1 = mole fraction of gas
(ii) Partial pressure of a gas in the mixture
Partial pressure and aqueous tension: Dalton's law is used to calculate the pressure of a dry gas when it is collected over water at atmospheric pressure.
By Dalton's law,
Pressure of dry gas = atmospheric pressure - aqueous tension
Aqueous tension depends on temperature. It increases with temperature and becomes 760 mm at 100°C.
Illustration 9: A gaseous mixture contains 55% N2, 20% O2, and 25% CO2 by mass at a total pressure of 760 mm. Calculate the partial pressure of each gas.
Solution: Total mass of the gases = 100 g
= 55g,
= 20 g,
= 25g
= 55/28 = 1.964,
= 20/32 = 0.625,
= 25/44 = 0.568
Total moles = 3.157
Illustration 10: A mixture containing 1.6 g of O2, 1.4g of N2 and 0.4 g of He occupies a volume of 10 litre at 27°C. Calculate the total pressure of the mixture and partial pressure of each compound.
Solution: PV = nRT V = 10 litre T = 27ºC = 300K
=
= 0.1,
=
= 0.05,
=
= 0.05
Total no. of moles = 0.1 0.05 0.05 Þ 0.2
PV = nRT
P× 10 = 0.2 × 0.082 × 300 = 0.04926
P = 0.492 atm
Partial pressure = Total pressure × molefraction
PHe = 0.492 × = 0.246 atm
= 0.492 ×
= 0.123 atm
= 0.492 ×
= 0.123 atm
(viii) Graham's Law of Diffusion
Diffusion is the tendency of any substance to spread throughout the space available to it. Diffusion will take place in all direction and even against gravity.
The streaming of gas molecules through a small hole is called effusion.
According to Graham, the rate of diffusion (or effusion) of a gas at constant pressure and temperature is inversely proportional to the square root of its molecular mass.
, at constant P and T
, at constant P and T
Since molecular mass of gas = 2 × vapour density, , at constant P and T
The rate of diffusion (or effusion) r of two gases under different pressure can be given by
at constant T only.
Therefore, according to Graham's law of diffusion (effusion) at constant P and T.
d1 and d2 are the respective densities and V1 and V2 are volumes diffused (effused) in time t1 and t2.
where n1, n2 are moles diffused (effused) in time t1 and t2.
where x1 and x2 are distances travelled by molecules in narrow tube in time t1 and t2.
r =
=
=
Note: It should be noted that the rate of diffusion or effusion actually depends on pressure difference of the gas and not simply on its pressure. Moreover the pressure difference is to be measured for this gas only i.e. if a container holds [He] at a pressure of 0.1 atm and if a small pin-hole is made in the container and if the container is placed in a room, then the rate of effusion of He gas from the container to outside depends only on its pressure difference, which is 0.1-0 (as their is no He in the atmosphere). This implies that the diffusion of a gas is not dependent on the diffusion of any other gas.
Whenever we consider the diffusion of gas under experimental conditions, we always assume that the gas diffuses in vacuum and during the time period for which the diffusion is studied the rate of diffusion (or the composition of diffusing or effusing mixture of gases) remains constant.
Illustration 11: Pure O2 diffuses through an aperture in 224 seconds, whereas mixture of O2 and another gas containing 80% O2 diffuses from the same in 234 sec under similar condition of pressure and temperature. What is molecular wt. of gas?
Solution: The gaseous mixture contains 80% O2 and 20% gas.
Average molecular weight of mixture
… (i)
Now for diffusion of gaseous mixture and pure O2
or
… (ii)
By (i) and (ii) mol weight of gas (m) =46.6.
Illustration 12: Calculate the relative rates of diffusion of 235UF6 and 238UF6 in the gaseous state (Atomic mass of F = 19).
Solution and
(at F = 19)
=
=
= 1.0042
4. The Kinetic Theory of Gases
In order to derive the theoretical aspect of the various gas laws based on simple experiment facts, Maxwell proposed the following postulates under the heading of kinetic theory of gases:
The postulates of kinetic theory of gas are
(i) Each gas is made up of a large number of small (tiny) particles known as molecules.
(ii) The volume of a molecule is so small that it may be neglected in comparison to total volume of gas.
(iii) The molecules are never in stationary state but they are believed to be in chaotic (random) motion. They travel in straight line in all possible directions with altogether different but constant velocities. The direction of motion is changed by the collision with container or with the other molecules.
(iv) The collision between molecules is perfectly elastic i.e., there is no change in the energies of the molecules after collision.
(v) The effect of gravity on molecular motion is negligible.
(vi) The kinetic energy of the gases depends on the temperature.
(vii) The pressure of the gas arises due to collision of molecules with the walls of the container.
The Kinetic Equation : Maxwell also derived an equation on the basis of above assumptions as
PV = mnu2 where
P = Pressure of gas
V = Volume of gas
m = mass of one molecule of gas
n = no. of molecules of gas
u = root mean square velocity of molecules
For 1 mole n = N (Avogadro number)
m × N = Molecular mass M.
or
5. Distribution of Molecular Velocities
Maxwell and Boltzmann proposed that gas molecules are always in rapid random motion colliding with each other and with the walls of container. Due to such collisions, their velocities always changes. A fraction of molecules have a particular molecular velocity at a time. James Clark Maxwell calculated the distribution of velocity among fraction of total number of molecules, on the basis of probability.
The distribution of velocities of different gas molecules may be shown by the following curve.
From the curve it may be concluded that
(i) Only a small fraction of molecules have either very low or very high velocity.
(ii) Curve becomes flat when temperature is raised i.e. distribution around average velocity becomes wider. Average molecular velocity increases with rise in temperature.
(iii) Most of the molecules have velocity close to most probable velocity represented by the top of curve.
(iv) At higher temperature greater number of molecules have high velocity, while few molecules have lower velocity.
Average Velocity : As per kinetic theory of gases, each molecule is moving with altogether different velocity. Let `n' molecules be present in a given mass of gas, each one moving with velocity u1,u2, u3, …,un. The average velocity or Uav = average of all such velocity terms.
Average velocity =
Root Mean Square Velocity : Maxwell proposed the term as the square root of means of square of all such velocities.
Also
Most probable velocity: It is the velocity possessed by maximum no. of molecules.
Furthermore
= = 1 : 1.128 : 1.224
Also
Kinetic Energy of Gas: As per kinetic equation PV = 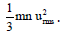
For 1 mole m × n = Molecular Mass (M)
or
Also KE per molecule Where k is the Boltzmann constant
Kinetic Energy of gas sample :
(i) Average kinetic energy of a single molecule = . . T = KT
K = boltzman constant = 1.38 × 10-23 J/deg
(ii) total Kinetic Energy for one mole of gas = RT
(iii) kinetic Energy for n mol of gas = n × RT
Illustration 13: Calculate rms speed of O2 at 273 K and 1 × 105 Pa pressure. The density of O2 under these conditions is 1.42 kg m-3.
Solution: Data are given in SI units
Illustration 14: At what temperature will the r.m.s. velocity of oxygen be one and half times of its value at N.T.P.?
Solution:
Suppose the temperature required is then the velocity will be
Illustration 15: Calculate the average and total kinetic energy of 0.5 mole of an ideal gas at 0°C.
Solution: Average kinetic energy = KT =
×1.38 ×10-23 × 273 = 5.65× 10-21J
Total kinetic energy of n mole of gas = n × RT = 0.5 ×
× 8.314 × 273
= 1.702kJ
6. Deviations from Ideal Behaviour
An ideal gas is one which obeys the gas laws of the gas equation PV = RT at all pressure and temperatures. However no gas in nature is ideal. Almost all gases show significant deviations from the ideal behaviour. Thus the gases H2, N2 and CO2 which fail to obey the ideal-gas equation are termed as non-ideal or real gases.
Compressibility Factor : The extent to which a real gas departs from the ideal behaviour may be depicted in terms of a new function called the compressibility factor, denoted by Z. It is defined as
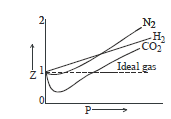
The deviations from ideality may be shown by a plot of the compressibility factor Z, against P.
For an ideal gas, Z = 1 and it is independent of temperature and pressure.
The deviations from ideal behaviour of a real gas will be determined by the value of Z being greater or less than 1.
The difference between unity and the value of the compressibility factor of a gas is a measure of the degree of non ideality of the gas.
For a real gas, the deviations from ideal behaviour depends on :
(i) pressure ; and (ii) temperature.
This will be illustrated by examining the compressibility curves of some gases discussed below with the variation of pressure and temperature.
Effect of Pressure Variation on Deviations:
Effect of Temperature on Deviations:
From the above curves we can conclude that:
1. At low pressure and fairly high temperatures, real gases show nearly ideal behaviour and the ideal-gas equation is obeyed.
2. At low temperatures and sufficiently high pressures, a real gas deviates significantly from ideality and the ideal-gas equation is no longer valid.
3. The closer the gas is to the liquefication point, the larger will be the deviation from the ideal behaviour.
Greater is the departure of Z from unity, more is the deviation from ideal behaviour.
(i) When Z < 1, this implies that gas is more compressible.
(ii) When Z > 1, this means that gas is less compressible.
(iii) When Z = 1, the gas is ideal.
Vander Waals Equation of State for a Real Gas: The equation of state generated by Vander Waals in 1873 reproduces the observed behaviour with moderate accuracy. For n moles of gas, the Vander Waals equation is
(V - nb) = nRT
where a and b are constants characteristic of a gas. This equation can be derived by considering a real gas and converting it to an ideal gas.
Volume Correction : We know that for an ideal gas P × V = nRT. Now in a real gas the molecular volume cannot be ignored and therefore let us assume that `b' is the volume excluded (out of the volume of container) for the moving gas molecules per mole of a gas. Therefore due to n moles of a gas the volume excluded would benb.
a real gas in a container of volume V has only available volume of (V - nb) and this can be thought of, as an ideal gas in a container of volume (V - nb)
Pressure Correction : Let us assume that the real gas exerts a pressure P. The molecules that exert the force on the container will get attracted by molecules of the immediate layer which are not assumed to be exerting pressure.
It can be seen that pressure the real gas exerts would be less than the pressure an ideal gas would have exerted. Therefore if a real gas exerts a pressure P, then an ideal gas would exert a pressure equal to P p(p is the pressure lost by the gas molecules due to attractions). This small pressure p would be directly proportional to the extent of attraction between the molecules which are hitting the container wall and the molecules which are attracting these.
Therefore (concentration of molecules which are hitting the container's wall)
(concentration of molecules which are attracting these molecules )
where a is the constant of proportionality which depends on the nature of gas. Higher value of `a' reflects the increased attraction between gas molecules.
The Vander Waals constant b (the excluded volume) is actually 4 times the volume of a single molecule. i.e. b = 4 NAV where NA → Avogadro number.
b = 4 × 6.023 × 1023
, where r is the radius of a molecule.
The constant a and b: Vander Waals constant for attraction (A) and volume (B) are characteristic for a given gas. Some salient features of `a' and `b' are:
(i) For a given gas Vander Waal's constant of attraction `a' is always greater than Vander Waals constant of volume (B).
(ii) The gas having higher value of `a' can be liquified easily and therefore H2 and He are not liquified easily.
(iii) The units of a = litre2 atm mole-2 and that of b = litre mole-1
(iv) The numerical values of a and b are in the order of 10-1 to 10-2 to 10-4respectively.
(v) Higher is the value of `a' for a given gas, easier is the liquification.
Explanation of deviation by Van der Waals equation
(i) At lower pressure : `V' is large and `b' is negligible in comparison with V.
Then Vander Waals equation reduces to :
Þ
⇒ Z =
= 1 -
or PV < RT at low pressure (below Boyle temperature)
this accounts for the dip in PV vs P isotherm at low pressure.
(ii) At fairly high pressures : may be neglected in comparison with P.
The Vander Waals equation becomes
P ( V-b) = RT ⇒ PV - Pb = RT
PV = RT + Pb ⇒ Z = = 1
or PV > RT at higher pressure (above Boyle temperature)
This accounts for the rising parts of the PV vs P isotherm at high pressures.
(iii) At very low pressure : V becomes so large that both b and become negligible and the Vander Waals equation reduces to PV = RT
z = = 1 ; Pb =
At extremely low pressure (at Boyle temperature)
This shows why gases approach ideal behaviour at very low pressures.
(iv) Hydrogen and Helium : These are two lightest gases known. Their molecules have very small masses. The attractive forces between such molecules will be extensively small. So is negligible even at ordinary temperatures. Thus PV > RT.
Dieterici Equation :
P (V - nb) = n R T ea/VRT (for `n' mole of a gas)
Berthelot Equation :
(V - nb) = n R T
Virial Equation Of State For 1 Mole Of Gas :
z = = 1 B
C
D
..............
B = second virial co-efficient , temperature dependent = b -
C = third virial co - efficient, temperature dependent = b2
Illustration 16 : The compressibility factor for 1 mole of a van der Waals gas at 0ºC and 100 atm pressure is found to be 0.5. Assuming that the volume of a gas molecule is negligible, calculate the van der Waals constant, a.
Solution: For 1 mole of the gas,
Z = Þ 0.5 =
; V = 0.112 L
Neglecting b, van der Waals equation reduces to V = RT
or pV = RT
or 100 × 0.112 = .0821 × 273
a = 1.25 L2atm mol-2
7. Critical phenomenon & Liquification of gases
The phenomena of converting a gas into liquid is known as liquifaction. The liquifaction of gas is achieved by controlling P and T as follows:
1. Increasing pressure : An increase in pressure results in an increase in attraction among molecules.
2. Decreasing temperature : A decrease in temperature results in decrease in kinetic energy of molecules.
Critical temperature (Tc) : It is defined as the characteristic temperature for a given gas below which a continuous increase in pressure will bring liquification of gas and above which no liquefaction is noticed although pressure may be increased e.g. Tc for CO2 is 31.2°C.
TC =
Critical pressure (Pc) : It is defined as the minimum pressure applied on 1 mole of gas placed at critical temperature, to just liquefy the gas
PC =
Critical Volume (Vc) : The volume occupied by 1 mole of gas placed at critical conditions.
VC = 3b (i.e. P = Pc and T = Tc)
8. Collision parameters
- Mean free path
=
(
= coefficient of viscosity)
=
k = Boltzman constant ; = collision diameter.
- Collision frequency (z) : no. of collision taking place per second per unit volume.
- Collision diameter : Closest distance between the centre of two molecule which are participating in collision.
- Relative Humidity (RH) :
At a given temperatrue
RH =
- Loschmidth Number
The number of molecules present in 1 cc of gas (or) vapour at STP.
value : 2.617 × 1019 1 cc
solved Examples
Ex.1 When 2 gm of a gaseous substance A is introduced into an initially evacuated flask at 25°C, the pressure is found to be 1 atm. 3 gm another gaseous substance B is then added to it at the same temperature and pressure. The final pressure is found to be 1.5 atm. Assuming ideal gas behaviour, calculate the ratio of the molecular weights of A and B.
Sol. Let MA and MB be the molecular weights of A and B.
Using PV = nRT for A, we get :
...(i)
and using Dalton's Law : PTotal = Þ 1.5 =
...(ii)
Solving (i) and (ii), we get
Ex.2 Which of the two gases, ammonia and hydrogen chloride, will diffuse faster and by what factor ?
Sol. By Graham's Law :
Þ
Thus, ammonia will diffuse 1.46 times faster than hydrogen chloride gas.
Ex.3 The ratio of rate of diffusion of gases A and B is 1 : 4 and their molar mass ratio is 2 : 3. Calculate the composition of the gas mixture intially effusing out.
Sol. By Graham's Law :
Þ
Þ
Þ Mole ratio of gas A and B effusing out = [moles µ pressure]
Ex.4 At 30°C and 720 mm of Hg, the density of a gas is 1.5 g/lt. Calculate molecular mass of the gas. Also find the number of molecules in 1 cc of the gas at the same temperature.
Sol. Assuming ideal behaviour and applying ideal gas equation :
PV = nRT
Another form of gas equation is PM0 = dRT
Þ M0 = =
(T = 30 273 K)
Þ M0 = 39.38
Now number of molecules = n × N0
= 2.29 × 1019
Ex.5 The pressure exerted by 12 gm of an ideal gas at temperature t°C in a vessel of volume V litre is one atm. When the temperature is increased by 10° at the same volume, the pressure rises by 10% calculate the temperature t and volume V. (molecular mass of the gas = 120 gm/mole)
Sol. Using Gas equation : PV = nRT
We have, P × V = 0.1 × R × t ...(1)
and 1.1 P × V = 0.1 × R × (t 10) ...(2)
Using (i) and (ii), we have :
Þ t = 100 k or t = - 173°C
Putting the value of t in (i), we get :
⇒ 1 × V = 0.1 × 0.0821 × 100
⇒ V = 0.821 L
Ex.6 Assuming that the air is essentially a mixture of nitrogen and oxygen in mole ratio of 4 : 1 by volume. Calculate the partial pressures of N2 and O2 on a day when the atmospheric pressure is 750 mm of Hg. Neglect the pressure of other gases.
Sol. From Dalton's Law of partial pressure, we have
Partial pressure of nitrogen = × P and Partial pressure of oxygen =
Now, , and
⇒ × 750 = 600 mm of Hg and
= 150 mm of Hg
Ex.7 An open vessel at 27°C is heated until three fifth of the air has been expelled, Assuming that the volume of the vessel remains constant, find the tempeature to which the vessel has been heated.
Sol. In the given questions, volume is constant. Also, as the vessel is open to atmosphere, the pressure is constant. This means that the gas equation is simply reduced to the following form :
nT = constant (Use PV = nRT)
or n1 T1 = n2 T2
Now let n1 = initial moles and n2 = final moles
Þ n2 = 2/5 × n1 (as 3/5th of the air has been expelled)
Þ T2 = =
=
Þ T2 = = 750 K = 477°C
Ex.8 When 3.2 gm of sulphur is vaporized at 450° C and 723 mm pressure, the vapour occupies a volume of 780 m, what is the formula for the sulphur under these conditions ?
Sol. The molecular weight = no. of atoms × atomic mass
So let us find the molecular weight of S from the data given.
Þ Number of atoms =
Hence, molecular formula of sulphur = S8
Ex.9 A spherical ballon of 21 cm diameter is to be filled with H2 at NTP from a cylinder containing the gas at 20 atm at 27°C. If the cylinder can hold 2.80L of water, calculate the number of ballons that can be filled up.
Sol. The capacity of cylinder = 2.80 L
Let n = moles of hydrogen contained in cylinder and n0 = moles of hydrogen required to fill one balloon.
n =
(Note : the balloons are being filled at S.T.P.)
= =
Þ Number of balloons that can be filled = » 10
Ex.10 A mixture containing 1.12L of H2 and 1.12L of D2 (deuterium) at S.T.P. is taken inside a bulb connected to another bulb by a stop-cock with a small opening. The second bulb is fully evacuated; the stop-cock is opened for a certain time and then closed. The first bulb is found to contain 0.05 gm of H2. Determine the % age composition by weight of the gases in the second bulb.
Sol. In the first bulb :
Initial moles of H2 = 1.12 / 22.4 = 1/20
Initial moles of D2 = 1.12/22.4 = 1/20
Now after opening of stop-cock, mass of H2 left in the first bulb = 0.05
Moles of H2 = 0.05/2 = 1/40
Moles of H2 effused into second bulb = 1/20 - 1/40 = 1/40
Let n be number of moles of D2 effused.
From Graham's Law :
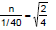
= moles of D2 in second bulb.
In the second bulb :
The mass of H2 gas = 1/40 × 2 = 0.05 gm
The mass of D2 gas = Ö2/80 × 4 = 0.07 gm
Þ Total mass = 0.05 0.07 = 0.12 gm
Þ % of H2 = 0.05/1.12 × 100 = 41.67 %
Þ % of D2 = 0.07/1.12 × 100 = 58.13 %
Ex.11 The pressure in a bulb dropped from 2000 mm to 1500 mm of Hg in 47 min when the contained O2 leaked through a small hole. The bulb was then completely evacuated. A mixture of oxygen and another gas (B) of molecular weight 79 in the molar ratio of 1 : 1 at a total pressure of 4000 mm of Hg was introduced. Find the molar ratio of the two gases remaining in the bulb after a period of 74 min.
Sol. Now as P ≈ n (moles), we define the rate of diffusion as the drop in the pressure per second. First we try to find the rate of diffusion of the gas B.
The rate of diffusion of O2 = R0 = (2000 - 1500)/47 = 10.638 mm/min.
Assuming that gas B was present alone in the bulb. Let the rate of dffusion of B = RB.
From Graham's Law of diffusion, we have :
Now the bulb contains mixture of O2 and B in the mole ration of 1 : 1 at total pressure of 4000 mm Hg.
of Hg
As the pressure and temperature conditions are same for both gases in the second case (same bulb), so the rate of diffusion will remain same in the second case also.
Let X0 and XB be the final pressure in the bulb after leakage for 74 minutes.
As P ≈ n
Ratio of moles is given as : XO : XB = 1 : 1235
Ex.12 A 672 ml of a mixture of oxygen-ozone at N.T.P. were found to be weigh 1 gm. Calculate the volume of ozone in the mixture.
Sol. Let V ml of ozone are there in the mixture
(672 - V) m; = vol. of oxygen
Mass of ozone at N.T.P. =
Mass of oxygen at N.T.P.
Ex.13 A 20 L flask contains 4.0 gm of O2 & 0.6 gm of H2 at 100º C. If the contents are allowed to react to form water vapors at 100º C, find the contents of flask and there partial pressures.
Sol. H2 reacts with O2 to form water [H2O(g)]
2 moles of H2 = 1 mole of O2 = 2 moles of H2O
Here masses of H2 and O2 are given, so one of them can be in excess. So first check out which of the reactants is in excess.
Now, Moles of O2 = 4/32 = 0.125 and Moles of H2 = 0.6/2 = 0.3
Since 1 mole of O2 º 2 moles of H2
0.125 moles of O2 º 2 × 0.125 moles of H2
i.e. 0.25 moles of H2 are used, so O2 reacts completely whereas H2 is in excess.
Moles of H2 in excess = 0.3 - 0.25 = 0.05 moles.
Also, 2 moles of H2 º 2 moles of H2O
0.25 moles of H2 º 0.25 moles of H2O are produced.
Total moles after the reaction = 0.05 (moles of H2) 0.25 (moles of H2O) = 0.3
The total pressure PTotal at the end of reaction is given by :
Now partial pressure of A = mole fraction of A × PTotal
Ex.14 The compressibility factor for 1 mole of a van Waals gas at 0ºC and 100 atm pressure is found to be 0.5. Assuming that the volume of gas molecular is negligible, calculate the van der Waals constant `a'.
Using van der Waal's equation of state :
Now : V - nb V(given)
The equation is reduced to :
or
Also,
Substitute the values of V and T :
a = 1.25 litre2 mol-2 atm.
Ex.15 Calculate the pressure exerted by 5 mole of CO2 in one litre vessel at 47ºC using van der waals equation. Also report the pressure of gas if it behaves ideally in nature.
(a = 3.592 atm litre2 mol-2, b = 0.0427 litre mol-1)
Using van der waals equation of state :
Substituting the given values, we get :
If the gas behaves ideally, then using : PV = nRT
FAQs on States of Matter, Chapter Notes, Class 11, Chemistry (IIT-JEE & AIPMT)
| 1. What are the three states of matter? |  |
| 2. What is the difference between a solid and a liquid? |  |
| 3. What is the kinetic theory of matter? |  |
| 4. What is sublimation? |  |
| 5. How is the state of matter affected by pressure and temperature? |  |















