Best Study Material for JEE Exam
JEE Exam > JEE Notes > Mathematics (Maths) for JEE Main & Advanced > NCERT Solutions - Exercise 8.1 : Application of Integral
NCERT Solutions Class 12 Maths Chapter 8 - Application of Integral
Application of Integral
Question 1: Find the area of the region bounded by the ellipse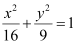 
ANSWER : - The given equation of the ellipse,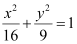 
, can be represented as
It can be observed that the ellipse is symmetrical about x-axis and y-axis.
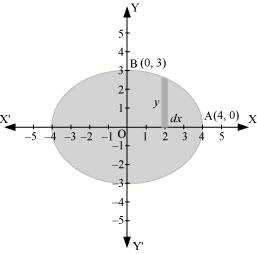
∴ Area bounded by ellipse = 4 × Area of OAB
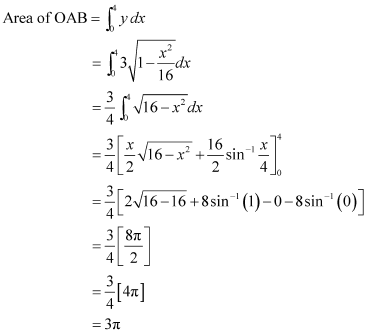
Therefore, area bounded by the ellipse = 4 × 3π = 12π units
Question 2: Find the area of the region bounded by the ellipse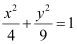 
ANSWER : -The given equation of the ellipse can be represented as
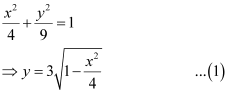
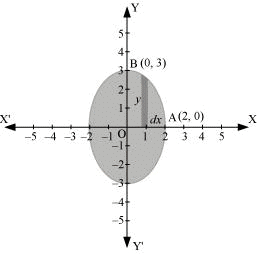
It can be observed that the ellipse is symmetrical about x-axis and y-axis.
∴ Area bounded by ellipse = 4 × Area OAB
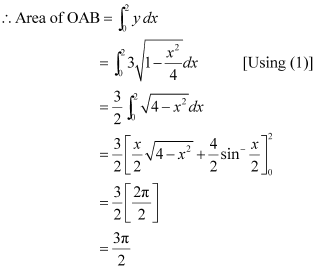
Therefore, area bounded by the ellipse =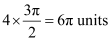 
Question 3: Area lying in the first quadrant and bounded by the circle x2 + y2 = 4 and the lines x = 0 and x = 2 is
A. π
B.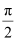 
C.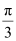 
D.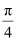 
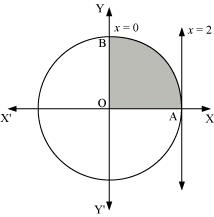
ANSWER : -The area bounded by the circle and the lines, x = 0 and x = 2, in the first quadrant is represented as
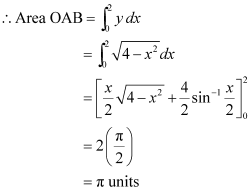
Thus, the correct answer is A.
Question 4: Area of the region bounded by the curve y2 = 4x, y-axis and the line y = 3 is
A. 2
B.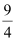 
C.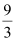 
D.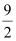 
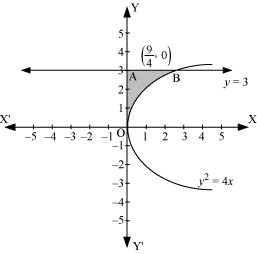
ANSWER : - The area bounded by the curve, y2 = 4x, y-axis, and y = 3 is represented as
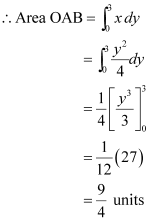
Thus, the correct answer is B.
The document NCERT Solutions Class 12 Maths Chapter 8 - Application of Integral is a part of the JEE Course Mathematics (Maths) for JEE Main & Advanced.
All you need of JEE at this link: JEE
|
209 videos|447 docs|187 tests
|
FAQs on NCERT Solutions Class 12 Maths Chapter 8 - Application of Integral
| 1. What is the application of integrals? |  |
| 2. How do integrals help in finding areas? | |
Ans. Integrals help in finding areas by dividing the region into small rectangles or trapezoids, calculating the area of each small portion, and then adding them up using the concept of integration. This method is called the definite integral and is denoted by the symbol ∫.
| 3. Can integrals be used to determine the volume of irregular shapes? | |
Ans. Yes, integrals can be used to determine the volume of irregular shapes. By applying the concept of integration to three-dimensional figures, we can calculate the volume of irregular shapes such as cones, spheres, and pyramids.
| 4. What are the real-life applications of integrals? | |
Ans. Integrals have numerous real-life applications. They are used in physics to calculate the work done by a force, in economics to determine the total revenue and cost functions, in biology to model population growth, and in statistics to find the probability distribution functions.
| 5. How are integrals used in optimization problems? | |
Ans. Integrals are used in optimization problems to find the maximum or minimum value of a function. By setting up an appropriate equation and using the techniques of calculus, we can solve optimization problems to determine the optimal solution for various scenarios, such as maximizing profit or minimizing cost.
Related Exams
About this Document
3.7K Views
4.69/5
Rating
Apr 11, 2025
Last updated
Document Description: NCERT Solutions - Exercise 8.1 : Application of Integral for JEE 2025 is part of Mathematics (Maths) for JEE Main & Advanced preparation.
The notes and questions for NCERT Solutions - Exercise 8.1 : Application of Integral have been prepared according to the JEE exam syllabus. Information about NCERT Solutions - Exercise 8.1 : Application of Integral covers topics
like and NCERT Solutions - Exercise 8.1 : Application of Integral Example, for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for NCERT Solutions - Exercise 8.1 : Application of Integral.
Introduction of NCERT Solutions - Exercise 8.1 : Application of Integral in English is available as part of our Mathematics (Maths) for JEE Main & Advanced
for JEE & NCERT Solutions - Exercise 8.1 : Application of Integral in Hindi for Mathematics (Maths) for JEE Main & Advanced course.
Download more important topics related with notes, lectures and mock test series for JEE
Exam by signing up for free. JEE: NCERT Solutions Class 12 Maths Chapter 8 - Application of Integral
Description
Full syllabus notes, lecture & questions for NCERT Solutions Class 12 Maths Chapter 8 - Application of Integral - JEE | Plus excerises question with solution to help you revise complete syllabus for Mathematics (Maths) for JEE Main & Advanced | Best notes, free PDF download
Information about NCERT Solutions - Exercise 8.1 : Application of Integral
In this doc you can find the meaning of NCERT Solutions - Exercise 8.1 : Application of Integral defined & explained in the simplest way possible. Besides explaining types of
NCERT Solutions - Exercise 8.1 : Application of Integral theory, EduRev gives you an ample number of questions to practice NCERT Solutions - Exercise 8.1 : Application of Integral tests, examples and also practice JEE
tests
Related Searches
past year papers
,NCERT Solutions Class 12 Maths Chapter 8 - Application of Integral
,Important questions
,mock tests for examination
,video lectures
,Previous Year Questions with Solutions
,Sample Paper
,Free
,Semester Notes
,Extra Questions
,Viva Questions
,Summary
,ppt
,Objective type Questions
,Exam
,study material
,NCERT Solutions Class 12 Maths Chapter 8 - Application of Integral
,shortcuts and tricks
,practice quizzes
,MCQs
,NCERT Solutions Class 12 Maths Chapter 8 - Application of Integral
;
Additional Information about NCERT Solutions - Exercise 8.1 : Application of Integral for JEE Preparation
NCERT Solutions - Exercise 8.1 : Application of Integral Free PDF Download
The NCERT Solutions - Exercise 8.1 : Application of Integral is an invaluable resource that delves deep into the core of the JEE exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the NCERT Solutions - Exercise 8.1 : Application of Integral now and kickstart your journey towards success in the JEE exam.
Importance of NCERT Solutions - Exercise 8.1 : Application of Integral
The importance of NCERT Solutions - Exercise 8.1 : Application of Integral cannot be overstated, especially for JEE aspirants.
This document holds the key to success in the JEE exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
NCERT Solutions - Exercise 8.1 : Application of Integral Notes
NCERT Solutions - Exercise 8.1 : Application of Integral Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to NCERT Solutions - Exercise 8.1 : Application of Integral.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, NCERT Solutions - Exercise 8.1 : Application of Integral Notes on EduRev are your ultimate resource for success.
NCERT Solutions - Exercise 8.1 : Application of Integral JEE Questions
The "NCERT Solutions - Exercise 8.1 : Application of Integral JEE Questions" guide is a valuable resource for all aspiring students preparing for the
JEE exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study NCERT Solutions - Exercise 8.1 : Application of Integral on the App
Students of JEE can study NCERT Solutions - Exercise 8.1 : Application of Integral alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the NCERT Solutions - Exercise 8.1 : Application of Integral,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of NCERT Solutions - Exercise 8.1 : Application of Integral is prepared as per the latest JEE syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily