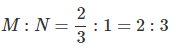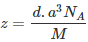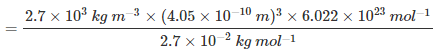The Solid State - 1 (Old NCERT) NCERT Solutions | Chemistry for JEE Main & Advanced PDF Download
The chapter on "The Solid State" introduces students to the fundamental principles governing the physical and chemical properties of solids. Let us have a look at NCERT Solutions of the chapter:

Intext Questions
Question 1.1: Why are Solids rigid?
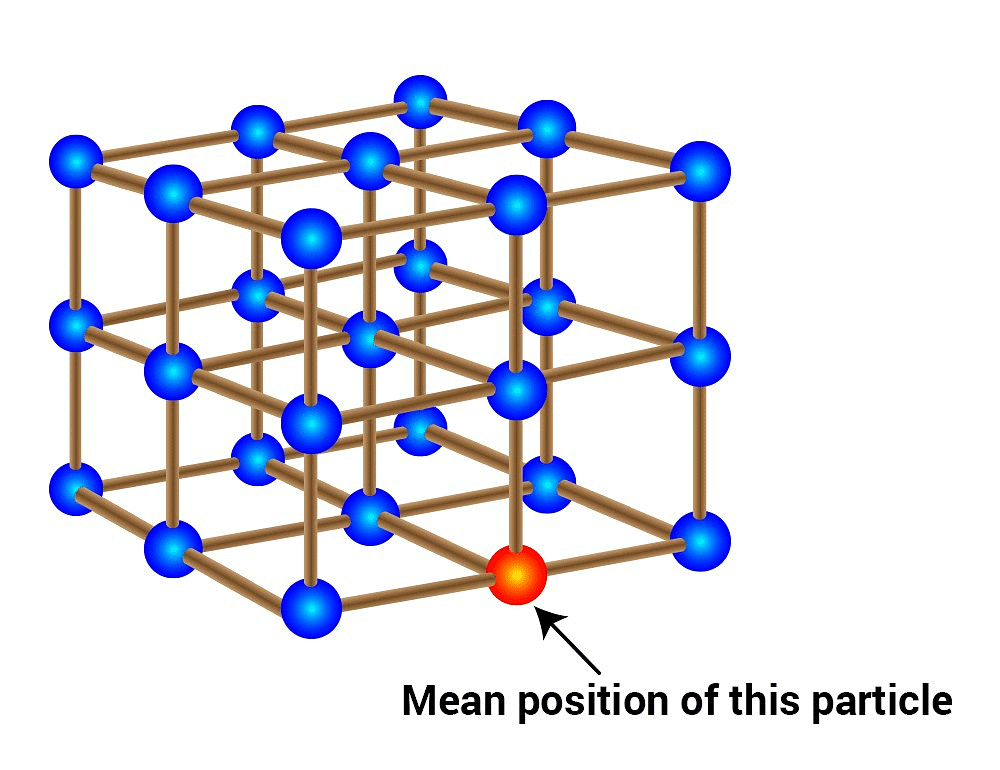
- Interatomic or intermolecular forces: Solids are rigid because their constituent particles, such as atoms, molecules, or ions, are held together by strong interatomic or intermolecular forces. These forces prevent the particles from moving past one another, which would result in a deformation of the solid.
Fixed positions of particles: In a solid, the particles are tightly packed and have fixed positions relative to one another. When a force is applied to a solid, the particles vibrate slightly around their fixed positions, but they do not move out of their positions. This gives solids their characteristic shape and volume.
Vibrational motion of particles: Furthermore, the rigidity of solids can also be attributed to their high density, which means that there are a large number of particles per unit volume, making it more difficult for them to move past one another.
Overall, the strong interatomic or intermolecular forces, fixed positions of particles, and high density of solids combine to make them rigid.
Question 1.2: Why do Solids have a definite volume?
Solids have a definite volume because the particles that make up a solid are closely packed together and held in place by strong interatomic or intermolecular forces. These forces are much stronger than those in liquids or gases, which allows the particles to move around freely and take the shape of their container.
- Fixed arrangement of particles: In contrast, the particles in a solid are unable to move around freely, and they vibrate around fixed positions. This fixed arrangement of particles gives the solid its definite shape and volume.
- Different from liquid and gas: When a solid is placed in a container, the particles cannot move past each other and fill the entire container, like a gas or liquid would. Instead, they maintain their fixed positions and occupy a specific volume within the container.
Therefore, solids have a definite shape and volume, which sets them apart from liquids and gases that can change their shape and volume based on their container's shape and size.
Question 1.3: Classify the following as Amorphous or Crystalline Solids:
Polyurethane, Naphthalene, Benzoic acid, Teflon, Potassium Nitrate, Cellophane, Polyvinyl Chloride, Fibreglass, Copper.
Here is the classification of the given solids as amorphous or crystalline:
- Polyurethane - Amorphous solid
- Naphthalene - Crystalline solid
- Benzoic acid - Crystalline solid
- Teflon - Amorphous solid
- Potassium Nitrate - Crystalline solid
- Cellophane - Amorphous solid
- Polyvinyl Chloride - Amorphous solid
- Fibreglass - Amorphous solid
- Copper - Crystalline solid
Explanation:
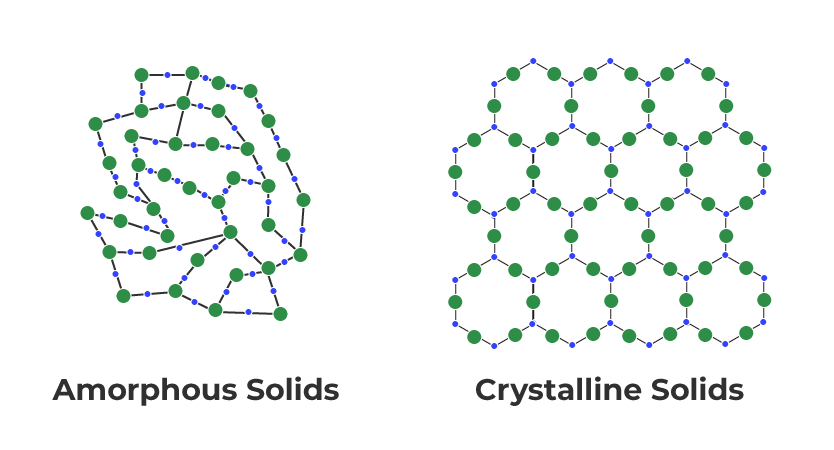
- Crystalline solids: Crystalline solids have a regular, repeating arrangement of particles in a three-dimensional pattern, known as a crystal lattice structure. They have a sharp melting point, and their properties are uniform in all directions.
- Amorphous solids: Amorphous solids, on the other hand, do not have a regular pattern or crystal lattice structure. They have a broad melting point range and do not have a specific shape or structure.
Based on these characteristics, we can classify the given solids as amorphous or crystalline. Polyurethane, Teflon, Cellophane, and Polyvinyl Chloride are amorphous solids, while Naphthalene, Benzoic acid, Potassium Nitrate, and Copper are crystalline solids.
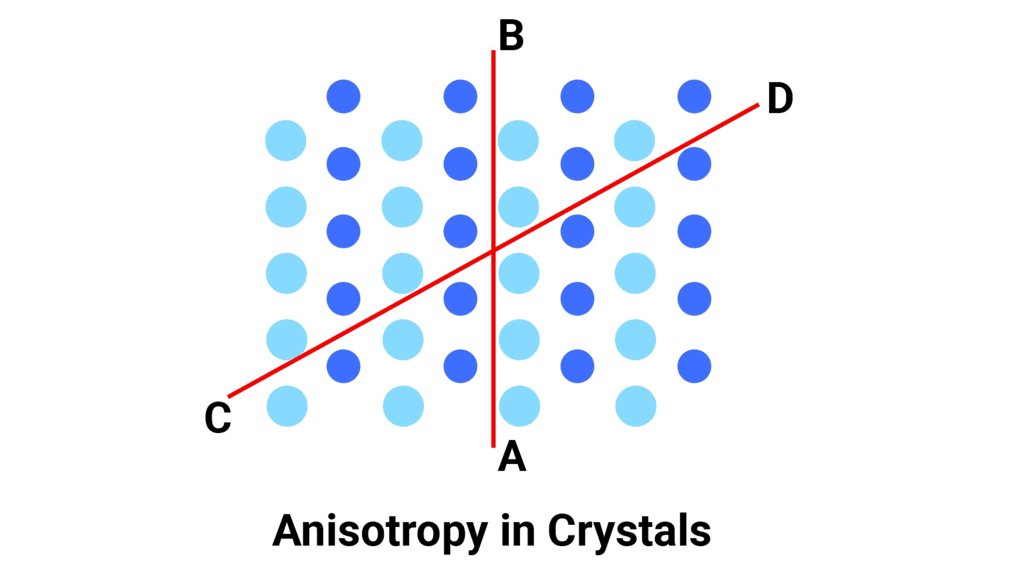
Question 1.4: Refractive index of a solid is observed to have the same value along all directions. Comment on the nature of this solid. Would it show cleavage property?
- If a solid has the same refractive index along all directions, it is called an isotropic solid. This means that the solid looks the same from all directions and has no preferred direction of symmetry. Examples of isotropic solids include glasses and some plastics.
- However, isotropic solids do not have a regular arrangement of atoms or molecules, which means they do not have cleavage planes. Cleavage planes are planes along which a crystal can easily split, producing flat surfaces. Instead, isotropic solids break irregularly when subjected to external force, which is called fracture.
Question 1.5: Classify the following solids in different categories based on the nature of intermolecular forces operating in them:
Potassium sulphate, tin, benzene, urea, ammonia, water, zinc sulphide, graphite, rubidium, argon, silicon carbide.
- Potassium sulphate → Ionic solid
- Tin → Metallic solid
- Benzene → Molecular (non-polar) solid
- Urea → Polar molecular solid
- Ammonia → Polar molecular solid
- Water → Hydrogen bonded molecular solid
- Zinc sulphide → Ionic solid
- Graphite → Covalent or network solid
- Rubidium → Metallic solid
- Argon → Non-polar molecular solid
- Silicon carbide → Covalent or network solid
Question 1.6: Solid A is a very hard electrical insulator in solid as well as in molten state and melts at extremely high temperature. What type of solid is it?
The given properties are the properties of a covalent or network solid. Therefore, the given solid is a covalent or network solid. Examples of such solids include diamond (C) and quartz (SiO2).
Question 1.7: Ionic solids conduct electricity in molten state but not in solid state. Explain.
In ionic compounds, electricity is conducted by ions. In solid state, ions are held together by strong electrostatic forces and are not free to move about within the solid. Hence, ionic solids do not conduct electricity in solid state. However, in molten state or in solution form, the ions are free to move and can conduct electricity.
Question 1.8: What type of solids are electrical conductors, malleable and ductile?
Metallic solids are electrical conductors, malleable, and ductile.
Question 1.9: Give the significance of a ‘lattice point’.
The significance of a lattice point is that each lattice point represents one constituent particle of a solid which may be an atom, a molecule (a group of atoms), or an ion.
Question 1.10: Name the parameters that characterize a unit cell.
Following parameters characterized the unit cell:
(a) Its dimensions along the three edges a, b, and c.
These edges may or may not be equal.
(b) Angles between the edges
These are the angle ∝ (between edges b and c), β (between edges a and c), and γ (between edges a and b).Parameters of a Unit Cell
Question 1.11: Distinguish between
(i) Hexagonal and Monoclinic unit cells
(ii) Face-centred and End-centred unit cells.
(i) Hexagonal and Monoclinic unit cells
- Hexagonal unit cell:
For a hexagonal unit cell,
a = b ≠ c, and α = β = c, and α = β = 90°
γ = 120°
Hexagonal Packing
- Monoclinic unit cell:
For a monoclinic cell,
a ≠ b ≠ c, and α = γ = 90°
β ≠ 90°(ii) Face-centred and End-centred unit cells
- Face-centred unit cells:
In a face-centred unit cell, the constituent particles are present at the corners and one at the centre of each face.- End-centred unit cells:
An end-centred unit cell contains particles at the corners and one at the centre of any two opposite faces.
Question 1.12: Explain how much portion of an atom located at the corner and body-centre of a cubic unit cell is part of its neighbouring unit cell.
- An atom located at the corner of a cubic unit cell is shared by eight adjacent unit cells. Therefore,
portion of the atom is shared by one unit cell.
- An atom located at the body centre of a cubic unit cell is not shared by its neighbouring unit cell. Therefore, the atom belongs only to the unit cell in which it is present i.e., its contribution to the unit cell is 1.
Question 1.13: What is the two-dimensional coordination number of a molecule in the square close-packed layer?
In square close-packed layer, a molecule is in contact with four of its neighbours. Therefore, the two-dimensional coordination number of a molecule in square close-packed layer is 4.
Question 1.14: A compound forms a hexagonal close-packed structure. What is the total number of voids in 0.5 mol of it? How many of these are tetrahedral voids?
Number of close-packed particles = 0.5 × 6.022 × 1023 = 3.011 × 1023
Therefore, the number of octahedral voids = 3.011 × 1023
And, number of tetrahedral voids = 2 × 3.011 × 1023 = 6.022 ×1023
Therefore, the total number of voids = 3.011 × 1023 6.022 × 1023 = 9.033 × 1023
Question 1.15: A compound is formed by two elements M and N. The element N forms ccp and atoms of M occupy 1/3rd of tetrahedral voids. What is the formula of the compound?
The ccp lattice is formed by the atoms of the element N.
Here, the number of tetrahedral voids generated is equal to twice the number of atoms of the element N.
According to the question, the atoms of element M occupy
of the tetrahedral voids. Therefore, the number of atoms of M is equal to
of the number of atoms of N.
Therefore, the ratio of the number of atoms of M to that of N isThus, the formula of the compound is M2N3.
Question 1.16: Which of the following lattices has the highest packing efficiency:
(a) Simple cubic.
(b) Body-centred cubic.
(c) Hexagonal close-packed lattice.
Hexagonal close-packed lattice has the highest packing efficiency of 74%. The packing efficiencies of simple cubic and body-centred cubic lattices are 52.4% and 68% respectively.
Question 1.17: An element with molar mass 2.7 × 10-2 kg mol-1 forms a cubic unit cell with an edge length of 405 pm. If its density is 2.7 × 103 kg m−3, what is the nature of the cubic unit cell?
It is given that density of the element, d = 2.7 × 103 kg m−3
Molar mass, M = 2.7 × 10−2 kg mol−1
Edge length, a = 405 pm = 405 × 10−12 m
= 4.05 × 10−10 m
It is known that, Avogadro’s number, NA = 6.022 × 1023 mol−1Applying the relation,
=4.004
=4This implies that four atoms of the element are present per unit cell. Hence, the unit cell is face-centred cubic (fcc) or cubic close-packed (ccp).
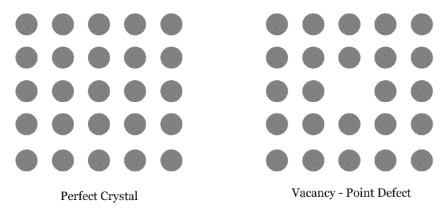
Question 1.18: What type of defect can arise when a solid is heated? Which physical property is affected by it and in what way?
When a solid is heated, vacancy defect can arise.
A solid crystal is said to have vacancy defect when some of the lattice sites are vacant. Vacancy defect leads to a decrease in the density of the solid.
Question 1.19: What type of stoichiometric defect is shown by:
(i) ZnS
(ii) AgBr
(i) ZnS shows Frenkel defect.
(ii) AgBr shows Frenkel defect as well as Schottky defect.
Question 1.20: Explain how vacancies are introduced in an ionic solid when a cation of higher valence is added as an impurity in it.
When a cation of higher valence is added to an ionic solid as an impurity to it, the cation of higher valence replaces more than one cation of lower valence so as to keep the crystal electrically neutral. As a result, some sites become vacant.
Example: When Sr2+ is added to NaCl, each Sr2+ ion replaces two Na ions. However, one Sr2+ ion occupies the site of one Na+ ion and the other site remains vacant. Hence, vacancies are introduced.
Question 1.21: Ionic solids, which have anionic vacancies due to metal excess defect, develop colour. Explain with the help of a suitable example.
The colour develops because of the presence of electrons in the anionic sites. These electrons absorb energy from the visible part of radiation and get excited.
Example: When crystals of NaCl are heated in an atmosphere of sodium vapours, the sodium atoms get deposited on the surface of the crystal and the chloride ions from the crystal diffuse to the surface to form NaCl with the deposited Na atoms. During this process, the Na atoms on the surface lose electrons to form Na+ ions and the released electrons diffuse into the crystal to occupy the vacant anionic sites. These electrons get excited by absorbing energy from the visible light and impart yellow colour to the crystals.
Question 1.22: A group 14 element is to be converted into n-type semiconductor by doping it with a suitable impurity. To which group should this impurity belong?
An n-type semiconductor conducts because of the presence of extra electrons. Therefore, a group 14 element can be converted to n-type semiconductor by doping it with a group 15 element.
Question 1.23: What type of substances would make better permanent magnets, ferromagnetic or ferrimagnetic. Justify your answer.
Ferromagnetic substances would make better permanent magnets.
- In a solid-state, the metal ions of ferromagnetic substances are grouped together into small regions. These regions are called domains and each domain acts as a tiny magnet. In an unmagnetized piece of a ferromagnetic substance, the domains are randomly oriented. As a result, the magnetic moments of the domains get canceled.
- However, when the substance is placed in a magnetic field, all the domains get oriented in the direction of the magnetic field and a strong magnetic effect is produced. The ordering of the domains persists even after the removal of the magnetic field. Thus, the ferromagnetic substance becomes a permanent magnet.
Question 1.24: Why is glass considered a supercooled liquid?
Similar to liquids, glass has a tendency to flow, though very slowly. Therefore, glass is considered as a supercooled liquid. This is the reason that glass windows and doors are slightly thicker at the bottom than at the top.
Exercise Questions
Question 1.1: Define the term 'Amorphous'. Give a few examples of amorphous solids.
Amorphous solids are the solids whose constituent particles are of irregular shapes and have short range order. These solids are isotropic in nature and melt over a range of temperature. Therefore, amorphous solids are sometimes called pseudo solids or supercooled liquids. They do not have definite heat of fusion. When cutting with a sharp-edged tool, they cut into two pieces with irregular surfaces.
Examples: glass, rubber, and plastic.
Question 1.2: What makes a glass different from a solid such as quartz? Under what conditions could quartz be converted into glass?
The arrangement of the constituent particles makes glass different from quartz. In glass, the constituent particles have short-range order, but in quartz, the constituent particles have both long-range and short-range orders.
Quartz can be converted into glass by heating and then cooling it rapidly.
|
361 videos|822 docs|301 tests
|
FAQs on The Solid State - 1 (Old NCERT) NCERT Solutions - Chemistry for JEE Main & Advanced
| 1. What is the Solid State in chemistry? |  |
| 2. What are some examples of Solid State materials? |  |
| 3. What are crystal lattices and how do they relate to Solid State chemistry? |  |
| 4. How is Solid State chemistry related to the NEET exam? |  |
| 5. What are some common applications of Solid State materials in everyday life? |  |