NCERT Solutions Class 11 Maths Chapter 7 - Binomial Theorem
Exercise 7.1
Q1: Expand the expression (1– 2x)5
Ans: By using Binomial Theorem, the expression (1– 2x)5 can be expanded as
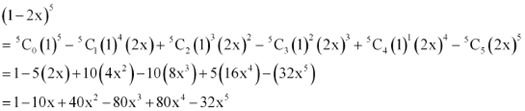
Q2: Expand the expression 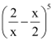
Ans: By using Binomial Theorem, the expression 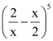 can be expanded as
can be expanded as
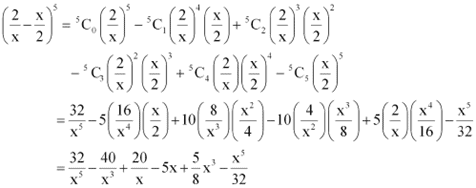
Q3: Expand the expression (2x – 3)6
Ans: By using Binomial Theorem, the expression (2x – 3)6 can be expanded as
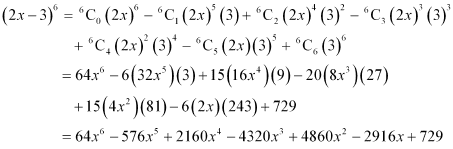
Q4: Expand the expression 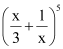
Ans: By using Binomial Theorem, the expression 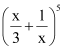 can be expanded as
can be expanded as
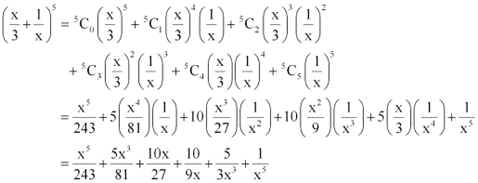
Q5: Expand 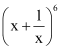
Ans: By using Binomial Theorem, the expression 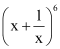 can be expanded as
can be expanded as
Q6: Using Binomial Theorem, evaluate (96)3
Ans: 96 can be expressed as the sum or difference of two numbers whose powers are easier to calculate and then, binomial theorem can be applied.
It can be written that, 96 = 100 – 4
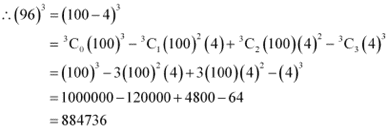
Q7: Using Binomial Theorem, evaluate (102)5
Ans: 102 can be expressed as the sum or difference of two numbers whose powers are easier to calculate and then, Binomial Theorem can be applied.
It can be written that, 102 = 100+ 2
Q8: Using Binomial Theorem, evaluate (101)4
Ans: 101 can be expressed as the sum or difference of two numbers whose powers are easier to calculate and then, Binomial Theorem can be applied.
It can be written that, 101 = 100+ 1
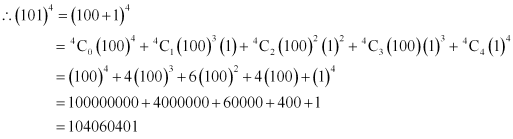
Q9: Using Binomial Theorem, evaluate (99)5
Ans: 99 can be written as the sum or difference of two numbers whose powers are easier to calculate and then, Binomial Theorem can be applied.
It can be written that, 99 = 100 – 1
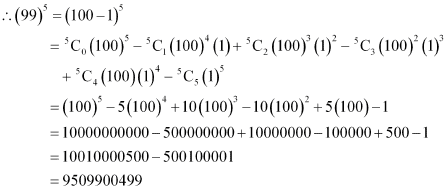
Q10: Using Binomial Theorem, indicate which number is larger (1.1)10000 or 1000.
Ans: By splitting 1.1 and then applying Binomial Theorem, the first few terms of (1.1)10000 can be obtained as
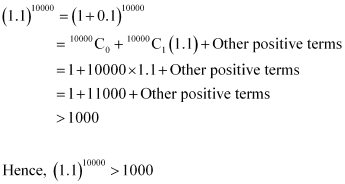
Q11: Find (a + b)4 – (a – b)4. Hence, evaluate 
Ans: Using Binomial Theorem, the expressions, (a + b)4 and (a – b)4, can be expanded as
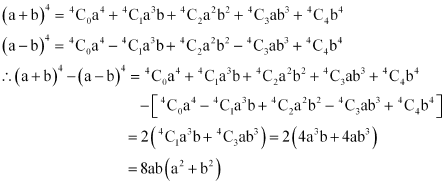
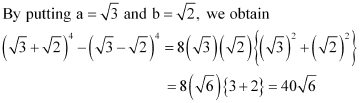
Q12: Find (x + 1)6 + (x – 1)6. Hence or otherwise evaluate  .
.
Ans: Using Binomial Theorem, the expressions, (x + 1)6 and (x – 1)6, can be expanded as
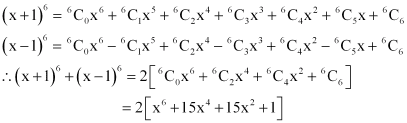
By putting 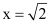 , we obtain
, we obtain
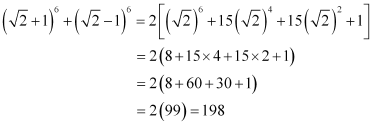
Q13: Show that  is divisible by 64, whenever n is a positive integer.
is divisible by 64, whenever n is a positive integer.
Ans: In order to show that 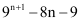 is divisible by 64, it has to be proved that,
is divisible by 64, it has to be proved that, , where k is some natural number
, where k is some natural number
By Binomial Theorem,
For a = 8 and m = n 1, we obtain
Thus,  is divisible by 64, whenever n is a positive integer.
is divisible by 64, whenever n is a positive integer.
Q14: Prove that  .
.
Ans: By Binomial Theorem,
By putting b = 3 and a = 1 in the above equation, we obtain
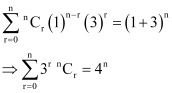
Hence, proved.
Exercise Miscellaneous
Question 1: If a and b are distinct integers, prove that a – b is a factor of an – bn, whenever n is a positive integer.
[Hint: write an = (a – b + b)n and expand]
ANSWER : - In order to prove that (a – b) is a factor of (an – bn), it has to be proved that
an – bn = k (a – b), where k is some natural number
It can be written that, a = a – b + b
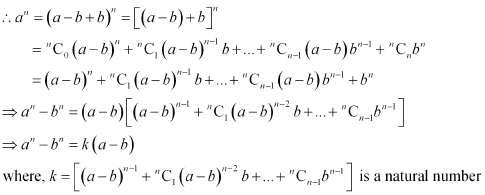
This shows that (a – b) is a factor of (an – bn), where n is a positive integer.
Question 2: Evaluate 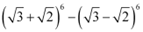 .
.
ANSWER : - Firstly, the expression (a + b)6 – (a – b)6 is simplified by using Binomial Theorem.
This can be done as
Question 3: Find the value of 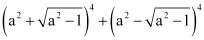 .
.
ANSWER : - Firstly, the expression (x + y)4 (x – y)4 is simplified by using Binomial Theorem.
This can be done as
Question 4: Find an approximation of (0.99)5 using the first three terms of its expansion.
ANSWER : - 0.99 = 1 – 0.01
Thus, the value of (0.99)5 is approximately 0.951.
Question 5: Find n, if the ratio of the fifth term from the beginning to the fifth term from the end in the expansion of 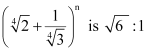
ANSWER : - In the expansion, 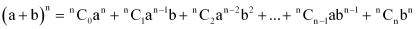 ,
,
Fifth term from the beginning 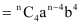
Fifth term from the end 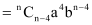
Therefore, it is evident that in the expansion of 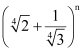 , the fifth term from the beginning is
, the fifth term from the beginning is 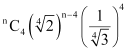 and the fifth term from the end is
and the fifth term from the end is 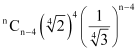 .
.
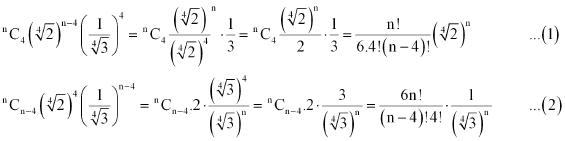
It is given that the ratio of the fifth term from the beginning to the fifth term from the end is 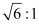 . Therefore, from (1) and (2), we obtain
. Therefore, from (1) and (2), we obtain
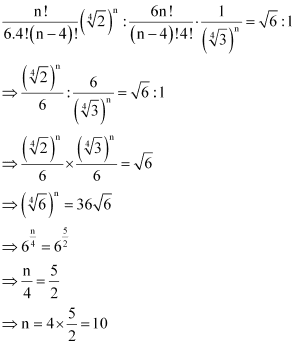
Thus, the value of n is 10.
Question 6: Expand using Binomial Theorem 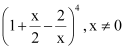 .
.
ANSWER : - Using Binomial Theorem, the given expression  can be expanded as
can be expanded as
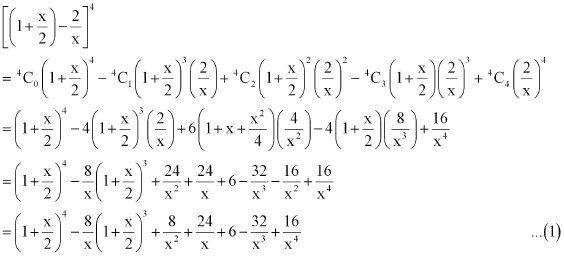
Again by using Binomial Theorem, we obtain
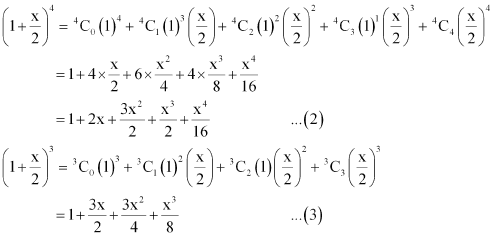
From (1), (2), and (3), we obtain
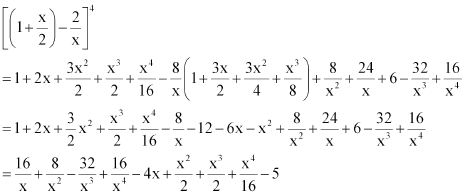
Question 7: Find the expansion of 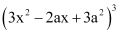 using binomial theorem.
using binomial theorem.
ANSWER : - Using Binomial Theorem, the given expression 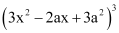 can be expanded as
can be expanded as
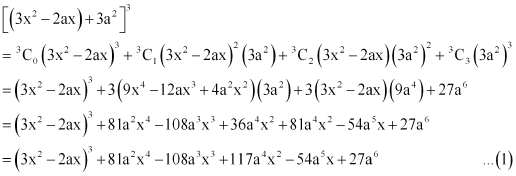
Again by using Binomial Theorem, we obtain
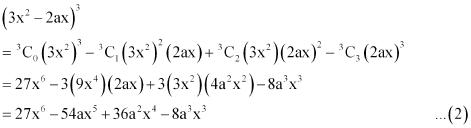
From (1) and (2), we obtain

|
172 videos|503 docs|154 tests
|
FAQs on NCERT Solutions Class 11 Maths Chapter 7 - Binomial Theorem
| 1. What is the Binomial Theorem? |  |
| 2. How is the Binomial Theorem used in mathematics? |  |
| 3. Can the Binomial Theorem be applied to negative exponents? |  |
| 4. What are some real-life applications of the Binomial Theorem? |  |
| 5. How can one remember and apply the Binomial Theorem effectively in exams? |  |

















